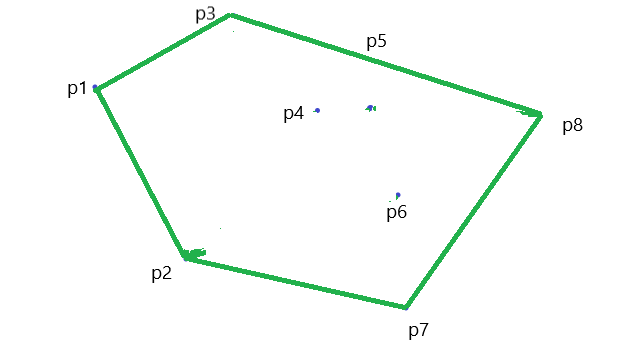
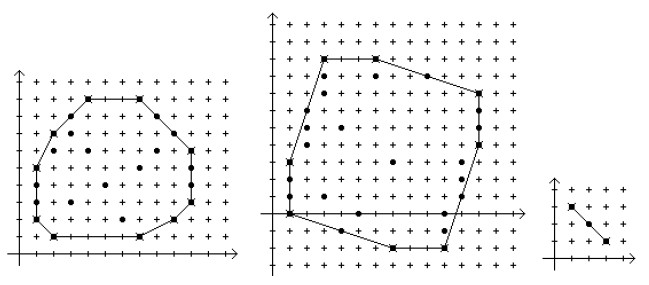
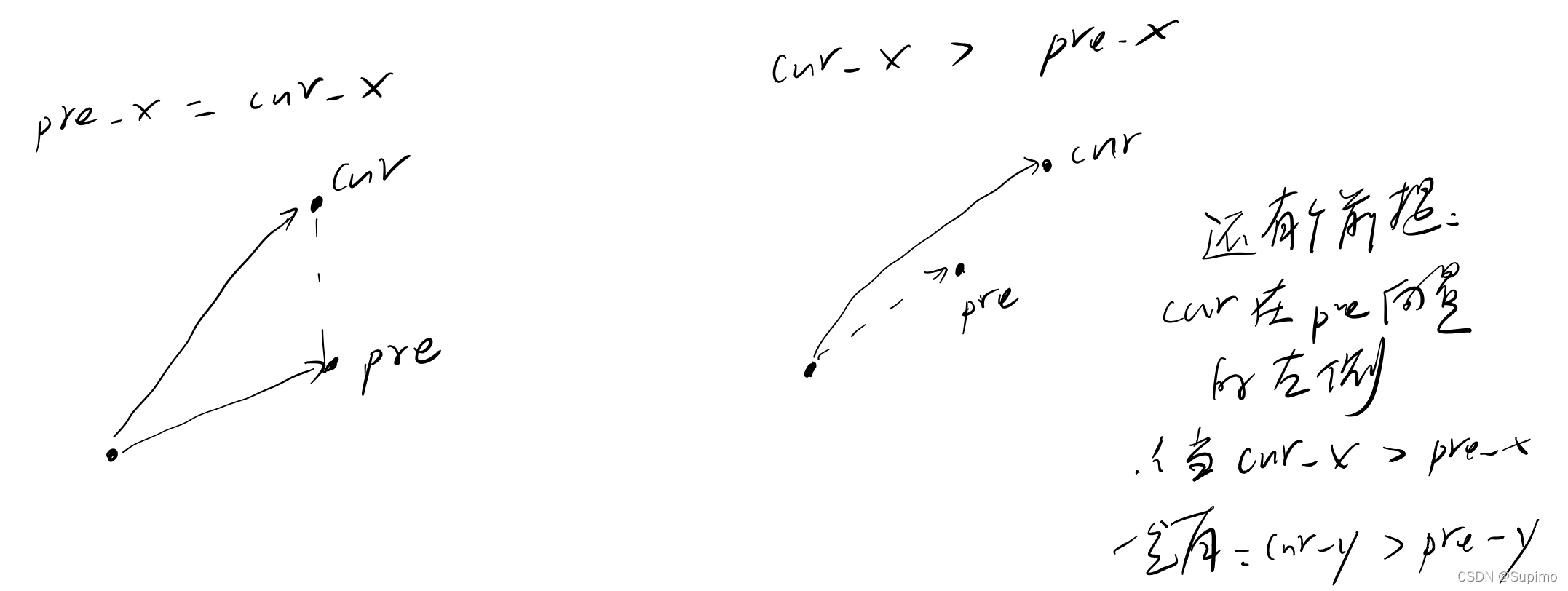假设平面上给出N个点，现在要求过上面的点把所有的点都包起来，并且周长最小，这些点就是凸包上的点。
确定凸包上的点有多种做法，但是只有Graham扫描时间复杂度稳定在nlog(n)上，所以就记录一下这个算法。
**步骤：**
1.找出给定点中最靠近左下方的点
2.通过这个点与其它点连线与水平方向会构成夹角，根据夹角大小进行由小到大排序
3.根据动图中的情况，来说明扫描过程。
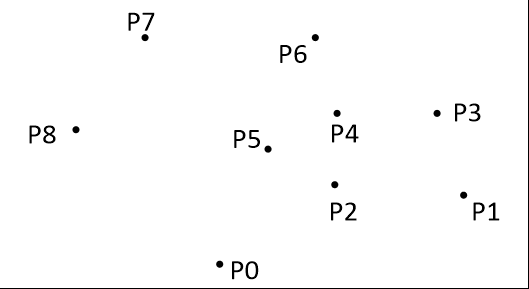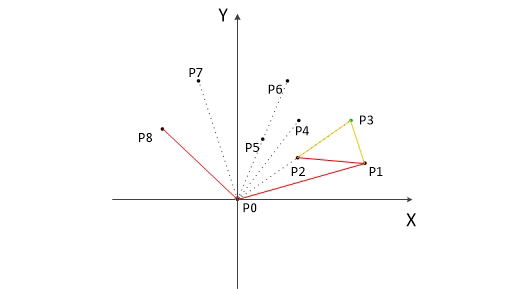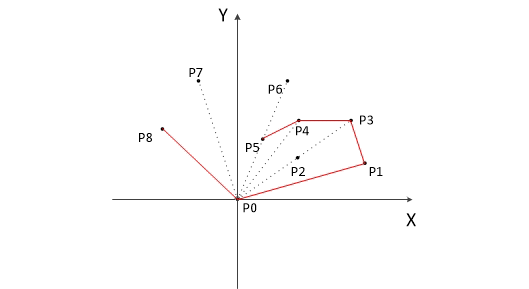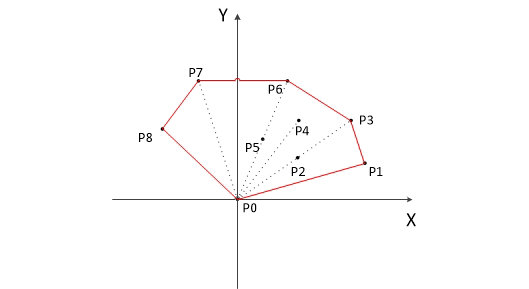Graham扫描过程
凸多边形的边从最左下角点开始，逆时针的相邻三个点P0,P1,P2构成的向量,的夹角都是大于0的。也就是说，针对途中的情况，P2,P4,P5点是不可能在凸包上的。
假设P4在凸包上，那么对于P3,P4,P6来说，,向量的的夹角是小于0的，最后会呈现凹多边形的形态。
以P0,P1,P2,P3,P4,P5,P6来说明确定凸包点的计算方式：
(1)使用栈来存储最终位于凸包上的点的位置。
(2)最开始排好顺序的三个点P0,P1,P2一定能够组成凸多边形,将它们压入栈中S[P2,P1,P0]，并且P1一定在凸包上，现在不确定的就是P2是否真的在凸包上(有内鬼？ ::aru:discovertruth:: )
(3)对于P3来说，我们使用堆栈中第二个元素P1，第一个元素P2，和扫描到的元素P3，进行比较，来确认P2到底是不是凸包上的点。,向量构成的夹角小于0，说明P2一定不在凸包上，所以P2可以排除了，将P2从栈中弹出。P3又有可能是凸包上的点，所以堆栈现在存有S[P3,P1,P0]。
(4)对于P4来说,,向量**(,)**构成的夹角是大于0的，所以P4有可能是凸包上的点。
(5)当前栈中的点S[P4,P3,P1,P0]。对于P5来说,,**(,)**构成的夹角大于0，所以P5有可能是凸包上的点，所以对战现在存有S[P5,P4,P3,P1,P0]。
(6)对于P6来说，,**(,)**构成的夹角小于0，所以P5不可能是凸包上的点。将P5从栈中弹出。栈中元素为S[P4,P3,P1,P0]。再次执行判断,构成的夹角是否小于0，如果仍旧小于0，再将栈中的元素弹出.....直到能够确定P6是凸包上的点。
实际上就是回溯算法。
下面根据上述描述的过程，贴一下java代码的实现。
(这是POJ的1113号题目，题目链接：Wall。POJ用的是jdk1.5 太老了，所以下面的代码编译会报错...扎心)
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.Comparator;
import java.util.LinkedList;
import java.util.StringTokenizer;
public class Main
{
public static void main(String[] args) throws IOException
{
final BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
final int N = Integer.parseInt(st.nextToken());
final int L = Integer.parseInt(st.nextToken());
final int[][] point = new int[N][2];
for (int i = 0; i < N; i++)
{
st = new StringTokenizer(br.readLine());
point[i][0] = Integer.parseInt(st.nextToken());
point[i][1] = Integer.parseInt(st.nextToken());
}
final LinkedList targetPointsPosition = findPoints(point);
double result = 0;
final int size = targetPointsPosition.size();
for (int i = 0; i < size; i++)
{
if (i == size - 1)
{
result += getDistance(
becomeVector(point[targetPointsPosition.get(i)], point[targetPointsPosition.get(0)]));
continue;
}
result += getDistance(
becomeVector(point[targetPointsPosition.get(i)], point[targetPointsPosition.get(i + 1)]));
}
result += 2 * Math.PI * L;
System.out.println(Math.round(result));
}
private static LinkedList findPoints(int[][] point)
{
final int[] targetPointsPosition = new int[point.length];
final int[] leftBottom = getFirstPoint(point);
// 对点进行排序预处理
Arrays.sort(point, new Comparator() {
@Override
public int compare(int[] ints, int[] t1)
{
final int[] o1 = becomeVector(leftBottom, ints);
final int[] o2 = becomeVector(leftBottom, t1);
// 比较角度的结果
final int compareResult = myCompare(leftBottom, ints, t1);
if (compareResult == 0)
{
// 角度相同的时候,将距离P0点近的排在前面
final double dist1Pow = Math.pow(o1[0], 2) + Math.pow(o1[1], 2);
final double dist2Pow = Math.pow(o2[0], 2) + Math.pow(o2[1], 2);
return dist1Pow - dist2Pow > 0 ? 1 : -1;
}
return compareResult;
}
});
// 执行点的扫描
final LinkedList stack = new LinkedList();
stack.push(0);
stack.push(1);
stack.push(2);
// 角度的正负使用向量的sin值,sin在(-Π,0)为负数,(0,Π)为正数----向量的点乘
int[] p0, p1, p2;
int symbolNum;
for (int i = 3; i < point.length; i++)
{
while (true)
{
final int checkPoint = stack.pop();
p0 = point[checkPoint];
p1 = point[stack.peek()];
p2 = point[i];
symbolNum = symbol(p0, p1, p1, p2);
if (symbolNum == 1)
{
stack.push(checkPoint);
break;
}
}
stack.push(i);
}
return stack;
}
private static int[] getFirstPoint(int[][] point)
{
int[] result = new int[]
{ Integer.MAX_VALUE, Integer.MAX_VALUE };
for (final int[] ints : point)
{
if (ints[0] < result[0])
{
result = ints;
} else if (ints[0] == result[0])
{
if (ints[1] < result[1])
{
result = ints;
}
}
}
return result;
}
// 构造向量 private static int[] becomeVector(int[] p0, int[] p1)
{
return new int[]
{ p1[0] - p0[0], p1[1] - p0[1] };
}
// 用于点的排序的比较器
private static int myCompare(int[] p0, int[] p1, int[] p2)
{
final int[] vector01 = becomeVector(p0, p1);
final int[] vector02 = becomeVector(p0, p2);
final double cos01 = vector01[1] / getDistance(vector01);
final double cos02 = vector02[1] / getDistance(vector02);
if (Math.abs(cos01 - cos02) < 1e-6) { return 0; } // cos在[0,Π]单调递减 return cos01 - cos02 > 0 ? -1 : 1;
}
// ,向量夹角---sin---向量叉乘
private static int symbol(int[] p0, int[] p1, int[] p2, int[] p3)
{
final int[] vector01 = becomeVector(p0, p1);
final int[] vector23 = becomeVector(p2, p3);
final int result = vector01[0] * vector23[1] - vector01[1] * vector23[0];
return result >= 0 ? 1 : -1;
}
private static double getDistance(int[] vector)
{
return Math.sqrt(Math.pow(vector[0], 2) + Math.pow(vector[1], 2));
}
}
