凸包

通常上讲
平面上有很多的点, 用一个 皮筋 圈住 这所有的点, 此时这个 皮筋, 就是 这些点的 凸包

数学上讲
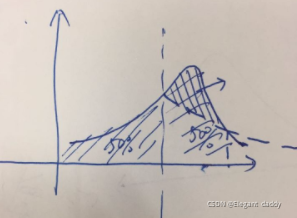
性质1: 凸包上, 任何一条边 他所在的直线 即为L, 则所有的点 都在直线L 的 同一侧

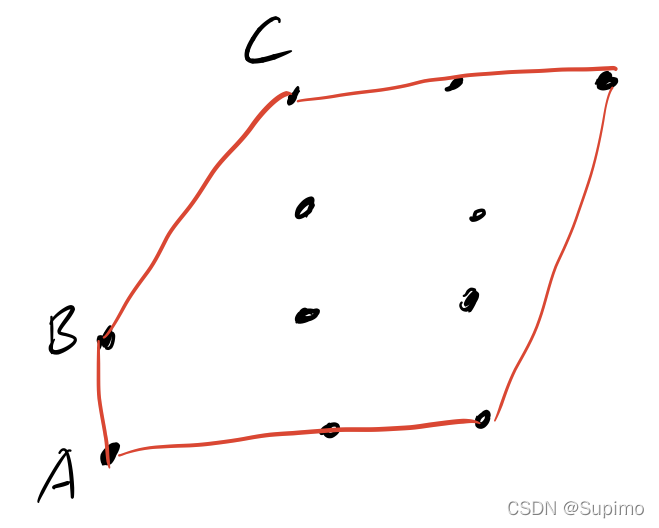
比如以凸包上的 AB边 为例, 所有的点: (要么在AB直线上) (要么都在同一侧比如以A->B这个方向来看, 都在该向量的 右侧)

---

性质2 (重点):

• 由于凸包是一个环, 存在(顺时针 和 逆时针) 两个方向, 不妨先统一规定下 方向, 比如以 顺时针来看.

• 凸包上 任意连续的3个点 ABC, 由于是顺时针, 我们看 A -> B 这个方向的 向量
  你让这个向量, 以 A点 为中心 顺时针的旋转, 直到他 遇到 第一个点 C, 则, 该点C, 就是 继AB后 凸包上的 下一个点

---

性质3: 还是以 顺时针为例

• 对于凸包上的 任意一个点 A (即, 已知, A点 是凸包上的点), 设B点是 A点 顺时针 的 下一个点. 记其他的(除了AB点) 的所有点 为Set集合
  记: A -> B向量 为 vec1, A -> Set 所构成的 所有向量 为 vec2
  则一定有: vec1 * vec2 (叉积) <= 0
• 从上图可以看出, 已知A点 是凸包上的点
  假设C点, 是A点 顺时针的 下一个点;
  但是, 存在B点, 使得: A->C * A->B 的叉积 > 0; 说明: C点, 不是A点的 下一点
  A->B向量 * A->other向量 的叉积 均是 <= 0 的. 说明: B点, 是A点的 下一个凸包上的点

这个性质, 是我们 获取凸包 (即获取凸包上所有的点), 算法的 核心依据.
因为这个性质 告诉我们, 如何通过 一个 凸包上的点, 找到 他的 下一个凸包上的点.

---

算法1 O(n * m)

统一以: 顺时针 为方向

先获取一个凸包上的点Start
O(n)遍历, 找到 对{x,y}sort的 最小/最大的点 无需sort, O(n)cmp即可
这个点, 可以证明, 他一定是凸包上的, 因为他是 极值点;

已知一个凸包上的点A, 如何得到他的下一个点B

Start点;  ' 也就是上面的, 凸包的Start点 '
A点;  ' 已经得到的凸包上的 顺时针的 最后一个点 '
B点 = 任意一个 {非A}的点
FOR( C : 所有点){if( {A->C向量} 是在 {A->B向量} 左侧){B = C;   ' 更新B '}
}
if( B == Start){  ' 这里很重要, 说明 又回到起点了 'break; 
}

具体代码

__VE< int> convex;
convex.clear();
{int j = 0;__FOR(i, 1, n-1, 1){if( -1 == Db_cmp( points[i].x, points[j].x, eps)){j = i;}else if( 0 == Db_cmp( points[i].x, points[j].x, eps) &&-1 == Db_cmp( points[i].y, points[j].x, eps)){j = i;}}convex.__PB( j); ' Start点 '
}while( true){int pre = convex[ convex.size()-1];int cur;__FORC(i, points){if( i != pre){cur = i;break;}}__FORC(i, points){const auto & pa = points[ pre];const auto & pb = points[ cur];Vector2D< double> vec(pa, pb); // 如何把这个double, 自动推导Vector2D< double> nex(pa, points[ i]);if( Db_sign( vec.cross( nex), eps) == 1){cur = i;}}if( cur == convex.at( 0)){break;}else{convex.__PB( cur);}
}

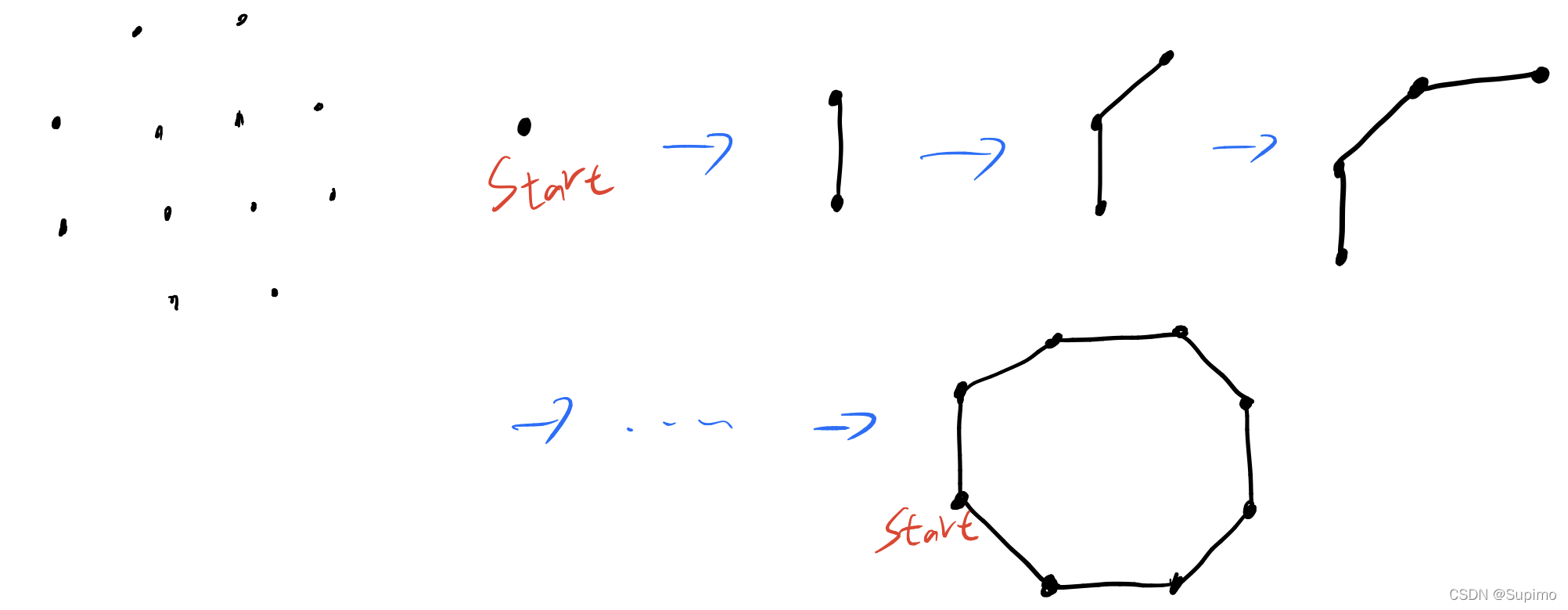
凸包上有多少点, 就会循环多少次. 每次得到一个新的点.

算法2 O(n * logN) Andrew安德鲁算法

对所有点 进行sort后, 令Mi = points.beign(), Ma = points.end()
可以证明, Mi 和 Ma 一定都在 凸包上

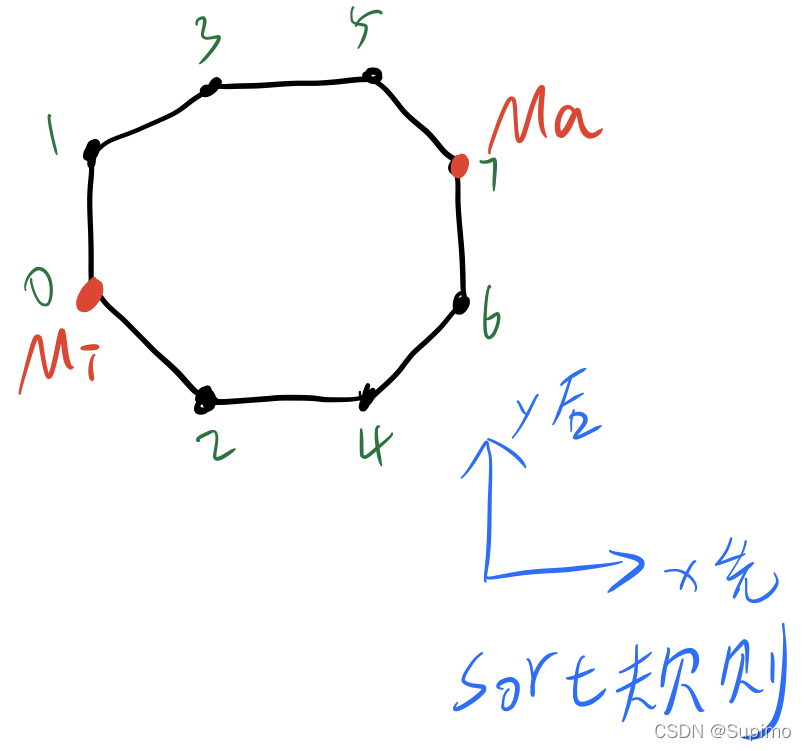
其中绿色的标号, 是将这个点 sort后 的次序.

将这个凸包, 分为 上下两个部分;
一部分是: Mi 1 3 5 Ma 上面的; 一部分是: Mi 2 4 6 Ma 下面的;

---

先求第一部分Mi 1 3 5 Ma:

• 之前的算法是: 求每个点, 都是通过O(n); 即总时间是: O(n * k); 此时, 我们可以做到: O(n), 即一次线性扫描 得到1 3 5这些点

• 以前做法, 做不到 线性; 因为存在这种情况:
  
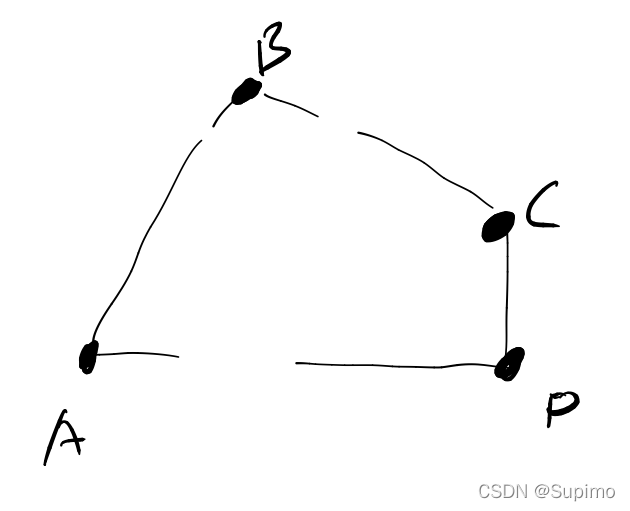
  由于次序是未知的; 比如次序是: A D B C
  当你遍历到D时, 此时凸包是: A D;
  然后遍历到B时, 会 顶替掉 D; 即凸包为: A B
此时, 就不对了 因为, D是凸包上的点; 你给扔掉了; 又因为是线性扫描, D不会再遍历到;

  但是, 很重要的一点是: 在sort后, 不会出现这个问题.
  比如说: (当前点cur) 顶替掉了 (pre点) 即cur向量 在 pre向量 的左侧
  
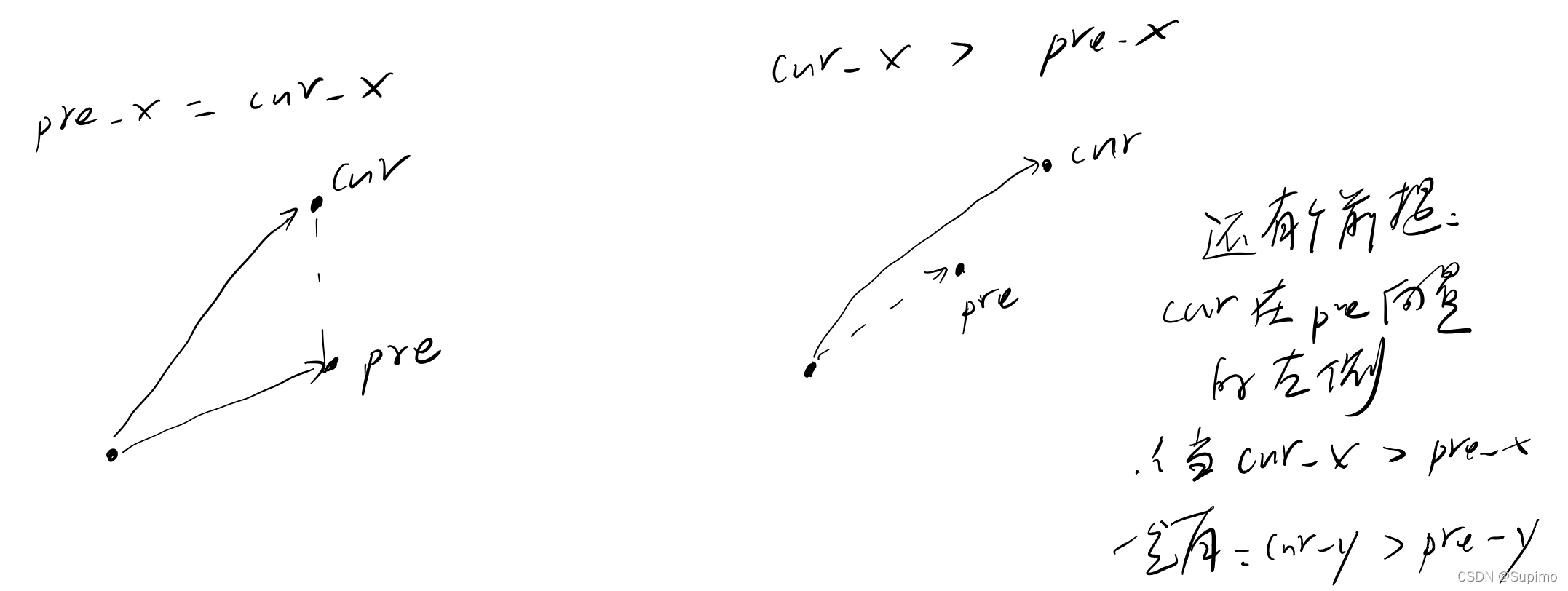
  经分析, 以上两种情况; pre, 都不会是 (当前的 上凸包) 中的
  即, 经过线性扫描, 获取上凸包:

• 在涉及到 "凸包"问题时, 一定要避免 重复点 duplicate!!! 因为, 如果一个向量是零向量, 这是很未知的一种情况.
  即要对点 进行判重; 因为这里已经sort过了, 可以用一个is_duplicate数组来标识;
比如是: [3 3 3] 则第一个3 保留下来, 后面的重复3 就设置为 is_duplicate

• 对 “下凸包”, 他也是 递增的; 上凸包是: mi -> 顺时针 -> ma; 下凸包是: mi -> 逆时针 -> ma;

凸包模板

添加链接描述

sort( points.begin(), points.end());
VE_< bool> is_duplicate( n, false);
{
/// uniqueFOR_(i, 1, n-1, 1){if( points[ i].equal( points[ i-1], eps)){is_duplicate[ i] = true;}}
}VE_< int> obver( n), under( n); // size = capa = n
obver.resize( 0); // size=0, capa = n
under.resize( 0);
{/// obovePB_( obver, 0);FOR_(i, 1, n-1, 1){if( is_duplicate[ i]){continue;}if( obver.size() == 1){PB_( obver, i);}else{while( obver.size() >= 2){const auto & p_beg = points[ ATT_(obver, 1)];const auto & p_end = points[ ATT_(obver, 0)];Vector2D< double> cur( p_beg, p_end);Vector2D< double> nex( p_beg, points[ i]);if( nex.relative( cur, eps) == Direction2D_Left){ ' 顺时针 'obver.pop_back();}else{break;}}PB_( obver, i);}}
}{
/// underPB_( under, 0);FOR_(i, 1, n-1, 1){if( is_duplicate[ i]){continue;}if( under.size() == 1){PB_( under, i);}else{while( under.size() >= 2){const auto & p_beg = points[ ATT_(under, 1)];const auto & p_end = points[ ATT_(under, 0)];Vector2D< double> cur( p_beg, p_end);Vector2D< double> nex( p_beg, points[ i]);if( nex.relative( cur, eps) == Direction2D_Right){ ' 逆时针 'under.pop_back();}else{break;}}PB_( under, i);}}}
double ans = 0;
FOR_(i, 0, obver.size()-2, 1){ans += points[ AT_(obver, i)].distance_to( points[ AT_(obver, i + 1)], eps);
}
FOR_(i, 0, under.size()-2, 1){ans += points[ AT_(under, i)].distance_to( points[ AT_(under, i + 1)], eps);
}