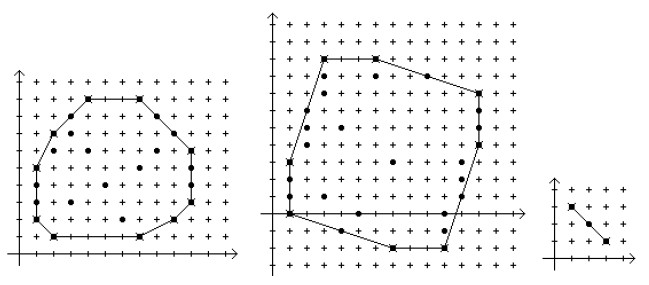
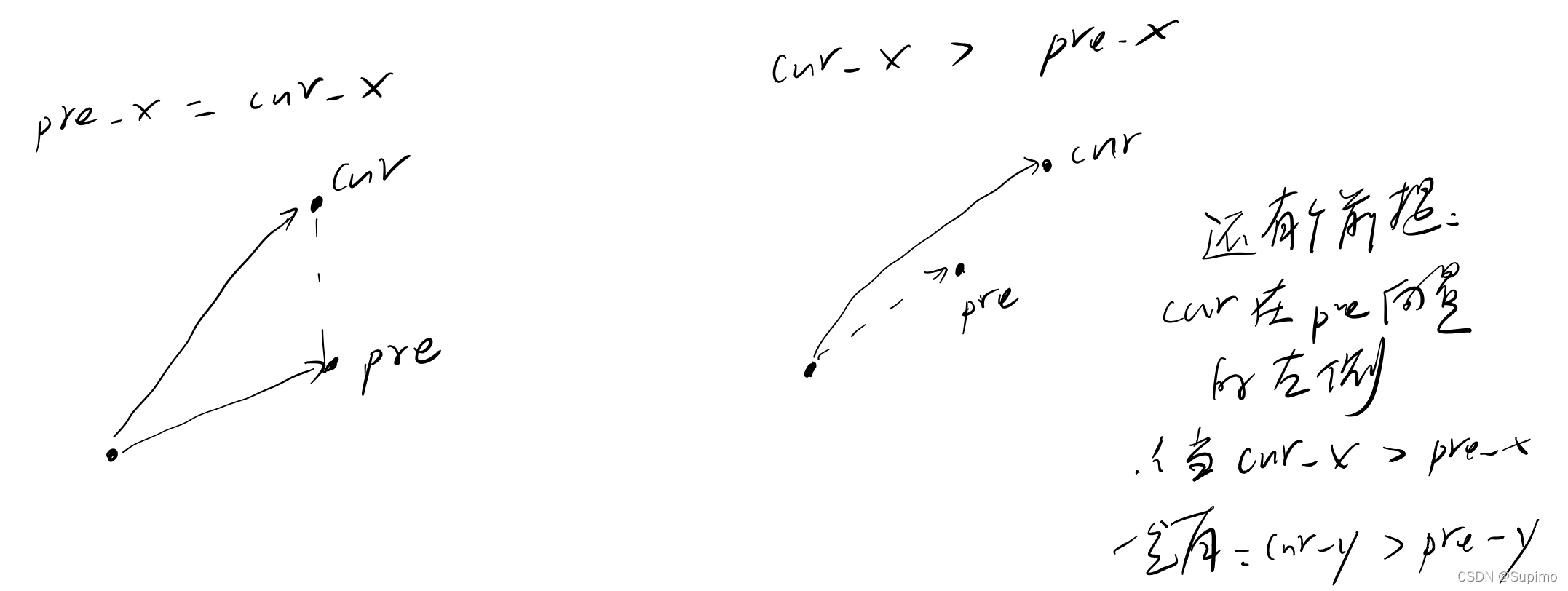首先讲解一下凸包的概念
用比较抽象的说就是:
在一个实数向量空间V中,对于给定集合X,所有包含X的凸集的交集S被称为X的凸包。X的凸包可以用X内所有点
(X1,...Xn)的凸组合来构造.
简单来说:
给你一个点集Q,你可以把Q中的每个点想象成一块木板上的铁钉,而点集Q的凸包就是包围了所有铁钉的一条拉紧
了橡皮绳所构成的形状;
如图:
求凸包可以用Craham扫描法,它用了一种叫"旋转扫除"的技术;
在讲解这个算法之前,我先来介绍几个计算几何概念;
—————————————————————————————————————————
叉积:(在这里只讨论在二维平面的时候)
在二维平面中存在向量p1和p2,他们的叉积等于由向量p1和向量p2构成的平行四边形的面积。
若p1为(x1,y1),p2为(x2,y2);那么p1 * p2 = x1 * y2 - x2 * y1;(注意顺序不能变);
叉积的性质:
1:得到两个向量之间的顺逆关系:
若p1 * p2 >0,则p1在p2的顺时针方向;
若p1 * p2 <0, 则p1在p2的逆时针方向;
若p1 * p2 = 0, 则p1和p2共线(有可能同向,有可能反向);
如上图,p1 * p2 > 0,则p1在p2的顺时针时针方向;
2:确定一个角的转向:
如图有两角<p0p1p2和角<p0p1p2;
为了好区分我们把第一个角叫做<a,第二个角叫<b;
为了判断角的转向,我们需要判断向量p0p1在p0p2的逆时针方向还是顺时针方向(如图)
如果p0p1在p0p2的顺时针方向,则角是向左转,如<a;
如果p0p1在p0p2的逆时针方向,则角是向右装, 如<b;
总结一下就是对于角<p0p1p2,如果p0p1 * p0p2 < 0,则该角向左转;
如果p0p1 * p0p2 > 0,则该角向右转;
注意p0必须在最下面(也就是p0的y坐标必须是三个点中最小的)
基于这个基本的规律我们就能求出一个点集的凸包
以下是求凸包的过程。
————————————————————————————————————
观察凸包我们能发现凸包上的每一个点与它相邻点构成的角都是向左转的;
我们把相邻的左转角连成的不封闭图形叫做凸壳(如下图)
图一,图二是凸壳,图三不是凸壳。
可以看出求凸包的过程就是一个不断维护凸壳的过程。
我们可以借助栈这个结构来维护凸壳。
第一步我们要对这些点按极角的大小进行排序
我们首先选择最左下的那个点作为原点(参照点),之后按极角大小排序,(小的在前)
如果极角相等的话就按距离远近排序,(近的在前);
第二步用栈维护这个凸壳,直到形成一个封闭图形为止;
代码如下:
#include<stdio.h>
#include<algorithm>
#include<math.h>
using namespace std;
const int INF = 50005;struct node
{double x,y;
};node data[INF];node res[INF]; //数组模拟栈(这里如果用stl自带的栈会比较麻烦) double Graham(node* data,node* res, int n);double cross(node a, node b, node mark); //求向量mark->a, 向量mark-> b的叉积;double dis(node a, node b); //求a,b两点距离;long long dis1(node a, node b); bool cmp(node a,node b)
{double ans = cross(a,b,data[0]);if(ans > 0 || (ans == 0 && dis(a,data[0]) < dis(b,data[0]))) return true;return false;
}/*
8
0 0
2 0
4 0
4 2
4 4
2 4
0 4
0 24
0 1
0 2
0 3
0 4*/int main()
{int n;scanf("%d", &n); //点集的大小for(int i = 0; i < n; i++)scanf("%lf %lf",&data[i].x,&data[i].y);int len = Graham(data,res,n); //凸包的大小(也就是凸包所包含点的数目) long long max = -1;for(int i = 0; i <len; i++){printf("%lf %lf\n",res[i].x,res[i].y) ; //输出凸包 }return 0;
}double Graham(node* data,node* res, int n)
{//求出最左下的那个点(原点或参照点),并将此点和data[0]交换一下-------------------------int t = 0;for(int i = 1; i <n; i++){if(data[t].y > data[i].y || (data[t].y == data[i].y) && data[t].x > data[i].x)t = i;} node temp = data[t];data[t] = data[0];data[0] = temp;//将除了data[0]之外的点按与data[0]的极角从小到大排序-----------------------/* 如果用注释的部分来排序会很慢,所以用快排 for(int i = 1; i < n; i++){int t = i;for(int j =i+1; j < n; j++){double flag = cross(data[t],data[j],data[0]);if(flag < 0 || ( flag == 0 && dis(data[t],data[0]) > dis(data[j], data[0]) ) )t = j;}node temp1 = data[t];data[t] = data[i];data[i] = temp1;} */sort(data + 1,data + n,cmp);//初始化栈res----------------------------------------------------------------res[0] = data[0];int top = 0;//利用栈不断维护凸壳---------------------------------------------------------- for(int i = 1; i < n; i++){while(top > 0 && cross(res[top-1], data[i] ,res[top]) >= 0) //找出所有右转的点,然后弹出栈 top--;res[++top] = data[i];}return top + 1;}
double cross(node a, node b, node mark)
{return (a.x - mark.x) * (b.y - mark.y) - (b.x - mark.x) * (a.y - mark.y);
} double dis(node a, node b)
{return sqrt( (a.x -b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y) );
}