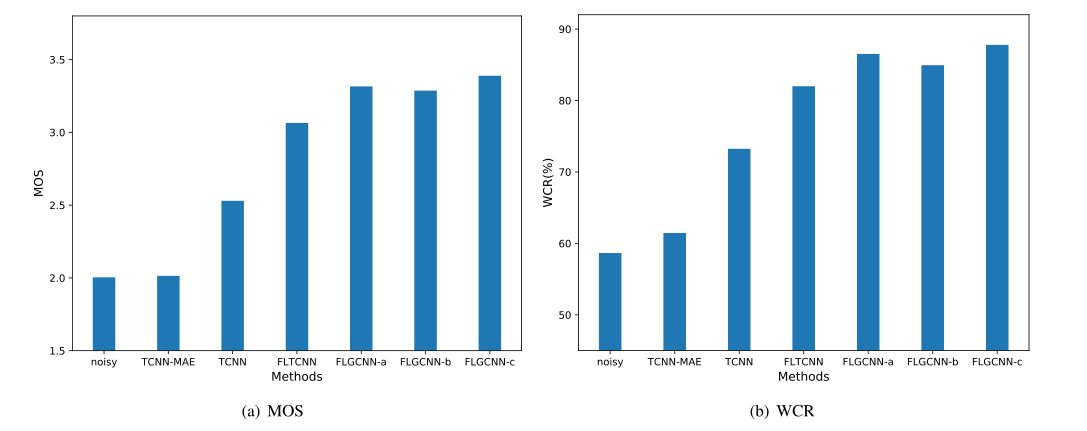
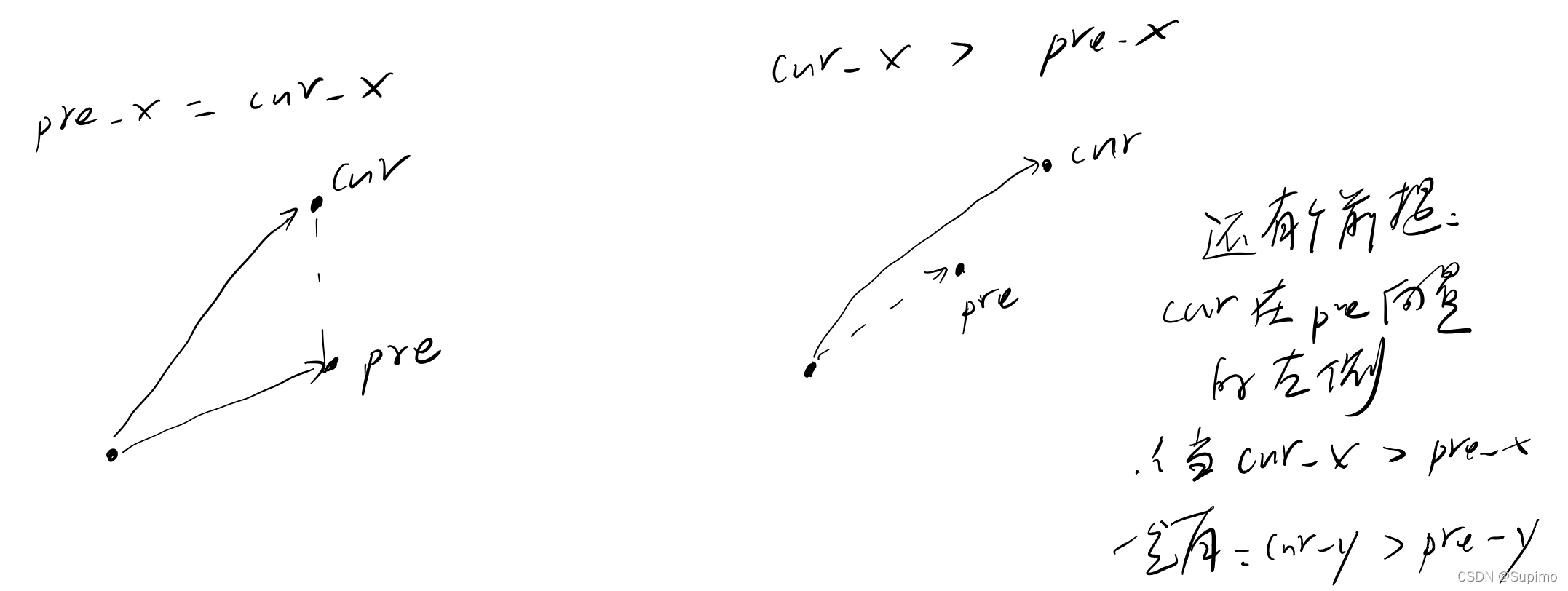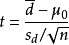一、引言
凸包(Convex Hull)是一个计算几何(图形学)中的概念。
在一个实数向量空间V中,对于给定集合X,所有包含X的凸集的交集S被称为X的凸包。X的凸包可以用X内所有点(X1,...Xn)的凸组合来构造。
通俗来说,如果给定二维平面上的点集,凸包就是将最外层的点连接起来构成的凸多边形,它能包含点集合中所有的点。
下图中外部的5个点就组成了这个点集的一个凸包
可以了解到凸包的一些性质:
1、它包围了点集中所有的点
2、它是凸多边形
二、凸包的求法
介绍一种容易实现的Graham扫描算法。
首先,将所有点按x坐标从小到大排序,对于x相同的,按照y从小到大排序。根据几何知识,排序后第一个点和最后一个点一定是凸包上的点。于是可以根据这两个点将这个凸包分成两部分来求解,分别为上下两条链。求下侧链时,只需将点从小到大逐个加入凸包中并进行检查,每加入一个点后都需要向前验证凸性是否存在(比如上图中的情况);当遍历过所有的点时,既下侧链已完成,然后求上侧链,从最后一个点从大到小逐个加入凸包并验证凸性,注意在求上侧链时,就与下侧链无关,因此可以当成两个独立的链来求解。
分析这个过程中可能出现的难点,就是如何验证凸性,当添加一个新点时,只用判断新点在上条线的左侧还是右侧,无论哪条链,只有新点在左侧时,才满足凸性。如下图这种情况,当新加入点P时,P在向量AB的右侧(从A看向B,既用向量分析),因此不再满足凸性,所以B点一定在凸包内,将B点删去,继续向前判断,可以发现A也不在凸包上,将A点删去,一直向前判断,直到满足凸性为止。
因此判断凸性这个问题就变成了如何判断一个点在一个向量的左侧还是右侧。
可以利用向量的叉积,回忆向量的叉积, 使用右手定则判断叉积结果的正负,右手定则可以和P点与的位置关系结合起来,可以自己画图尝试一下。对于上图,做
和
,如果
结果小于0,那么P就在
的右侧,如果结果大于0,那么P就在左侧,既符合凸性,如果等于0,P就在
方向上。 (判断叉积正负时,有公式
)
//定义 点 的类型
typedef struct{double x, y;
}Point;//计算两个向量叉积
//第一个向量起点a1,终点b1
//第二个向量起点a2,终点b2
double cross(Point a1, Point b1, Point a2, Point b2)
{double x1=b1.x-a1.x;double x2=b2.x-a2.x;double y1=b1.y-a1.y;double y2=b2.y-a2.y;return x1*y2-x2*y1;
}//求点集p的凸包,函数返回值为这个凸包的点集
vector<Point> convex_hull(vector<Point> p, int n)
{sort(p.begin(), p.end(), cmp_x); //按所定的规则给点排序int k=0; //凸包中点的个数vector<Point> q(2*n);int i, t;//求下侧链for (i=0; i<n; i++) //n个点遍历加入凸包并判断凸性{while (k>1 && cross(q[k-1], q[k-2], p[i], q[k-1])<=0)k--; //如果叉积小于等于0,凸包中最新的点出栈q[k++]=p[i];}//求上侧链for (i=n-2, t=k; i>=0; i--){while (k>t && cross(q[k-1], q[k-2], p[i], q[k-1])<=0)k--;q[k++]=p[i];}q.resize(k-1); //重设凸包大小return q;
}//排序的依据
bool cmp_x(Point a, Point b)
{if (a.x!=b.x)return a.x<b.x;return a.y<b.y;
}poj 2187 Beauty Contest
平面上有N个牧场。i号牧场位置为(xi, yi),所有牧场位置不相同。请计算距离最远的两个牧场的距离,输出最远距离的平方。
( 2<=N<=50000 -10000<=xi, yi<=10000 )
首先分析这个题,N的数量很大,如果枚举所有距离找出最大的显然会超时。那么通过分析,最远距离的两个点必定是凸包上的点,因此,只用求出这个点集的凸包,枚举凸包中所有点的距离,就可以在规定时间内完成。
int main()
{int n;scanf("%d", &n);vector<Point> p;int i, j;for (i=0; i<n; i++){Point t;scanf("%lf%lf", &t.x, &t.y);p.push_back(t);}vector<Point> q=convex_hull(p, n); //求凸包double res=0;//枚举凸包中最大距离for (i=0; i<q.size(); i++) for (j=i+1; j<q.size(); j++){res=max(res, dist(q[i], q[j]));}printf("%.0f\n", res);return 0;
}//求距离的平方
double dist(Point p, Point q)
{return (q.x-p.x)*(q.x-p.x)+(q.y-p.y)*(q.y-p.y);
}