参考论文： Broad Learning System: An Effective and Efficient
Incremental Learning System Without
the Need for Deep Architecture

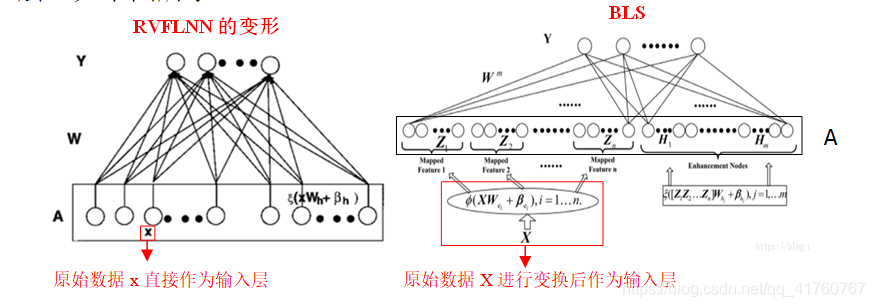
随机向量函数链接网络（RVFLNN）

增强节点

RVFLNN是一个单层网络结构，只有输出层和隐藏层，此外还多余一个增强层。

输入层为训练样本，输入层和增强层之间随机确定一个权值矩阵和偏量，并将增强层与输入层合并作为输入层。

权值计算

对于单层网络来说，我们不需要通过反向传播得到权值，可以直接通过矩阵运算得到$W$，也就是$AW=Y,W=A^{+}Y$，我们只需要得到A的逆即可。

$A$可能并不一定是n*n的的矩阵，因此我们需要得到的是A的伪逆，我们用岭回归的方法求伪逆（Ridge regression），也就是$A^{+}=\underset{\lambda ->0}{\lim }(\lambda I+A{A}^T{)}^{-1}{A}^T$

然而训练样本以及增强层都有可能为了网络结构的性能增加，此时我们希望能够在之前的计算结果上迭代得到新权值，而不是重新对矩阵$A$进行求逆操作，也就是实现增量学习。而实现增量学习的关键在于如何在已知$A_n和A_n^{+}$的情况下，得到$A_{n+1}=A_n|a$（$a$是$A$增强层增加的节点）的伪逆$A_{n+1}^{+}$

Greville 定理

此定理用于解决分块矩阵求伪逆

1. 定理内容
   设$A\in C^{m\ast n}$，记$a_k(k=1,2...n)$为$A$的第$k$列，$A_k$为$A$的前$k$列构成的子矩阵，又记$$d_k=A_{k-1}^{+}{a}_k$$$$c_k=a_k-A_{k-1}{d}_k=a_k-A_{k-1}{A}_{k-1}^{+}{a}_k$$
   则
   $$A_k^{+}=\left[\begin{array}{c}{A}_{k-1}^{+}-d_k{b}^T\\ b^T\end{array}\right]$$
   且$$b^T=\{\begin{array}{l}{c}_k^{+}(c_k\ne 0)\\ (1+d^{T}d{)}^{-1}{d}^T{A}_{k-1}^{+}(c_k=0)\end{array}$$

2. 定理证明
   略

宽度学习系统（Broad Learning System）

数据处理

1. 稀疏自动编码器
   
   我们希望能够提取原先一堆输入中的特征，也就是对原先数据参数进行降维的操作。例如原先输入参数有785个，我们通过sparse autoencoder来使得输入参数降维10个。方法就是构建一个只有一个隐藏层的网络，输入层和输出层都是训练样本。我们只需要得到从输入层到隐藏层的权值矩阵即可。

简单BLS

首先考虑无增量学习的BLS，我们只需要输入参数和特征节点全部放在输入层即可，然后通过岭回归计算得到的权值。

这里唯一需要注意的是特征节点（增强层）权值的设置有两种方法，也就是对于每个节点对应的权值相同或者不同，如下图：


实际上这两种随机权值的设置方法对后面的结果均无影响

增强节点的增量学习

网络结构不可能永远一成不变，我们在得到一个并不满意的结构后，希望能够增加增强层的节点数量来优化我们的网络结构。

由前面增量学习的知识可知，我们不需要重新计算一遍权值的伪逆，只需要在前面的结果上面迭代得到新的伪逆。
对于$A^m=[Z^n|H^m]$，我们有新的$A^{m+1}=[A^m|a]$，由Greville定理可得
$$(A^{m+1}{)}^{+}=\left[\begin{array}{c}{A}^m-d{b}^T\\ b^T\end{array}\right]$$
其中
$$d=(A^m{)}^{+}a$$
$$c=a-A^{m}d$$
$$b^T=\{\begin{array}{l}{c}^{+}(c\ne 0)\\ (1+d^{T}d{)}^{-1}{d}^T{A}_{k-1}^{+}(c=0)\end{array}$$

特征节点的增量学习

除了单独增加增强层节点，我们还有可能需要增加特征值的维度，在这种情况下相当于在mapped feature里增加了一个特征节点

而对于增强层来说，因为mapped feature发生了改变，所以我们不仅仅需要在原先的增强层基础上增加由新的$Z_{n+1}$产生的新节点
并且要增加由$n+1$个mapped feature组成的增强节点。所以一共增加了三个部分：$Z_{n+1}$，为$Z_{n+1}$单独增加的增强节点，将$Z_{n+1}$与原节点合并后的增强节点

输入的增量学习

改变网络结构还有可能是因为输入参数变多了，我们也不希望重新计算一遍权值。在这种情况下与之前的增量学习情况类似，但不同的是我们这次是在矩阵的纵向增加，而非横向。也就是在
$$A_{n+x}^m=\left[\begin{array}{c}{A}_n^m\\ A_x^T\end{array}\right]$$
而
$$(A_{n+x}^m{)}^{+}=[(A_n^m{)}^{+}-B{D}^T|B]$$
其中$D^T=A_x^T(A_n^m{)}^{+}$
$$B^T=\{\begin{array}{l}{C}^{(}C\ne 0)\\ (1+D^{T}D{)}^{-}1(A_n^m)D(C=0)\end{array}$$
其中$C=A_x^T-D^T{A}_n^m$

SVD

首先我们知道对于方阵$A$来说，我们可以将$A$分解为$A=W\sum W^T$，其中$W$是$A$对应特征向量的矩阵，$\sum$是特征值构成对角线的矩阵。

对于非方阵$A_{m\ast n}$而言，我们也希望它有这样的分解，显然有$A^{T}A$和$A{A}^T$为方阵，我们想把$A$分解为$A=U\Sigma V^T$，则显然有
$$\begin{gathered} A{A}^T=U{\Sigma }_1{U}^T \\ {A}^{T}A=V{\Sigma }_2{V}^T \end{gathered}$$
且能够发现${\Sigma }_1=\Sigma {\Sigma }^T,{\Sigma }_2={\Sigma }^T\Sigma$
因此我们能够通过计算方阵$A^{T}A$和$A{A}^T$的特征值和特征向量来得到A的奇异值分解

因此，我们可以在$\Sigma$中选取k个最大的特征值进行$A$的近似处理。注意这里选取的$U_k$和$V_k^T$分别对应的第k个特征值的特征向量

除此之外，左奇异矩阵U可以用于压缩X的行数，右奇异矩阵V可以用于X的降维，也就是PCA主成分分析。

而在BLS中，我们也同样可以采用SVD进行数据的降维简化，论文中分别对mapped feature、enhanced nodes和增量学习中的节点用SVD右矩阵V进行降维处理，简化数据。