忘记密码怎么办？

如果你用的是windows 10系统，一不小心忘记了系统密码，那应该怎么办呢？

这要分2种情况

Windows 10系统有两种账户，

第一种是微软账户，如果是忘记了微软账户的密码，那很简单，直接在微软官网进行密码找回和修改就好咯~

第二种就是本地账户，本地账户的密码如果忘记了其实非常麻烦，只有输入正确的密码才能进入系统，如果真的想不起来，最后的解决办法只能是重装系统，所有资料全没了，十分忧伤~

所以，这件事告诉我们：

最好使用微软账户登录系统

如果用的是本地账户，一定要牢记密码

找个小本本记下来！

如果就是记不住，想给自己来个双保险，

怎么办呢？

你可以选择在设置密码时同步设置安全问题，

设置安全问题，

可以帮助你在忘记密码时登录系统。

如果你在设置 Windows 10 的本地帐户时添加过安全问题，并且你的Windows 10版本不低于 1803，你可以通过回答安全问题重新登录。

如何设置？

请选择【设置】——【账户】——【登录选项】——【密码】——【更新安全问题】，可以直接参考下图

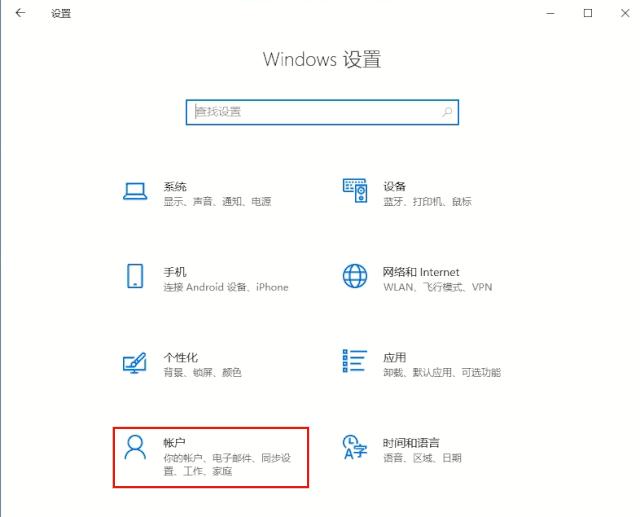
设置好后，如果下次登录时忘记了密码：

在登录屏幕选择“重置密码”

回答安全问题

输入新密码

使用新密码正常登录

就可以啦~

如果没有设置安全问题

或者版本在1803之前

忘记了本地账户密码

怎么办？？？

对于低于 Windows 10 版本 1803 的版本，不存在安全问题。你可以重置自己的设备以选择新密码，但此选项将永久删除你的数据、程序和设置。

若要重置设备(这将永久删除数据、程序和设置)，请执行以下操作：

按住 Shift 键的同时，依次选择屏幕右下角的“电源” 按钮 >“重启”。

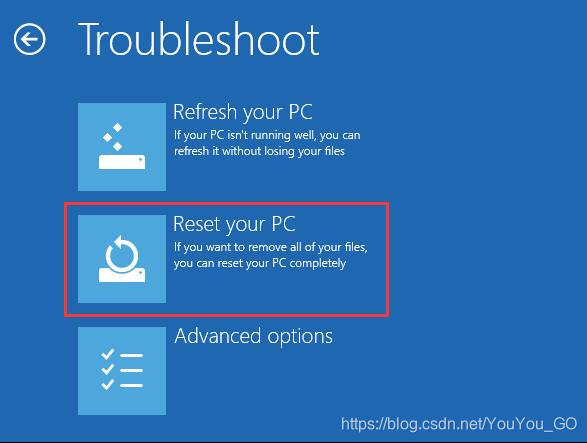
在“选择一个选项”屏幕上，依次选择“疑难解答”>“重置此电脑”。

选择“删除所有内容”。

课代表来帮忙总结：

最好使用微软账户登录

如果使用本地账户，请确保更新系统至1803版本以上，并设置安全问题

及时备份重要的数据，把密码记下来，存在多个地方