蓝桥杯试题算法训练 24点 C++ 详解

问题描述：

　　24点游戏是一个非常有意思的游戏，很流行，玩法很简单：给你4张牌，每张牌上有数字（其中A代表1，J代表11，Q代表12，K代表13），你可以利用数学中的加、减、乘、除以及括号想办法得到24，例如：
　　((A*K)-J)*Q等价于((1*13)-11)*12=24
　　加减乘不用多说了，但除法必须满足能整除才能除！这样有一些是得不到24点的，所以这里只要求求出不超过24的最大值。

输入格式：

　　输入第一行N(1<=N<=5)表示有N组测试数据。每组测试数据输入4行，每行一个整数(1到13)表示牌值。

输出格式：

　　每组测试数据输出一个整数，表示所能得到的最大的不超过24的值。

样例输入：

3
3
3
3
3
1
1
1
1
12
5
13
1

样例输出：

24
4
21

前言：

参考解法：

蓝桥杯算法训练 24点_陆小路-1的博客-CSDN博客

原博客讲得很详细，评论区也有不少问题解答。

(仅需解法的同学/读者直接跳转即可）

这里我还是只讲一下我的解题过程（主要是错误的原因）。

临近省赛，这篇文章就再小小总结一下目前做过的《算法训练》题目。

(删了一大段感慨的话)

笔者，也是要去刷一刷官网的真题才行……

开始：

题做到这里，相信大家已经对一些算法(dp,dfs)有了一定的了解。

已经做过的题目：

《印章》：dp(动态规划)，最终结果由上一步结果推导出。

《拿金币》：同上。

《无聊的逗》：经典的dfs算法。

《礼物》：找规律。

《跳马》：dfs(深度优先搜索), bfs(宽度优先搜索) 都能解。

《数的潜能》：找规律。

《娜神平衡》：dfs + dp?

《粘木棍》：dfs

《车的放置》：dfs

《24点》：dfs

其中，《印章》《拿金币》《礼物》《数的潜能》就不讲了，随机应变吧。

笔者浅浅总结一下这些题所用dfs的区别。

《无聊的逗》，经典的dfs，利用每层递归的三种操作，遍历出所有的情况。但仅限于对当前"对象"进行操作。

《跳马》，经典的dfs，利用每层递归的两种操作，遍历出所有的情况。但也仅限于对当前"对象"进行操作。

《娜神平衡》，同为dfs操作，但它却可以实现：对一些对象进行选择（每层内部都有一个for循环遍历所有对象）。不难发现，其依据是用int或bool数组存放对象的状态。

《粘木棍》，……

《车的放置》，……

《24点》，而本题的dfs操作又有不同，它是每层循环都挑出两个数，对齐进行（加减乘除）。

笔者水平有限，对这些dfs的总结为：

橙色dfs的作用：对某个对象进行不同的操作，适用于穷举"按顺序"的所有情况。

例：给定ABCDEFG……不同的物品，每个物品都可以拿或不拿，请穷举所有情况。

黄色dfs的作用：对某个对象进行不同的操作，适用于穷举"不按顺序"的所有情况。

例：给定ABCDEFG……不同的物品，请穷举所有组合(ABCDEGF……)。

绿色dfs的作用：对两个对象进行不同的操作，适用于穷举"两两配对?"的所有情况。

其实跟黄色dfs差不多，，，

接下来看题，其本质就是问：对4个数进行加减乘除的操作，怎么得到小于等于24最大的数？

一开始我是延续上几题《娜神平衡》的dfs想法，但提交程序后正确率最高只有60%。

上网查了以后发现存在优先级和分配律的问题，

按自己的方式，笔者写的检查错误的代码如下：

#include<iostream>
using namespace std;//分组数量
int N = 0;//数据：最多5组，每组4个
int Date[5][4] = { 0 };//标记数据状态：false：未被使用；true：已使用
int Date_index[5][4] = { 0 };int result[6] = { 0 };//检查数据是否"全部"都已使用 - 作为边界条件
bool func01(int row)
{for (int i = 0; i < 4; i++){if (!Date_index[row][i])return false;}return true;
}//将数字转"字符"返回
string func02(int sum)
{string s = "";do{s += '0' + sum % 10;sum /= 10;} while (sum > 0);reverse(s.begin(), s.end());return s;
}string S;void func(const int row, int sum = 0, bool bol = false, string s = "", int x = 0)
{x++;//若结果已为最大值，无需继续if (result[row] == 24)return;//该row组数据全部用上 - (更新)结束if (func01(row)){s += " = " + func02(sum);if (result[row] < sum && sum <= 24){result[row] = sum;S = s;}return;}//第一次调用时，填充任一数字作为第一位(防止存在0 * 0导致莫名去除了一些数据)if (!bol){for (int i = 0; i < 4; i++){sum = Date[row][i];Date_index[row][i] = x;//标记已使用s = func02(Date[row][i]);func(row, sum, true, s, x);Date_index[row][i] = 0;//回溯}}//第二/三/四次调用else{for (int i = 0; i < 4; i++){if (!Date_index[row][i]){Date_index[row][i] = x;//标记已使用string temp;int x1 = sum + Date[row][i];//加temp = s + " + " + func02(Date[row][i]);func(row, x1, true, temp, x);int x2 = sum - Date[row][i];//减temp = "|" + s + " - " + func02(Date[row][i]) + "|";x2 = x2 > 0 ? x2 : -x2;func(row, x2, true, temp, x);int x3 = sum * Date[row][i];//乘temp = "(" + s + ")" + " * " + func02(Date[row][i]);func(row, x3, true, temp, x);if (Date[row][i] != 0 && sum % Date[row][i] == 0){temp = "(" + s + ")" + " / " + func02(Date[row][i]);func(row, sum / Date[row][i], true, temp, x);//除}else if (sum != 0 && Date[row][i] % sum == 0){temp = func02(Date[row][i]) + " / " + "(" + s + ")";func(row, Date[row][i] / sum, true, temp, x);//除}Date_index[row][i] = 0;//回溯}}}
}int n = 1;//n组测试数据 
int nums[4];//4个数字 
int ans;//不超过24的最大值 //函数功能： 在有n个数的数组nums中	寻找最大的不超过24的值。
void f(int nums[], int n) {//只有1个数时，比较最大值 if (n == 1) {//如果该数不大于24，更新最大值 if (nums[n - 1] <= 24) {ans = ans < nums[n - 1] ? nums[n - 1] : ans;}return;}//遍历两个数的组合 for (int i = 0; i < n - 1; i++) {for (int j = i + 1; j < n; j++) {int a = nums[i], b = nums[j];nums[j] = a + b;		//加法和乘法具有交换律 nums[i] = nums[n - 1];f(nums, n - 1);nums[j] = a * b;nums[i] = nums[n - 1];f(nums, n - 1);nums[j] = a - b;		//减法和除法不具有交换律 nums[i] = nums[n - 1];f(nums, n - 1);nums[j] = b - a;nums[i] = nums[n - 1];f(nums, n - 1);if (b != 0 && a % b == 0) {		//除数不能为0 nums[j] = a / b;nums[i] = nums[n - 1];f(nums, n - 1);}if (a != 0 && b % a == 0) {nums[j] = b / a;nums[i] = nums[n - 1];f(nums, n - 1);}nums[i] = a;    //恢复现场 nums[j] = b;}}
}int main()
{输入数据//cin >> N;//for (int i = 0; i < N; i++)//	for (int j = 0; j < 4; j++)//	{//		cin >> Date[i][j];//	}对每层进行运算//for (int i = 0; i < N; i++)//	func(i);输出结果//for (int i = 0; i < N; i++)//	cout//	<< S << endl//	//<< result[i] << endl//	;int cnt = 0;for (int a = 1; a <= 13; a++){for (int b = a; b <= 13; b++){for (int c = b; c <= 13; c++){for (int d = c; d <= 13; d++){Date[0][0] = a;Date[0][1] = b;Date[0][2] = c;Date[0][3] = d;func(0);cout << S << endl;ans = 0;nums[0] = a;nums[1] = b;nums[2] = c;nums[3] = d;f(nums, 4);cout << " -> " << ans << endl;if (ans != result[0])system("pause>nul");S = "";result[0] = 0;cnt++;}}}}cout << cnt << endl;return 0;
}

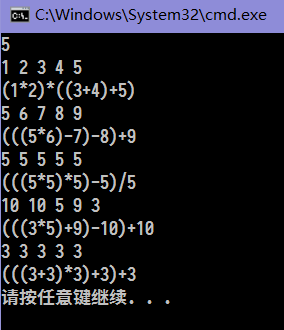
部分运行截图如下：