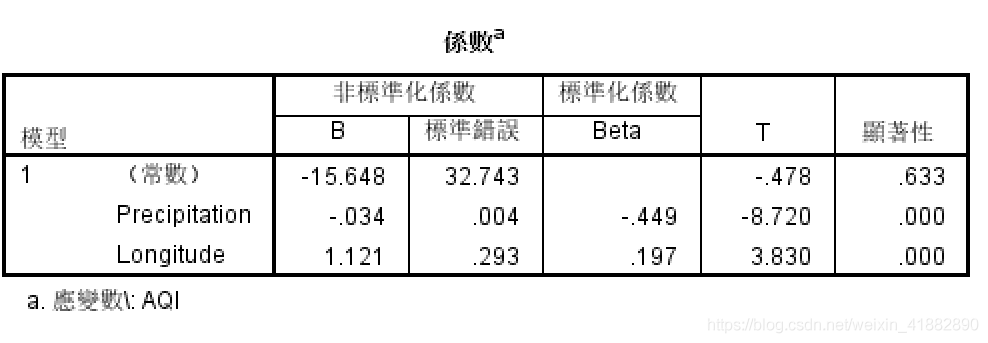
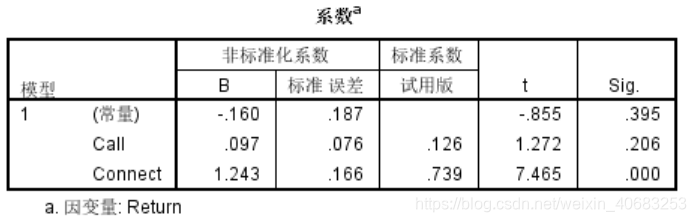
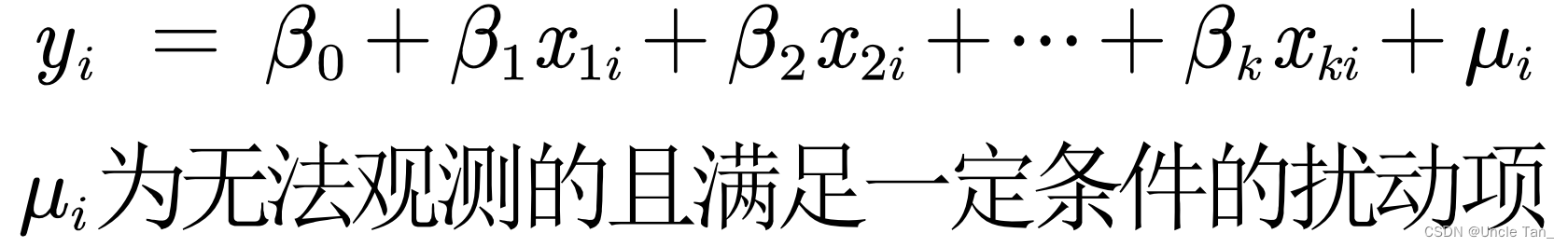基于Python的多元线性回归分析

article/2025/8/28 10:20:16

一、多元线性回归分析（Multiple regression）

1.与简单线性回归相比较，具有多个自变量x

2.多元回归模型

$y=\beta _{0}+\beta _{1}x_{1}+\beta _{2}x_{2}+...+\beta _{n}x_{n}+\varepsilon$

其中 $\varepsilon$ 是误差值，与简单线性回归分析中的要求特点相一致。其余的系数和截距为参数。

3.多元回归方程

$E(y)=\beta _{0}+\beta _{1}x_{1}+\beta _{2}x_{2}+...+\beta _{n}x_{n}$

4.估计多元回归方程(点估计)

$\hat{y}=b_{0}+b _{1}x_{1}+b_{2}x_{2}+...+b _{n}x_{n}$

5.估计方法

使方差和最小，即 $min\sum (y_{i}-\hat{y_{t}})^{2}$

从而得到一个唯一的超平面。

二、自变量里没有类别数据的实例

2.1数据：

100,4,9.3
50,3,4.8
100,4,8.9
100,2,6.5
50,2,4.2
80,2,6.2
75,3,7.4
65,4,6
90,3,7.6
90,2,6.1

2.2代码

from numpy import genfromtxt #将导入的数据转换为numparry（即SK包中可以进行运算的矩阵类型的数据）
from sklearn import linear_model#SK包里的数据集和线性模型
import numpy as np
dataPath = r"Delivery.csv"#r后面的内容默认为一个完整的字符串，忽略里面的\
deliveryData = genfromtxt(dataPath,delimiter=',')print("data")#将已经输入的数据打印出来查看
print(deliveryData)x= deliveryData[:,:-1]#提取所有的行和除倒数第一列之外的所有的列
y = deliveryData[:,-1]#提取所有行和最后一列的数据print(x)#打印x的数据
print(y)#打印y的数据lr = linear_model.LinearRegression()#定义一个模型变量名lr，调用sklearn包中线性模型线性回归分析方法
lr.fit(x, y)#利用上述模型对lr中的x,y数据进行建模print(lr)print("coefficients:")
print(lr.coef_)#获取到的截面的参数值print("intercept:")
print(lr.intercept_)#获取到的截距的参数值xPredict = np.array([102,5]).reshape(1,-1)
yPredict = lr.predict(xPredict)#对所给出的x的预测值进行预测
print("predict:")
print(yPredict)#打印预测的结果

运行结果：

data
[[100.    4.    9.3][ 50.    3.    4.8][100.    4.    8.9][100.    2.    6.5][ 50.    2.    4.2][ 80.    2.    6.2][ 75.    3.    7.4][ 65.    4.    6. ][ 90.    3.    7.6][ 90.    2.    6.1]]
[[100.   4.][ 50.   3.][100.   4.][100.   2.][ 50.   2.][ 80.   2.][ 75.   3.][ 65.   4.][ 90.   3.][ 90.   2.]]
[9.3 4.8 8.9 6.5 4.2 6.2 7.4 6.  7.6 6.1]
LinearRegression()
coefficients:
[0.0611346  0.92342537]
intercept:
-0.8687014667817126
predict:
[9.98415444]Process finished with exit code 0

三、自变量中含有类别型的数据

3.1数据

100,4,0,1,0,9.3
50,3,1,0,0,4.8
100,4,0,1,0,8.9
100,2,0,0,1,6.5
50,2,0,0,1,4.2
80,2,0,1,0,6.2
75,3,0,1,0,7.4
65,4,1,0,0,6
90,3,1,0,0,7.6
90,2,0,0,1,6.1

3.2代码

from numpy import genfromtxt #将导入的数据转换为numparry（即SK包中可以进行运算的矩阵类型的数据）
import numpy as np
from sklearn import linear_model #SK包里的数据集和线性模型datapath=r"Delivery_Dummy.csv" #r后面的内容默认为一个完整的字符串，忽略里面的\
deliveryData = genfromtxt(datapath,delimiter=",")x = deliveryData[1:,:-1]#提取所有的行和除倒数第一列之外的所有的列
y = deliveryData[1:,-1]#提取所有行和最后一列的数据
print(x)
print(y)mlr = linear_model.LinearRegression()#定义一个模型变量名lr，调用sklearn包中线性模型线性回归分析方法mlr.fit(x, y)#利用上述模型对lr中的x,y数据进行建模print(mlr)
print("coef:")
print(mlr.coef_)#获取到的截面的参数值
print("intercept")
print(mlr.intercept_)#获取到的截距的参数值xPredict = np.array([90,2,0,0,1]).reshape(1,-1)
yPredict = mlr.predict(xPredict)#对所给出的x的预测值进行预测print("predict:")
print(yPredict)#打印预测的结果

运行结果：

[[ 50.   3.   1.   0.   0.][100.   4.   0.   1.   0.][100.   2.   0.   0.   1.][ 50.   2.   0.   0.   1.][ 80.   2.   0.   1.   0.][ 75.   3.   0.   1.   0.][ 65.   4.   1.   0.   0.][ 90.   3.   1.   0.   0.][ 90.   2.   0.   0.   1.]]
[4.8 8.9 6.5 4.2 6.2 7.4 6.  7.6 6.1]
LinearRegression()
coef:
[ 0.05446701  0.62208122 -0.10896785  0.5572758  -0.44830795]
intercept
0.44678510998308685
predict:
[6.14467005]Process finished with exit code 0