RRT算法

article/2025/10/4 11:26:15

简介

RRT 算法（快速扩展随机树，rapidly exploring random tree）是一种随机性算法，它可以直接应用于非完整约束系统的规划，不需进行路径转换，所以它的算法复杂度较小，尤为适用于高维多自由度的系统。

缺点是得到的路径质量不是很好。需要后处理进一步优化。
思想是快速扩张一群像树一样的路径以探索（填充）空间的大部分区域，伺机找到可行的路径。

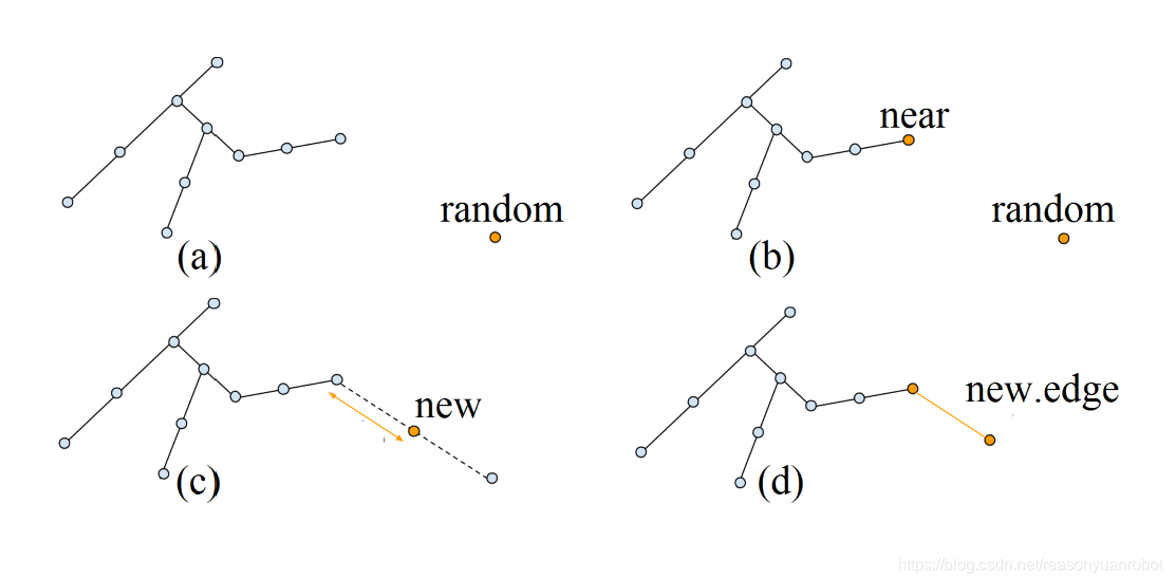
RRT 的基本步骤是：
　　1. 起点作为一颗种子，从它开始生长枝丫；
　　2. 在机器人的“构型”空间中，生成一个随机点X；
　　3. 在树上找到距离X最近的那个点，记为Y吧；
　　4. 朝着X的方向生长，如果没有碰到障碍物就把生长后的树枝和端点添加到树上，返回 2；

åç»´ç©ºé´

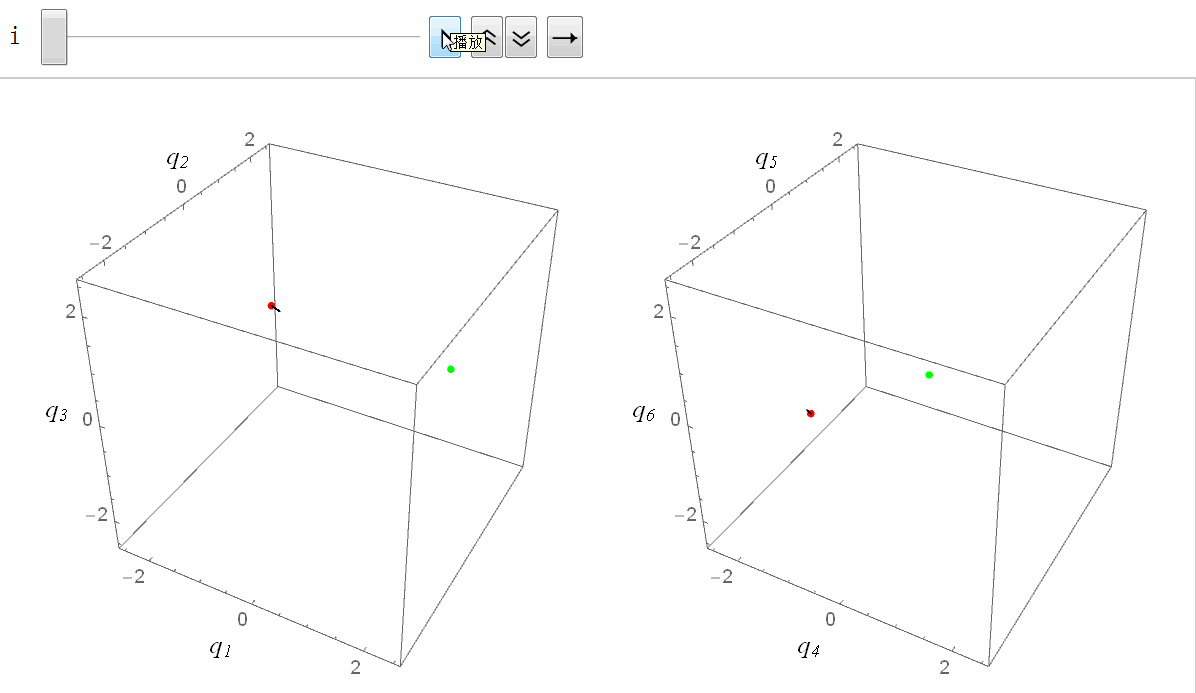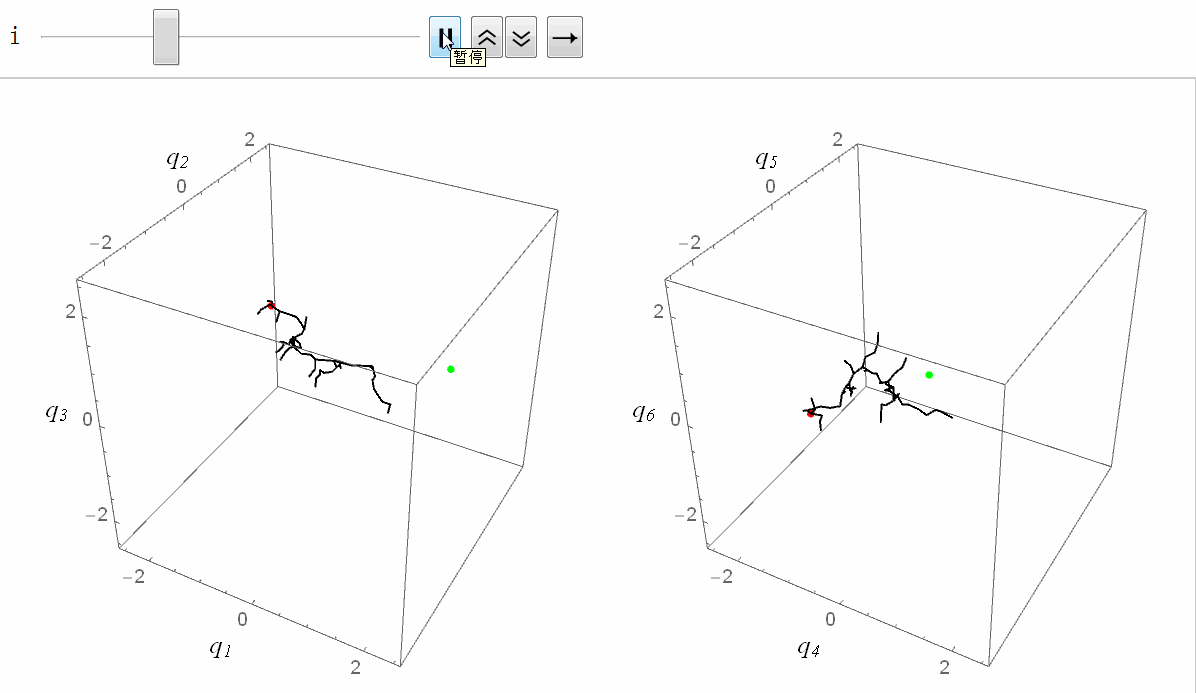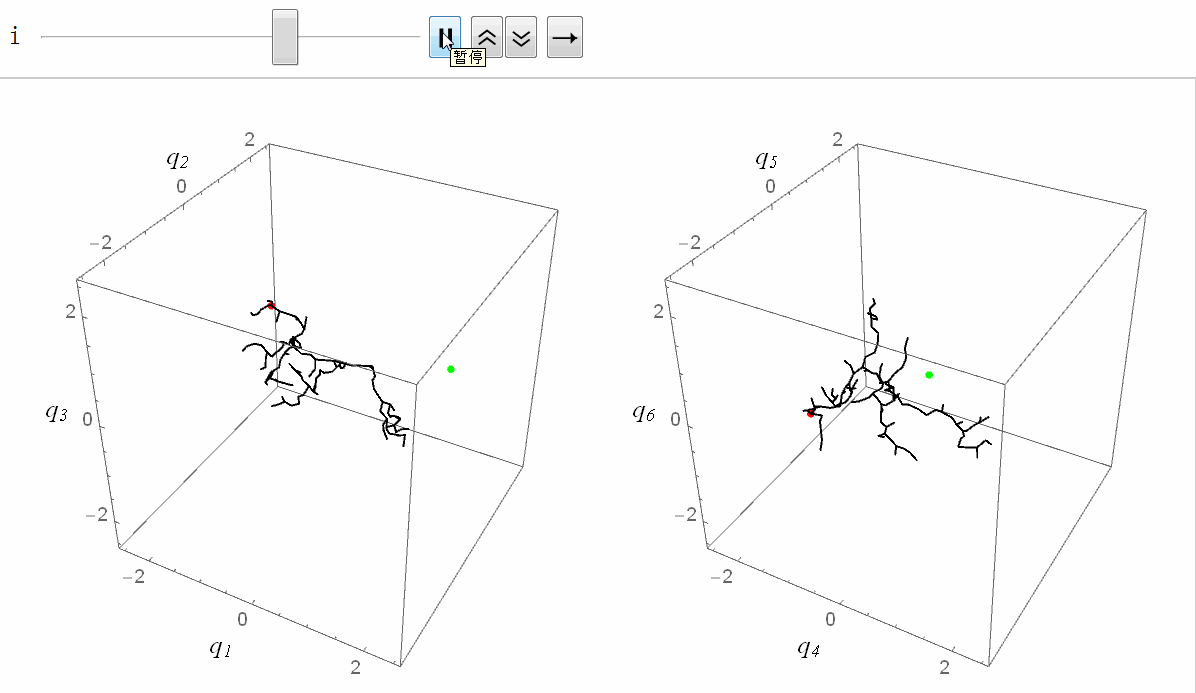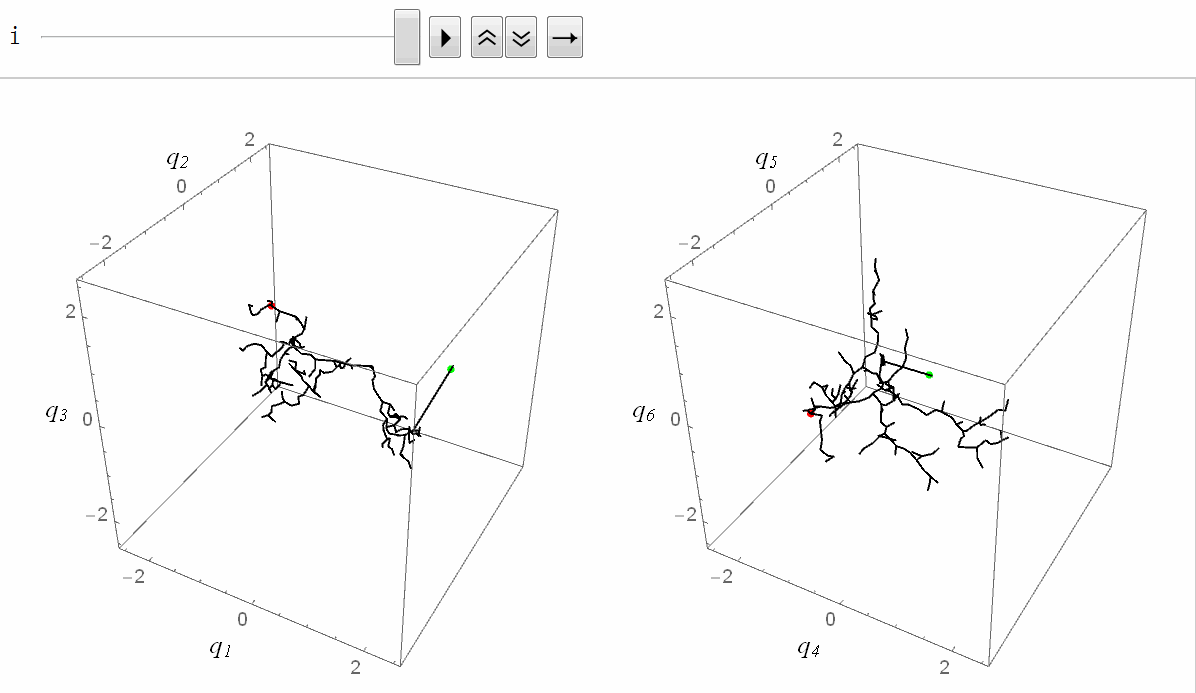
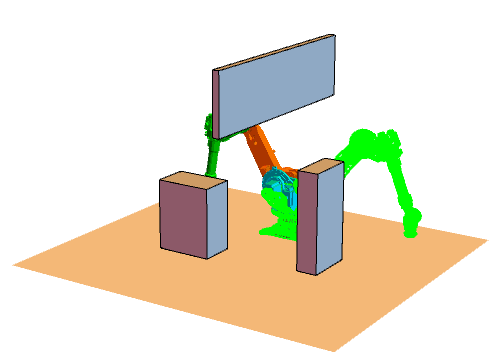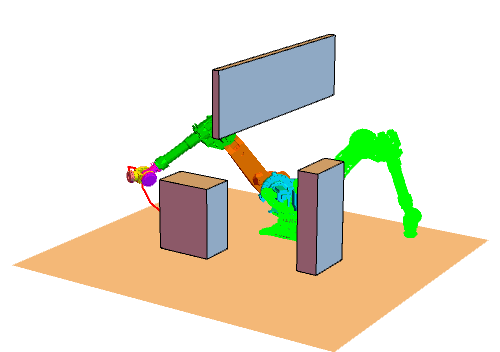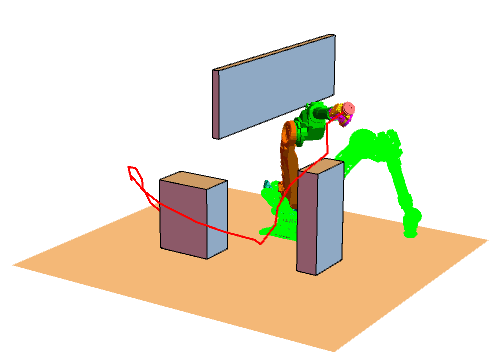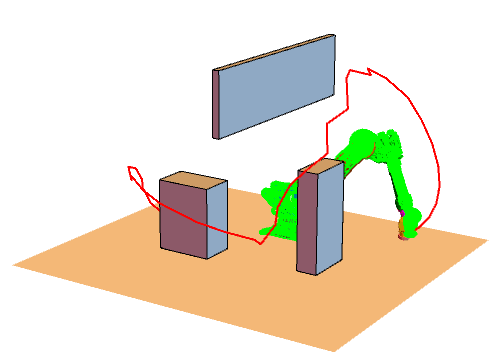
　六维空间的RRT

实际效果如图。

伪代码


function BuildRRT(qinit, K, Δq)T.init(qinit)for k = 1 to Kqrand = Sample()  -- chooses a random configurationqnearest = Nearest(T, qrand) -- selects the node in the RRT tree that is closest to qrandif  Distance(qnearest, qgoal) < Threshold thenreturn trueqnew = Extend(qnearest, qrand, Δq)  -- moving from qnearest an incremental distance in the direction of qrandif qnew ≠ NULL thenT.AddNode(qnew)return falsefunction Sample() -- Alternatively,one could replace Sample with SampleFree(by using a collision detection algorithm to reject samples in C_obstaclep = Random(0, 1.0)if 0 < p < Prob thenreturn qgoalelseif Prob < p < 1.0 thenreturn RandomNode()

初始化时随机树T只包含一个节点：根节点qinit。首先Sample函数从状态空间中随机选择一个采样点qrand（4行）；

然后Nearest函数从随机树中选择一个距离qrand最近的节点qnearest（5行）；

最后Extend函数通过从qnearest向qrand扩展一段距离，得到一个新的节点qnew（8行）。如果qnew与障碍物发生碰撞，则Extend函数返回空，放弃这次生长，否则将qnew加入到随机树中。重复上述步骤直到qnearest和目标点qgaol距离小于一个阈值，则代表随机树到达了目标点，算法返回成功（6~7行）。为了使算法可控，可以设定运行时间上限或搜索次数上限（3行）。如果在限制次数内无法到达目标点，则算法返回失败。

为了加快随机树到达目标点的速度，简单的改进方法是：在随机树每次的生长过程中，根据随机概率来决定qrand是目标点还是随机点。在Sample函数中设定参数Prob （probability），每次得到一个0到1.0的随机值p，当0<p<Prob的时候，随机树朝目标点生长；当Prob<p<1.0时，随机树朝一个随机方向生长。

原文链接：https://blog.csdn.net/a735148617/article/details/103644670

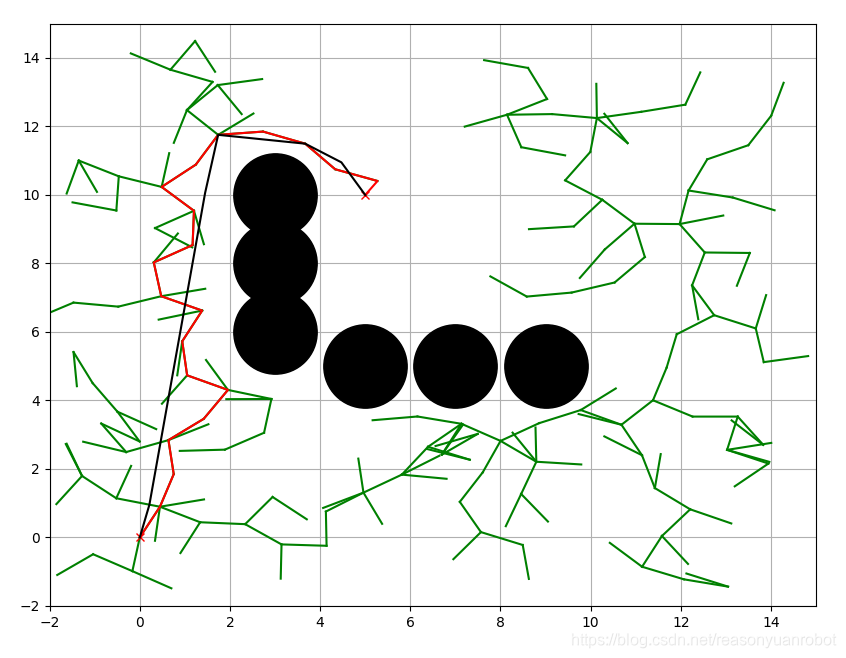
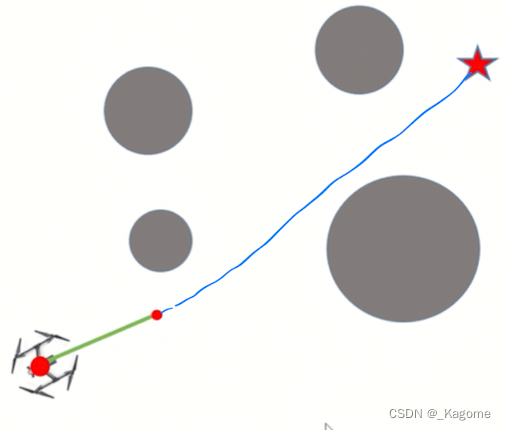
上图说明了RRT在有障碍物和没有障碍物的情况下探索自由空间的能力。这种特性通常被称为RRT的Voronoi偏差。作为均匀采样的结果，规划器更有可能在更大的Voronoi区域中选择样本，并且树朝着那个自由空间递增地快速增长。

RRT路径规划算法

https://blog.csdn.net/aoyousihaiqiuqihuang/article/details/100147478 matlab实现，包括后处理smooth

- 关于后处理，有不同的策略，文中采用的贪心策略，是相对简单的一种

一种后处理smooth策略：

#!/usr/bin/python
# -*- coding: UTF-8 -*-
import numpy as np
import random
import mathclass Smoother(object):"""@desc; 在规划好的path中，随机选择两个point(中间至少间隔一个point)，对选中的两个point采用固定长度的线性插值，若中间插值点未发生碰撞，则用该path替换之前两点之间的path"""def __init__(self):passdef __linecdchecker(self, start, goal):""":param start::param goal::return:"""nps = np.array(start).reshape(-1,1)npg = np.array(goal).reshape(-1,1)nele = math.ceil((abs(npg-nps)/self.__expanddis).max())ratio = np.linspace(0, 1, nele, endpoint=False)jointslist = (nps+(npg-nps)*ratio).T.tolist()for joints in jointslist:iscollided = self.__iscollidedcallback(joints, self.__obstaclelist, self.__robot, self.__cdchecker)if iscollided:return False, []return True, jointslistdef pathsmoothing(self, path, planner, maxiter):"""the path and planner are necessary parametersthe following member variables of planner will be used for smoothing1. jointlimits2. iscollidedcallback3. cdchecker4. robot5. expanddis6. obstaclelist:param path::param planner::return:"""self.__jointlimits = planner.jointlimitsself.__iscollidedcallback = planner.iscollidedcallbackself.__cdchecker = planner.cdcheckerself.__robot = planner.robotself.__expanddis = planner.expanddisself.__obstaclelist = planner.obstaclelistpathlength = len(path)if pathlength <= 3:return pathfor i in range(maxiter):pickpoint0 = random.randint(0, pathlength-3)pickpoint1 = random.randint(pickpoint0+1, pathlength-1)result, addpath = self.__linecdchecker(path[pickpoint0], path[pickpoint1])if result:path = path[:pickpoint0]+addpath+path[pickpoint1:]pathlength = len(path)return path

smooth效果：