论文链接:http://xxx.itp.ac.cn/pdf/2106.13008.pdf
Abstract
延长预测时间是极端天气预警和长期能源消耗规划等实际应用的关键需求。本文研究时间序列的长期预测问题。先前的基于 Transformer 的模型采用各种 self-attention 机制来发现长期依赖关系。然而,长期未来的复杂时间模式使基于 Transformer 的模型无法找到可靠的依赖关系。此外,Transformers 必须采用稀疏版本的 point-wise self-attentions 以获得长序列效率,从而导致信息利用瓶颈。除了 Transformers,我们将 Autoformer 设计为一种具有自相关机制的新型分解架构。我们打破了序列分解的预处理惯例,并将其更新为深度模型的基本内部块。这种设计为 Autoformer 赋予了复杂时间序列的渐进分解能力。此外,受随机过程理论的启发,我们设计了基于序列周期性的自相关机制,在子序列级别进行依赖关系发现和表示聚合。自相关在效率和准确性方面都优于self-attention。在长期预测中,Autoformer 产生了最先进的准确性,在六个基准上相对提高了 38%,涵盖了五个实际应用:能源、交通、经济、天气和疾病。此存储库中提供了代码:https://github.com/thuml/Autoformer。
总结
本文研究时间序列的长期预测问题,这是现实世界应用的迫切需求。 然而,复杂的时间模式阻止了模型学习可靠的依赖关系。 我们通过将序列分解模块嵌入为内部算子,提出 Autoformer 作为分解架构,它可以逐步聚合来自中间预测的长期趋势部分。 此外,我们设计了一种高效的Auto-Correlation 机制来在序列级别进行依赖关系发现和信息聚合,这与之前的self-attention家族形成鲜明对比。 Autoformer 可以自然地实现 O(L log L) 复杂度,并在广泛的现实世界数据集中产生一致的最新性能。
1 Introduction
时间序列预测已广泛应用于能源消费、交通与经济规划、天气与疾病传播预测等方面。在这些实际应用中,一个迫切的需求是将预测时间延伸到遥远的未来,这对长期规划和预警非常有意义。因此,本文研究时间序列的长期预测问题,其特点是预测时间序列的长度较大。最近的深度预测模型[48,23,26,34,29,35,25,41]取得了很大的进展,特别是基于transformer的模型。得益于self-attention 机制,transformer在对序列数据的长期依赖进行建模方面获得了很大的优势,这使得更强大的大模型成为可能[8,13]。
然而,在长期设置下的预测任务是极具挑战性的。首先,直接从长期时间序列中发现时间依赖关系是不可靠的,因为这些依赖关系可能被混乱的时间模式所掩盖。其次,由于序列长度的平方复杂度,具有自我注意机制的典型 Transformers 在计算上无法用于长期预测。以往基于Transformers的预测模型[48,23,26]主要关注于将 self-attention提高到稀疏版本。虽然性能得到了显著提高,但这些模型仍然利用了point-wise 表示聚合。因此,在提高效率的过程中,由于 point-wise 连接稀疏,会牺牲信息的利用,从而造成时间序列长期预测的瓶颈。
为了对复杂的时间模式进行推理,我们尝试采用分解的思想,这是时间序列分析中的标准方法[1,33]。它可以用于处理复杂的时间序列和提取更可预测的组件。但是在预测的背景下,由于未来是未知的[20],只能作为过去序列的预处理。这种常见的用法限制了分解的能力,并忽略了分解组件之间潜在的未来交互。因此,我们试图超越分解的预处理使用,并提出一个通用的体系结构,使深度预测模型具有渐进分解的内在能力。进一步,分解可以解开纠缠的时间模式,突出时间序列[20]的固有属性。基于此,我们尝试利用序列的周期性来修复self-attention中的point-wise连接。我们观察到,在同一相位的各时期子序列往往表现出相似的时间过程。因此,我们试图基于由序列周期性导出的过程相似度构建一个 series-level 连接。
基于上述动机,我们提出一种原始的Autoformer来代替transformer进行长期时间序列预测。Autoformer仍然遵循残差和编码器-解码器结构,但将Transformer更新为分解预测架构。通过嵌入我们提出的分解块作为内部算子,Autoformer可以逐步从预测的隐藏变量中分离出长期趋势trend信息。这种设计允许我们的模型在预测过程中交替分解和细化中间结果。受随机过程理论的启发[9,30],Autoformer引入了一种自相关机制来代替self-attention,它基于序列的周期性发现子序列的相似性,并从潜在的周期中聚合相似子序列。这种按序列的机制实现了长度 L 序列的复杂度,并通过将 point-wise 表示聚合扩展到子序列级别,打破了信息利用瓶颈。Autoformer在6个基准上达到了最先进的精度。其贡献总结如下:
- 为了解决长期未来的复杂时间模式,我们提出Autoformer作为一个分解体系结构,并设计内部分解模块,使深度预测模型具有内在的渐进分解能力。
- 我们提出了一种基于序列级依赖项发现和信息聚合的自相关 Auto-Correlation 机制。该机制超越了以往的self-attention family,同时提高了计算效率和信息利用率。
- Autoformer在六个基准的长期设置下实现了38%的相对改善,涵盖了五个真实世界的应用:能源、交通、经济、天气和疾病。
2 Related Work
2.1 Models for Time Series Forecasting
由于时间序列预测的巨大重要性,各种模型已经得到很好的发展。许多时间序列预测方法都是从经典工具开始的[38,10]。ARIMA[7,6]通过差分将非平稳过程转化为平稳过程来解决预测问题。在序列预测中也引入了滤波方法[24,12]。此外,利用循环神经网络(RNNs)模型对时间序列的时间相关性进行建模[42,32,47,28]。DeepAR[34]结合了自回归方法和RNNs来建模未来序列的概率分布。LSTNet[25]引入了带有 recurrent-skip connections 的卷积神经网络(CNNs),以捕获短期和长期的时间模式。基于注意的RNNs[46,36,37]引入了时间注意来探索长期相关性,以进行预测。此外,许多基于时间卷积网络(TCN)的研究[40,5,4,35]试图用因果卷积来建模时间因果关系。这些深度预测模型主要是通过recurrent connections、temporal attention或因果卷积causal convolution建立时间关系模型。
近年来,基于 self-attention 的 Transformers [41,45]在序列数据处理方面表现出了强大的能力,如自然语言处理[13,8]、音频处理[19],甚至计算机视觉[16,27]。然而,由于序列长度 L 在记忆和时间上的平方复杂度,将 self-attention 应用于长期时间序列预测在计算上是不允许的。LogTrans[26]将局部卷积引入到Transformer中,并提出 LogSparse attention来选择指数增长间隔之后的时间步长,将复杂度降低到。Reformer [23]提供了local-sensitive hashing (LSH) attention,并将复杂性降低到
。Informer [48]使用基于KL-divergence的ProbSparse attention扩展了Transformer,并且实现了
复杂度。请注意,这些方法基于普通的Transformer,并尝试将 self-attention 机制改进为稀疏版本,该版本仍然遵循 point-wise 依赖和聚合。本文提出的 Auto-Correlation 机制基于时间序列的固有周期性,能够提供 series-wise 连接。
2.2 时间序列的分解
作为时间序列分析中的一种标准方法,时间序列分解 [1, 33] 将时间序列解构为几个部分,每个部分代表一种更可预测的基本模式类别。它主要用于探索随着时间推移的历史变化。对于预测任务,在预测未来序列 [20, 2] 之前,总是使用分解作为历史序列的预处理,例如带有 trend-seasonality 分解的 Prophet [39] 和带有基扩展(basis expansion)的N-BEATS [29] 和 使用矩阵分解的DeepGLO[35] 。然而,这种预处理受限于历史序列的简单分解效应,并忽略了长期未来序列底层模式之间的层次交互。本文从一个新的渐进维度提出分解思想。我们的 Autoformer 将分解作为深度模型的内部块,它可以在整个预测过程中逐步分解隐藏序列,包括过去的序列和预测的中间结果。
3 Autoformer
时间序列预测问题是在给定过去的 length-I 序列的情况下预测未来最可能的 length-O 序列,表示为 input-I-predict-O 。long-term forecasting 设置是预测长期的未来,即 larger O。如前所述,我们强调了长期序列预测的困难:处理复杂的时间模式,打破计算效率和信息利用的瓶颈。 为了解决这两个挑战,我们将分解作为内置模块引入深度预测模型,并提出 Autoformer 作为分解架构。 此外,我们设计了自相关(Auto-Correlation)机制来发现基于周期的依赖关系并聚合来自底层周期的相似子系列。
3.1 分解架构
我们将 Transformer [41] 更新为深度分解架构(图 1),包括内置序列分解模块、Auto-Correlation机制以及相应的Encoder and Decoder。
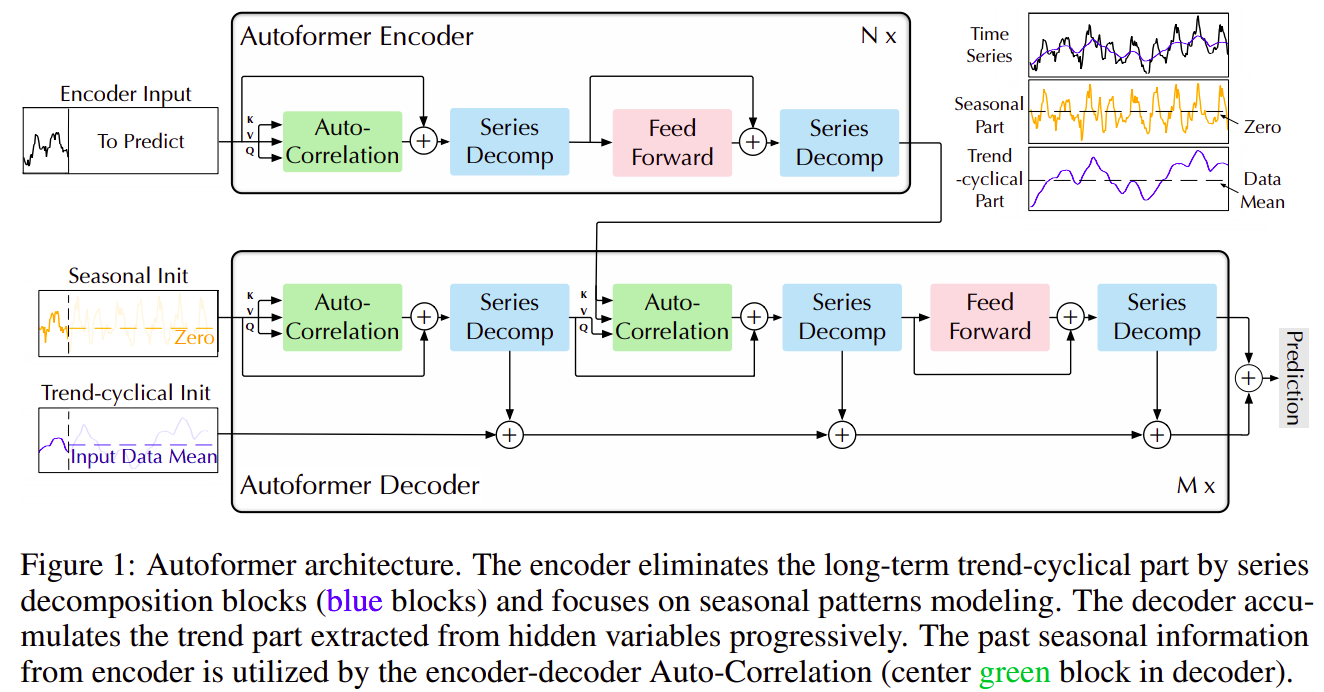
图1:Autoformer 架构。Encoder 通过序列分解模块(蓝色模块)消除了 long-term trend-cyclical 部分,并专注于 seasonal 模式建模。 Decoder 逐步累积从隐藏变量中提取的 trend 部分。 encoder-decoder Auto-Correlation(Decoder 中的中间绿色块)利用来自 encoder 的过去 seasonal 信息。
序列分解模块
为了在 long-term 预测上下文中学习复杂的时间模式,我们采用分解的思想 [1, 33],它可以将序列分为trend-cyclical 部分和 seasonal 部分。 这两个部分分别反映了该序列的 long-term 发展和seasonality。 然而,对于未来的序列来说,直接分解是无法实现的,因为未来是未知的。 为了解决这个难题,我们提出了一个序列分解模块作为 Autoformer 的内部操作(图 1),它可以从预测的中间隐藏变量中逐步提取 long-term 平稳 trend 。 具体而言,我们采用 moving average 以平滑周期性波动并突出long-term trends。 对于 length-L 的输入序列 ,过程为:
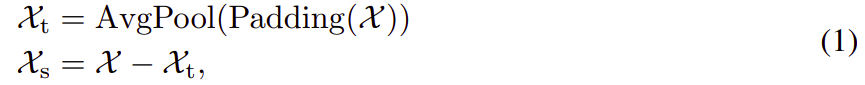
这里 分别代表 seasonal 部分和 提取的 trend-cyclical 部分。我们采用 带有 padding 操作的AvgPool(·) 进行 moving average ,填充操作用来保持序列长度不变。我们用
来总结上面的方程,这是一个模型内部模块。
模型输入
Encoder 部分的输入是过去的 I 个时间步 。作为一种分解架构(图 1),Autoformer decoder 的输入包含要细化的 seasonal 部分
和 trend-cyclical 部分
。 每个初始化由两部分组成:由 encoder 的输入
的后半部分分解而成,用 length
以提供最近的信息,长度为 O 的占位符由标量填充。 其公式如下:
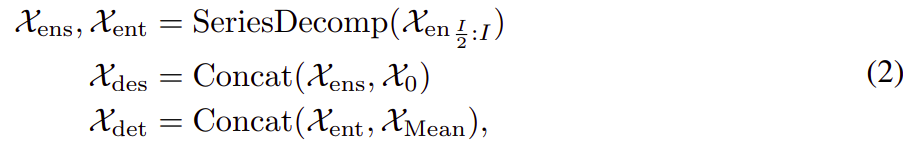
这里 分别表示
的 seasonal 部分和 trend-cyclical 部分;
分别表示被0 填充的占位符和被
的mean填充的占位符。
Encoder
如图 1 所示,encoder 侧重于 seasonal 部分建模。 encoder 的输出包含过去的 seasonal 信息,将作为交叉(cross)信息帮助 decoder 细化预测结果。 假设我们有 N 个 encoder 层。第个encoder 的整体方程总结为
。 详情如下:

这里 “_” 是消除的trend部分;![]() 表示第
表示第个encoder层的输出;
表示
的嵌入,
![]() 表示在第
表示在第层中的第
个序列分解模块后的 seasonal 部分。我们将在下一节中详细描述 Auto-Correlation(·),它可以无缝地替代 self-attention。
Decoder
Decoder 包含两部分:trend-cyclical 部分的累积结构和seasonal 部分的堆叠 Auto-Correlation机制(图 1)。 每个 Decoder 层包含 inner Auto-Correlation 和 encoder-decoder Auto-Correlation,它们可以分别细化预测和利用过去的 seasonal 信息。 请注意,该模型在 Decoder 期间从中间隐藏变量中提取潜在 trend,从而允许 Autoformer 逐步细化trend预测并消除干扰信息,以便在Auto-Correlation 中发现基于周期的依赖关系。 假设有 M 个 decoder 层。 使用来自 encoder 的隐变量 ,第
个解码器层的方程可以概括为
。Decoder 可以如下公式化:
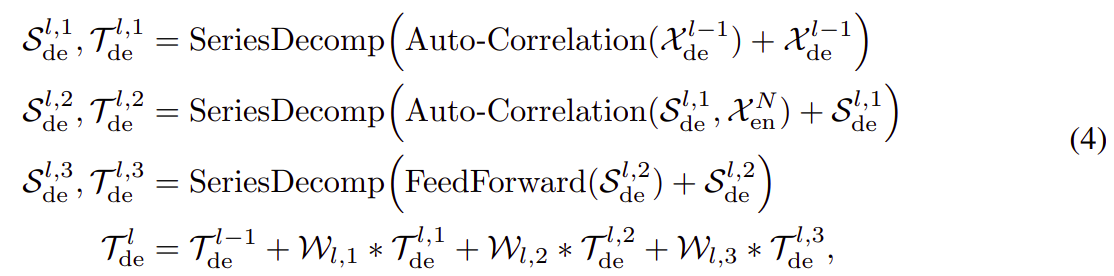 这里,
这里,![]() 表示第
表示第 个解码器层的输出;
是
的 嵌入,用于深度变换,
![]() 用于累积。
用于累积。![]() 分别表示 在第
分别表示 在第层中的第
个序列分解模块后seasonal 分量和 trend-cyclical 分量。
![]() 表示第
表示第 个提取的 trend
的投影。
最终的预测是两个细化的分解分量之和,为 ![]() ,其中
,其中 是用来将深度变换的seasonal 分量
投影到目标维度。
3.2 Auto-Correlation 机制
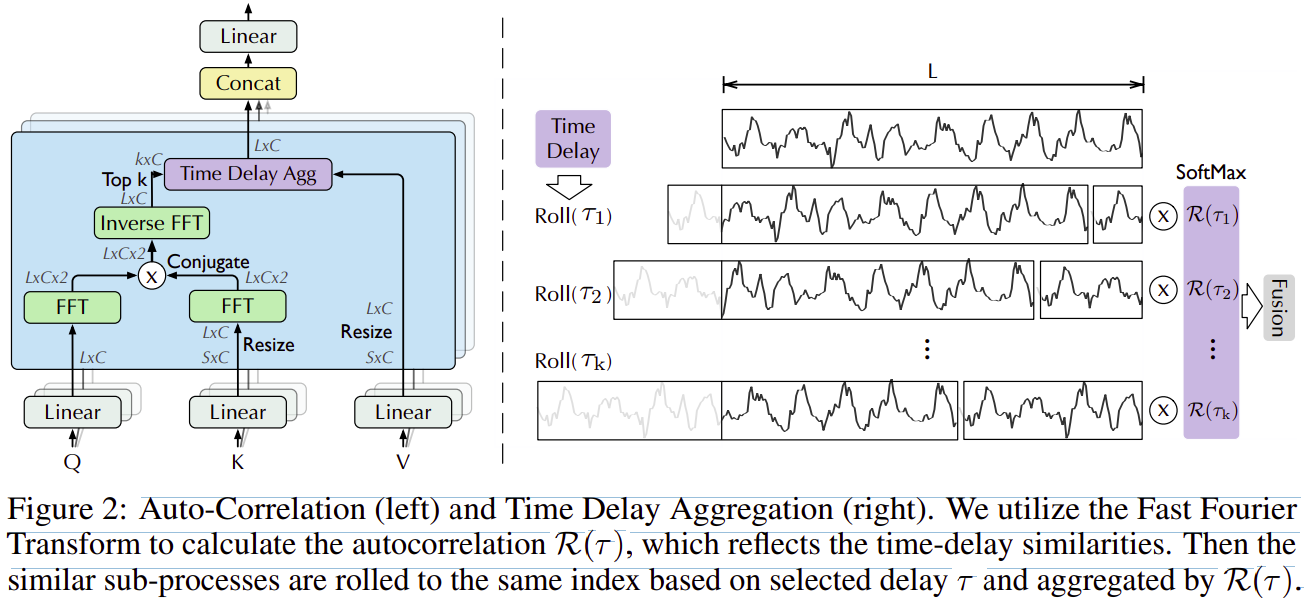
图2:Auto-Correlation(左)和时间延迟聚合 Time Delay Aggregation(右)。 我们利用快速傅里叶变换来计算自相关 ![]() ,它反映了时延相似性。 然后基于选定的延迟
,它反映了时延相似性。 然后基于选定的延迟 将相似的子过程滚动到相同的索引,并通过
![]() 聚合。
聚合。
如图2所示,我们提出了具有 series-wise(序列级) 连接的自相关机制来扩展信息利用率。 自相关通过计算序列自相关来发现基于周期的依赖关系,并通过时间延迟聚合来聚合相似的子序列。
Period-based dependencies 基于周期的依赖
可以观察到,周期之间相同的相位自然会提供相似的子过程。受随机过程理论 [9, 30] 的启发,对于一个真正的离散时间过程 {},我们可以通过以下等式获得autocorrelation
![]() :
:
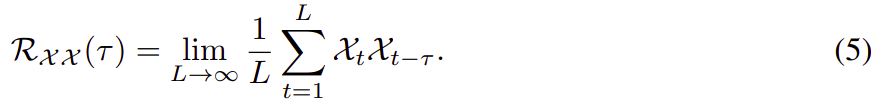
![]() 反映了 {
反映了 {} 与其
延迟序列 {
} 之间的时延相似性。 如图 2 所示,我们使用autocorrelation
![]() 作为估计周期长度
作为估计周期长度 的非归一化置信度。 然后,我们选择最可能的k个周期长度
,···,
。 基于周期的依赖关系是由上述估计的周期得出的,并且可以通过相应的自相关来加权。
Time delay aggregation
基于周期的依赖关系连接估计周期之间的子序列。 因此,我们提出了时间延迟聚合模块(图 2),它可以根据选定的时间延迟 ,···,
滚动序列。 该操作可以对齐在估计周期的相同相位位置的相似子序列,这与self-attention 系列中的 point-wise dot-product aggregation不同。 最后,我们通过 softmax 归一化置信度聚合子序列。
对于single head 情况和 length-L 的时间序列X,经过投影,我们得到query Q、key K和value V。这样就可以无缝替换self-attention。 自相关机制是:
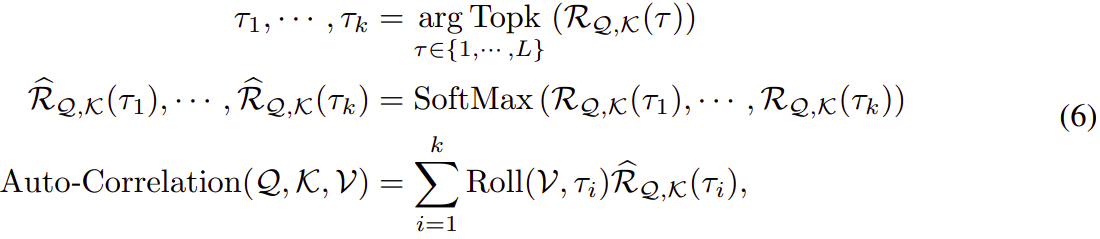 其中 arg Topk(·) 是为了得到 Topk 自相关的参数,并且 让
其中 arg Topk(·) 是为了得到 Topk 自相关的参数,并且 让 ![]() ,c 是一个超参数。
,c 是一个超参数。 ![]() 是序列 Q 和 K 之间的自相关。
是序列 Q 和 K 之间的自相关。![]() 表示以时间延迟
表示以时间延迟 对 X 进行操作,在此期间,将超出第一个位置的元素重新引入最后一个位置。 对于encoder-decoder Auto-Correlation(图 1),K、V 是来encoder的
并将被调整为length-O,Q 来自于decoder的前一个模块。
对于 Autoformer 中使用的 multi-head 版本,带有 通道的隐变量,h heads,第
个head的query, key, value是
![]() 。 过程是:
。 过程是:
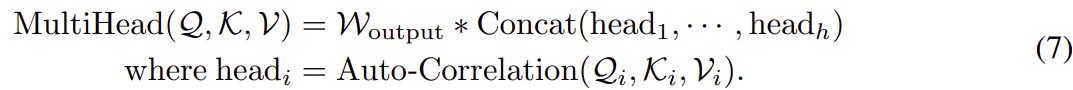
Efficient computation
对于基于周期的依赖,这些依赖指向与底层周期相同相位的子过程,并且本质上是稀疏的。 在这里,我们选择最可能的延迟以避免选择相反的相位。 因为我们聚合了长度为 L 的 O(log L) 序列,所以方程 6 和方程 7 的复杂度为 O(L log L)。 对于自相关计算(方程 5),给定时间序列 {},
![]() 可以通过基于 Wiener-Khinchin 定理 [43] 的 快速傅里叶变换 (FFT) 计算:
可以通过基于 Wiener-Khinchin 定理 [43] 的 快速傅里叶变换 (FFT) 计算:
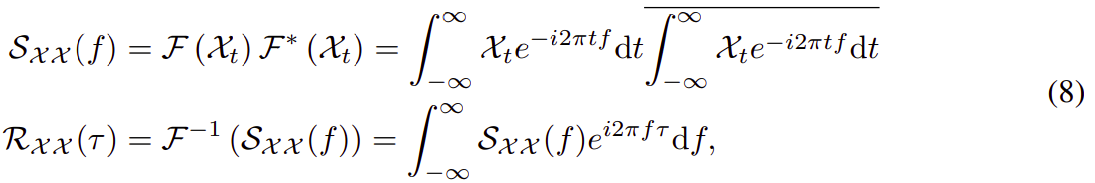
其中 ![]() ,
, 表示 FFT,
是它的逆变换。 ∗ 表示共轭运算,
![]() 在频域中。 请注意,{1,····,L} 中所有延迟的序列自相关可以通过 FFT 一次计算。 因此,自相关实现了 O(L log L) 复杂度。
在频域中。 请注意,{1,····,L} 中所有延迟的序列自相关可以通过 FFT 一次计算。 因此,自相关实现了 O(L log L) 复杂度。
Auto-Correlation vs. self-attention family
与point-wise self-attention family不同,自相关呈现 series-wise 连接(图 3)。 具体来说,对于时间依赖关系,我们根据周期性找到子序列之间的依赖关系。 相比之下,self-attention family 只计算散点之间的关系。 尽管一些 self attention [26, 48] 考虑了 local 信息,但它们仅利用此信息来帮助发现点依赖关系。 对于信息聚合,我们采用时间延迟模块来聚合来自底层时期的相似子序列。 相反,self-attentions 通过点积聚合选择的点。 得益于固有的稀疏性和 sub-series-level 表示聚合,自相关可以同时提高计算效率和信息利用率。
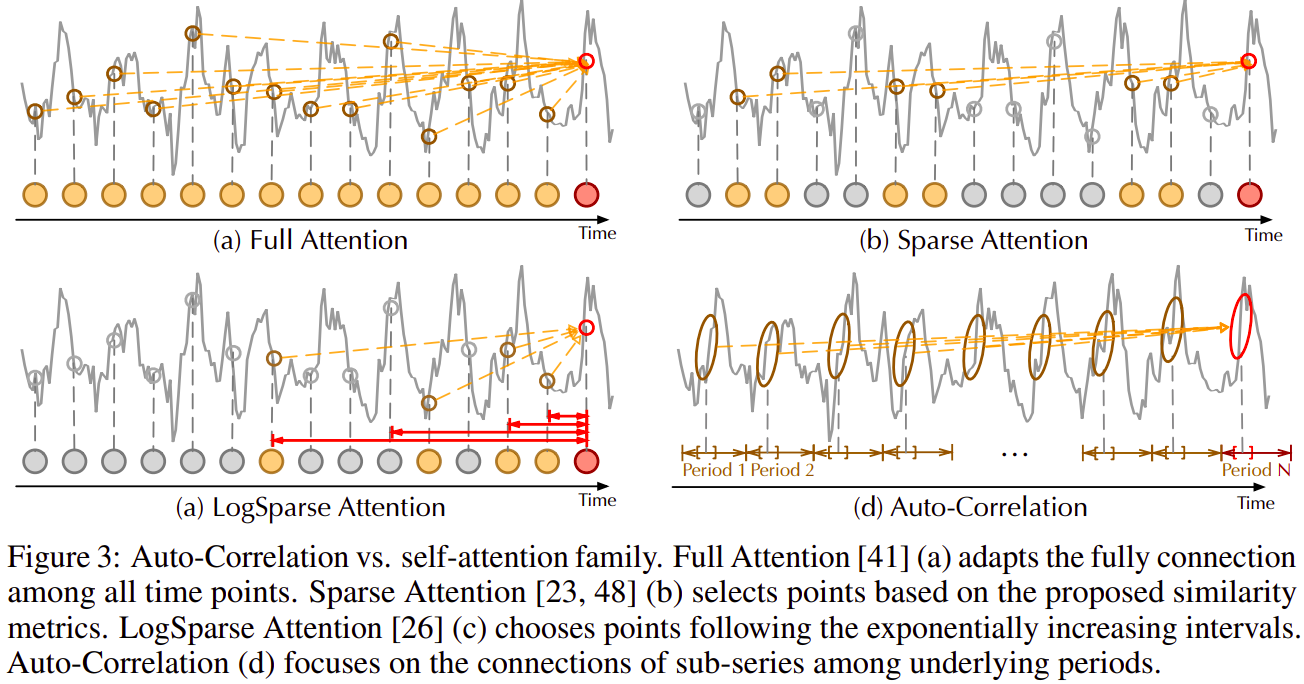
图 3:Auto-Correlation vs. self-attention family。Full Attention [41] (a) 适应所有时间点之间的完全连接。 Sparse Attention [23, 48] (b) 根据提出的相似度指标选择点。 LogSparse Attention [26] (c) 选择遵循指数增长区间的点。 自相关 (d) 侧重于子系列在底层周期之间的联系。

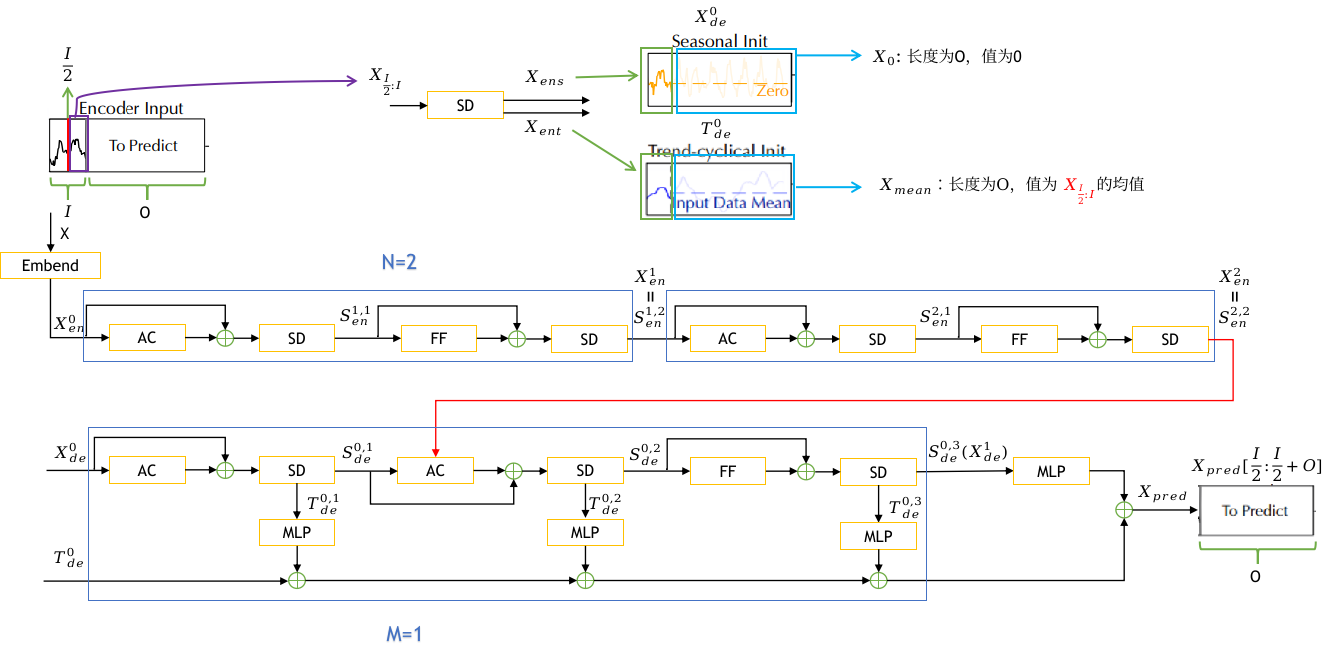
编码器部分只传递 seasonal 分量,舍弃 trend-cyclical 分量。
参考:
可以看下原作的问题回复
细读好文 之 Autoformer: Decomposition Transformers with Auto-Correlation for Long-Term Series Forecasting - 知乎
Autoformer:基于深度分解架构和自相关机制的长期序列预测模型 - 知乎
有个讲解视频:
[论文精读] Autoformer:基于深度分解架构和自相关机制的长期序列预测模型_哔哩哔哩_bilibili