http://blog.csdn.net/pipisorry/article/details/62053938

时间序列简介

时间序列是时间间隔不变的情况下收集的时间点集合。这些集合被分析用来了解长期发展趋势，为了预测未来或者表现分析的其他形式。但是什么时间序列？与常见的回归问题的不同？

1、时间序列是跟时间有关的。所以基于线性回归模型的假设：观察结果是独立的。在这种情况下是不成立的。

2、随着上升或者下降的趋势，更多的时间序列出现季节性趋势的形式，如：特定时间框架的具体变化。即：如果你看到羊毛夹克的销售上升，你就一定会在冬季做更多销售。

因为时间序列的固有特性，有各种不同的步骤可以对它进行分析。

时间序列的数据格式[pandas时间序列分析和处理Timeseries ]

Note: pandas时间序列series的index必须是DatetimeIndex不能是Index，也就是如果index是从dataframe列中转换来的，其类型必须是datetime类型，不能是date、object等等其它类型！否则会报错：AttributeError: 'Index' object has no attribute 'inferred_freq'。[Decomposing trend, seasonal and residual time series elements]

什么导致时间序列不稳定？

这儿有两个主要原因。

趋势-随着时间产生不同的平均值。举例：在飞机乘客这个案例中，我们看到总体上，飞机乘客的数量是在不断增长的。
季节性-特定时间框架内的变化。举例：在特定的月份购买汽车的人数会有增加的趋势，因为车价上涨或者节假日到来。

模型的根本原理或者预测序列的趋势和季节性，从序列中删除这些因素，将得到一个稳定的序列。然后统计预测技术可以在这个序列上完成。最后一步是通过运用趋势和季节性限制倒回到将预测值转换成原来的区间。

时间序列的稳定性

如果一个时间序列的统计特征如平均数，方差随着时间保持不变，我们就可以认为它是稳定的。稳定性的确定标准是非常严格的。但是，如果时间序列随着时间产生恒定的统计特征，根据实际目的我们可以假设该序列是稳定的。如下：

恒定的平均数
恒定的方差
不随时间变化的自协方差

为什么时间序列的稳定性这么重要？

大部分时间序列模型是在假设它是稳定的前提下建立的。直观地说，我们可以这样认为，如果一个时间序列随着时间产生特定的行为，就有很高的可能性认为它在未来的行为是一样的。同时，根据稳定序列得出的理论是更加成熟的，也是更容易实现与非稳定序列的比较。

时间序列的稳定性测试

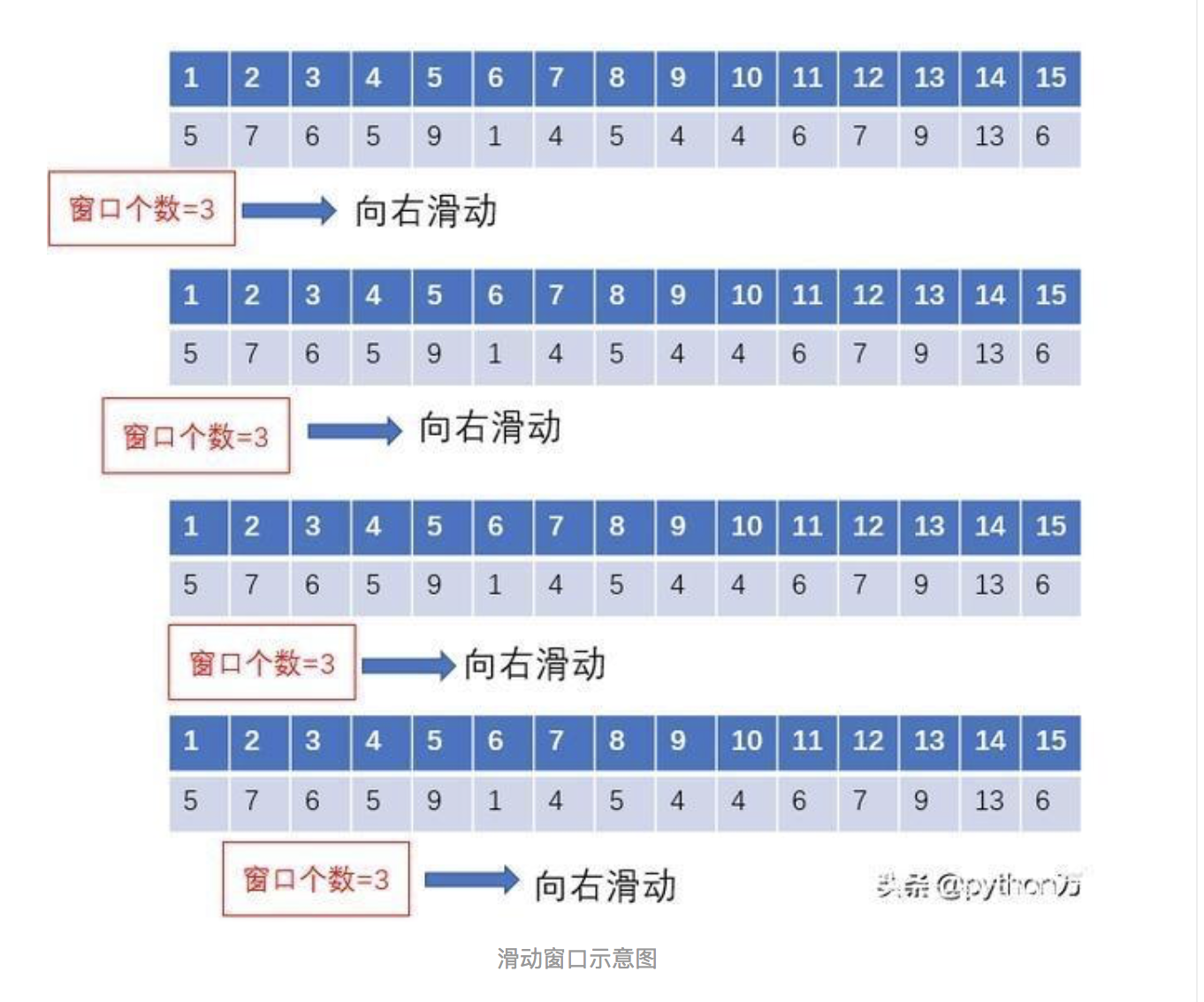
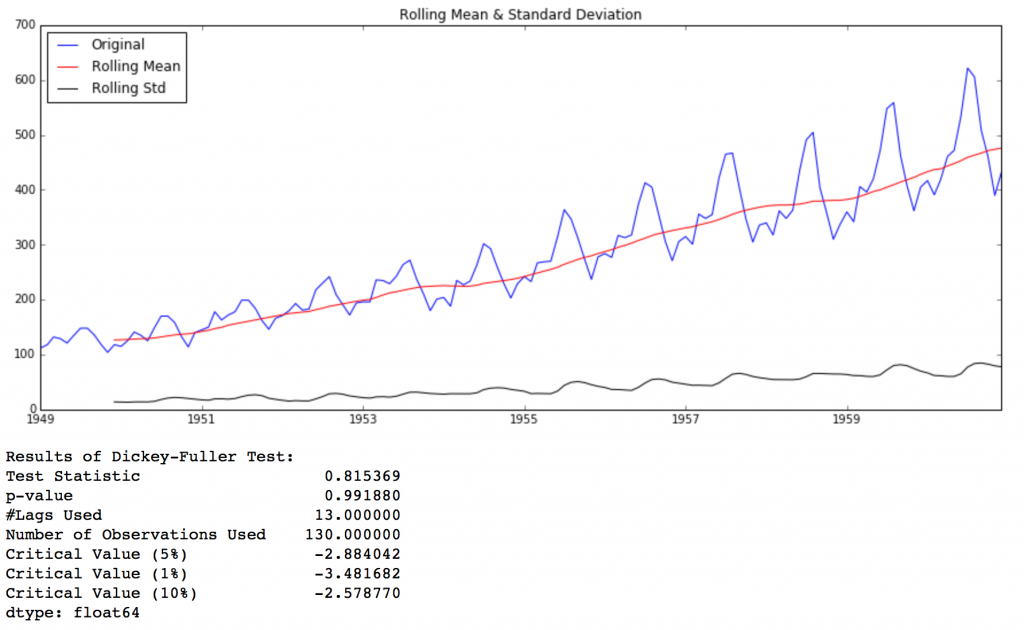
1、绘制滚动统计：我们可以绘制移动平均数和移动方差，观察它是否随着时间变化。随着移动平均数和方差的变化，我认为在任何“t”瞬间，我们都可以获得去年的移动平均数和方差。如：上一个12个月份。但是，这更多的是一种视觉技术。

2、DF检验：这是一种检查数据稳定性的统计测试。无效假设：时间序列是不稳定的。测试结果由测试统计量和一些置信区间的临界值组成。如果“测试统计量”少于“临界值”，我们可以拒绝无效假设，并认为序列是稳定的。[假设检验-t检验和Augmented Dickey–Fuller test ]

from statsmodels.tsa.stattools import adfuller
def test_stationarity(timeseries):#Determing rolling statisticsrolmean = pd.rolling_mean(timeseries, window=12)rolstd = pd.rolling_std(timeseries, window=12)#Plot rolling statistics:orig = plt.plot(timeseries, color='blue',label='Original')mean = plt.plot(rolmean, color='red', label='Rolling Mean')std = plt.plot(rolstd, color='black', label = 'Rolling Std')plt.legend(loc='best')plt.title('Rolling Mean & Standard Deviation')plt.show(block=False)#Perform Dickey-Fuller test:print 'Results of Dickey-Fuller Test:'dftest = adfuller(timeseries, autolag='AIC')dfoutput = pd.Series(dftest[0:4], index=['Test Statistic','p-value','#Lags Used','Number of Observations Used'])for key,value in dftest[4].items():dfoutput['Critical Value (%s)'%key] = valueprint dfoutput

The code is pretty straight forward. Please feel free to discuss the code in comments if you face challenges in grasping it.

Let’s run it for our input series:

test_stationarity(ts)

皮皮blog

趋势减少技术

消除趋势的第一个方法是转换。例如,在本例中,我们可以清楚地看到,有一个显著的趋势。所以我们可以通过变换，惩罚较高值而不是较小值。这可以采用log,平方根,立方跟等等。

ts_log = np.log(ts)

我们可以使用一些技术来估计或对这个趋势建模,然后将它从序列中删除：

聚合Aggregation – taking average for a time period like monthly/weekly averages取一段时间的平均值（月/周平均值）

平滑Smoothing – taking rolling averages取滚动平均数

多项式回归分析Polynomial Fitting – fit a regression model适合的回归模型

平滑

移动平均

（英语：Moving Average，MA），又称“移动平均线”（简称均线），也称为滚动平均数（Rolling Average）、滚动平均值或运行平均值，是技术分析中一种分析时间序列数据的工具。移动平均可抚平短期波动，反映出长期趋势或周期。数学上，移动平均可视为一种卷积。

最常见的是利用股价、回报或交易量等变数计算出移动平均。

简单移动平均（英语：Simple Moving Average，SMA）是某变数之前n个数值的未作加权算术平均。例如，收市价的10日简单移动平均指之前10日收市价的平均数。

加权移动平均（英语：Weighted Moving Average，WMA）指计算平均值时将个别数据乘以不同数值，在技术分析中，n日WMA的最近期一个数值乘以n、次近的乘以n-1，如此类推，一直到0。

指数移动平均（英语：Exponential Moving Average，EMA或EWMA）是以指数式递减加权的移动平均。各数值的加权影响力随时间而指数式递减，越近期的数据加权影响力越重，但较旧的数据也给予一定的加权值。加权的程度以常数α决定，α数值介乎0至1。

一般形式

{\text{EMA}}={p_{1}+(1-\alpha )p_{2}+(1-\alpha )^{2}p_{3}+(1-\alpha )^{3}p_{4}+\cdots \over 1+(1-\alpha )+(1-\alpha )^{2}+(1-\alpha )^{3}+\cdots }

α可能的取值方法有

com :     Specify decay in terms of center of mass, \alpha = 1 / (1 + com), for com >= 0
span :    Specify decay in terms of span, \alpha = 2 / (span + 1), for span > 1
halflife : 使用参数“半衰期”来定义指数衰减量Specify decay in terms of half-life, \alpha = 1 - exp(log(0.5) / halflife), for halflife > 0   lz感觉0.5应该改成2？？或者pandas内部有相应的转换？

span: α用天数N来代表： $\alpha ={2 \over {N+1}}$ ，所以，N=19天，代表α=0.1

halflife : 在使用halflife计算移动平均时候，EMA计算中(1-α)的指数项为负数，表示与当前时间t的差值？如计算2017.2.30的EMA时，2017.2.29的指数项为-1。而在2017.2.15时，如果halflife设置为15，则p_{2015.2.15}的权重为(1-α)^-15 = (exp(log(0.5) / 15)^-15 = (exp(log(0.5) / 15 ^-15) = exp(-log0.5) = 2?

[wikipedia移动平均]

指数衰减

某个量的下降速度和它的值成比例，称之为服从指数衰减。用符号可以表达为以下微分方程，其中N是指量，λ指衰减常数（或称衰变常数）。 ${\ {dN}{dt}}=-\lambda N.$

方程的一个解为： $N(t)=N_{0}e^{-\lambda t}.\,$

平均寿命

如果这个衰减量是一个集合中的离散元素，可以计算元素留在集合中的平均时间长度。这被称为平均寿命（一般称寿命）。并且它可以被证明与衰减速率有关。 $\tau ={\frac {1}{\lambda }}.$

平均时间（或被称为指数时间常数）由此被看做一个简单的缩放时间：

N(t)=N_{0}e^{-t/\tau }.\,

因而，这是量减少到初始量的1/e所需要的时间。

类似的，下面所述的以2为底的指数缩放时间为半衰期

半衰期

对多数人而言更加直观的一个典型指数衰减是当量减少为初始量的一半所需要的时间。这个时间被称为半衰期，表示为 t 0.5 {\displaystyle t_{0.5}} $t_{0.5}$ 。

半衰期可以被写作衰减常数或者平均寿命的形式： $t_{0.5}={\frac {\ln 2}{\lambda }}=\tau \ln 2.$

代入 $\tau$ $N(t)=N_{0}2^{-t/t_{0.5}}.\,$

平均寿命 τ {\displaystyle \tau } $\tau$ 等于半衰期除以ln2，或： $\tau ={\frac {t_{0.5}}{ln2}}\approx 1.442695040888963t_{0.5}.$

[wikipedia指数衰减]

皮皮blog

pandas实现

简单移动平均rolling

这个方法有一个缺陷：要严格定义时段。在这种情况下，我们可以采用年平均数，但是对于复杂的情况的像预测股票价格，是很难得到一个数字的。所以，我们采取“加权移动平均法”可以对最近的值赋予更高的权重。

Note: 前面window个rolling值是Nan，我们要丢掉这些NaN值。

Series.rolling(window, min_periods=None, freq=None, center=False, win_type=None, on=None, axis=0)

主要参数

window : int, or offset
Size of the moving window. This is the number of observations used for calculating the statistic. Each window will be a fixed size.
If its an offset then this will be the time period of each window. Each window will be a variable sized based on the observations included in the time-period. This is only

valid for datetimelike indexes.

min_periods : int, default None
Minimum number of observations in window required to have a value (otherwise result is NA). For a window that is specified by an offset, this will default to 1.

center : boolean, default False
Set the labels at the center of the window. By default, the result is set to the right edge of the window. This can be changed to the center of the window by setting center=True.也就是rolling方法默认是将如2011.2.1 ～ 2011.2.30的均值设置为2011.2.30的均值，center=True则是将2011.2.1 ～ 2011.2.30的均值设置为2011.2.15对应的均值。相当于将rolling线向前移动了window/2个单位。

win_type : string, default None lz猜测应该是取变长window的意思，没用过。这样的话时间间隔长的timeseries的window可能小点。

Provide a window type. See the notes below.

on : string, optional
For a DataFrame, column on which to calculate the rolling window, rather than the index.

[ref & Examples pandas.Series.rolling]

指数移动平均ewm

Note: （不同于rolling）在这种情况下就不会有遗漏值因为所有的值在一开始就被赋予了权重。所以在运行的时候，它没有先前的值参与。

Series.ewm(com=None, span=None, halflife=None, alpha=None, min_periods=0, freq=None, adjust=True, ignore_na=False, axis=0)

主要参数

com : float, optional
    Specify decay in terms of center of mass, \alpha = 1 / (1 + com), for com >= 0
span : float, optional
    Specify decay in terms of span, \alpha = 2 / (span + 1), for span > 1
halflife : float, optional
    Specify decay in terms of half-life, \alpha = 1 - exp(log(0.5) / halflife), for halflife > 0

alpha : float, optional
Specify smoothing factor \alpha directly, 0 < \alpha <= 1

[pandas.Series.ewm]

皮皮blog

趋势和季节性消除技术

差分Differencing – taking the differece with a particular time lag采用一个特定时间差的差值

分解Decomposition – modeling both trend and seasonality and removing them from the model.建立有关趋势和季节性的模型和从模型中删除它们

差分Differencing

处理趋势和季节性的最常见的方法之一就是差分法。在这种方法中,我们采用特定瞬间和它前一个瞬间的不同的观察结果。这主要是在提高平稳性。

一般可以很大程度上减少了趋势。同样可以采取二阶或三阶差分在具体应用中获得更好的结果。

前向差分

前向差分有时候也称作数列的二项式变换

函数的前向差分通常简称为函数的差分。对于函数 f ( x ) {\displaystyle \ f(x)} $\ f(x)$ ，如果在等距节点：

x_{k}=x_{0}+kh,(k=0,1,...,n)

\ \Delta f(x_{k})=f(x_{​{k+1}})-f(x_{k})

则称 Δ f ( x ) {\displaystyle \ \Delta f(x)} $\ \Delta f(x)$ ，函数在每个小区间上的增量 y k + 1 − y k {\displaystyle y_{k+1}-y_{k}} $y_{{k+1}}-y_{k}$ 为 f ( x ) {\displaystyle \ f(x)} $\ f(x)$ 一阶差分。

在微积分学中的有限差分（finite differences），前向差分通常是微分在离散的函数中的等效运算。差分方程的解法也与微分方程的解法相似。当 f ( x ) {\displaystyle \ f(x)} $\ f(x)$ 是多项式时，前向差分为Delta算子（称 Δ {\displaystyle \Delta } $\Delta$ 为差分算子[2]），一种线性算子。前向差分会将多项式阶数降低 1。

逆向差分

对于函数 f ( x k ) {\displaystyle \ f(x_{k})} $\ f(x_{k})$ ，如果： $\ \nabla f(x_{k})=f(x_{k})-f(x_{{k-1}}).\,$ 则称 ∇ f ( x k ) {\displaystyle \ \nabla f(x_{k})} $\ \nabla f(x_{k})$ 为 f ( x ) {\displaystyle \ f(x)} $\ f(x)$ 的一阶逆向差分。

差分的阶

一阶差分的差分为二阶差分，二阶差分的差分为三阶差分，其余类推。记： $\ \Delta ^{n}[f](x)$ 为 f ( x ) {\displaystyle \ f(x)} $\ f(x)$ 的 n {\displaystyle \ n} $\ n$ 阶差分。

如果

\ \Delta ^{n}[f](x)

\ =\Delta \{\Delta ^{​{n-1}}[f](x)\}

\ =\Delta ^{​{n-1}}[f](x+1)-\Delta ^{​{n-1}}[f](x)

根据数学归纳法，有

\ \Delta ^{n}[f](x)=\sum _{​{i=0}}^{n}{n \choose i}(-1)^{​{n-i}}f(x+i)

其中，

\ {n \choose i}

为二项式系数。

特别的，有 $\ \Delta ^{2}[f](x)=f(x+2)-2f(x+1)+f(x)$

[wikipedia差分]

与差分相关的均差参考[数据插值方法]

Pandas实现

Series.shift(periods=1, freq=None, axis=0)[pandas.Series.shift]

shift示例

se
se.shift()

2013-01-01    0
2013-01-02    1
2013-01-03    2
2013-01-04    5
2013-01-05    4

2013-01-01    NaN
2013-01-02    0.0
2013-01-03    1.0
2013-01-04    2.0
2013-01-05    5.0

pandas实现一阶差(前向差分)示例

ts_diff = ts - ts.shift()

分解：趋势+季节性+残差

在这种方法中,趋势和季节性是分别建模的并倒回到序列的保留部分。

from statsmodels.tsa.seasonal import seasonal_decompose
decomposition = seasonal_decompose(ts_log)trend = decomposition.trend
seasonal = decomposition.seasonal
residual = decomposition.residplt.subplot(411)
plt.plot(ts_log, label='Original')
plt.legend(loc='best')
plt.subplot(412)
plt.plot(trend, label='Trend')
plt.legend(loc='best')
plt.subplot(413)
plt.plot(seasonal,label='Seasonality')
plt.legend(loc='best')
plt.subplot(414)
plt.plot(residual, label='Residuals')
plt.legend(loc='best')
plt.tight_layout()

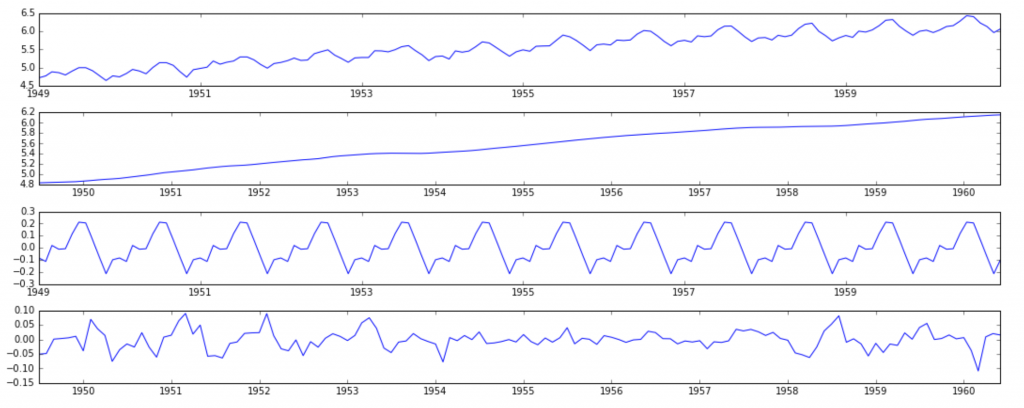
在这里我们可以看到趋势,季节性从数据分离，我们可以建立残差的模型，让我们检查残差的稳定性。

ts_log_decompose = residual
ts_log_decompose.dropna(inplace=True)
test_stationarity(ts_log_decompose)

这样时间序列是非常接近稳定。你也可以尝试高级的分解技术产生更好的结果。同时,你应该注意到, 在这种情况下将残差转换为原始值对未来数据不是很直观。

[Source code for statsmodels.tsa.seasonal]

Note: decomposition = seasonal_decompose(ts_log)

1 如果你的数据的index不是DatetimeIndex而是其它的就会出错

AttributeError: 'Index' object has no attribute 'inferred_freq'

AttributeError: 'Float64Index' object has no attribute 'inferred_freq'

2 如果你的数据的DatetimeIndex不能自动识别出datetime的freq就会出错

ValueError: You must specify a freq or x must be a pandas object with a timeseries index

这时应该手动指定decomposition = seasonal_decompose(ts_log, freq = 1)

3 warnning

VisibleDeprecationWarning: using a non-integer number instead of an integer will result in an error in the future

皮皮blog

时间序列预测

从上我们看到了不同的技术，并且在使得时间序列得以稳定上运作良好。让我们通过差分后建立时间序列模型，因为差分是很受欢迎的技术，也相对更容易添加噪音和季节性从而倒回到预测残差residuals。

在执行趋势和季节性评估技术上,有两种情况：

值之间不含依赖的严格稳定系列。简单的情况下,我们可以建立残差residuals模型作为白噪音（指功率谱密度在整个频域内均匀分布的噪声），但这非常罕见。
序列值之间含有明显依赖。在这种情况下,我们需要使用一些统计模型像ARIMA（差分自回归移动平均模型）来预测数据。

这里简要介绍一下ARIMA，但不会介绍技术细节,但如果你希望更有效地应用它们，你应该理解这些概念的细节。ARIMA代表差分自回归移动平均(Auto-Regressive Integrated Moving Averages)。平稳时间序列的ARIMA预测的只不过是一个线性方程(如线性回归)。

预测依赖于ARIMA模型参数(p d q)

自回归项的数目Number of AR (Auto-Regressive) terms (p)：AR条件仅仅是因变量的滞后。如：如果P等于5，那么预测x（t）将是x（t-1）。。。（t-5）。
移动平均项的数目Number of MA (Moving Average) terms (q):MA条件是预测方程的滞后预测错误。如：如果q等于5，预测x（t）将是e（t-1）。。。e(t-5),e(i)是移动平均叔在第ith个瞬间和实际值的差值。
差分数目Number of Differences (d)：它们是非季节性的差值的数目，即这种情况下我们采用一阶差分。所以传递变量令d=0或者传递原始变量令d=1，两种方法得到的结果一样。

如何确定“p”和“q”的值

我们使用两个坐标来确定这些数字。

自相关函数Autocorrelation Function (ACF)：这是时间序列和它自身滞后版本之间的相关性的测试。比如在自相关函数可以比较时间的瞬间‘t1’…’t2’以及序列的瞬间‘t1-5’…’t2-5’ (t1-5和t2 是结束点)。
部分自相关函数Partial Autocorrelation Function (PACF):这是时间序列和它自身滞后版本之间的相关性测试，但是是在预测（已经通过比较干预得到解释）的变量后。如：滞后值为5，它将检查相关性，但是会删除从滞后值1到4得到的结果。

时间序列（在差分后）的自回归函数和部分自回归函数绘制为:

#ACF and PACF plots:
from statsmodels.tsa.stattools import acf, pacf

lag_acf = acf(ts_log_diff, nlags=20)
lag_pacf = pacf(ts_log_diff, nlags=20, method='ols')

#Plot ACF: 
plt.subplot(121) 
plt.plot(lag_acf)
plt.axhline(y=0,linestyle='--',color='gray')
plt.axhline(y=-1.96/np.sqrt(len(ts_log_diff)),linestyle='--',color='gray')
plt.axhline(y=1.96/np.sqrt(len(ts_log_diff)),linestyle='--',color='gray')
plt.title('Autocorrelation Function')

#Plot PACF:
plt.subplot(122)
plt.plot(lag_pacf)
plt.axhline(y=0,linestyle='--',color='gray')
plt.axhline(y=-1.96/np.sqrt(len(ts_log_diff)),linestyle='--',color='gray')
plt.axhline(y=1.96/np.sqrt(len(ts_log_diff)),linestyle='--',color='gray')
plt.title('Partial Autocorrelation Function')
plt.tight_layout()

Python

此图中,0每一边的两条虚线之间是置信区间。这些可以用来确定“p”和“q”的值:

1、p-部分自相关函数图第一次截断上层置信区间的滞后值。如果你仔细看，该值是p=2。

2、q- 自相关函数图第一次截断上层置信区间的滞后值。如果你仔细看，该值是q=2。

[http://discuss.analyticsvidhya.com/t/seasonal-parameter-in-arima-and-adf-test/7385/1]

现在，考虑个体以及组合效应建立3个不同的ARIMA模型。我也会打印各自的RSS（RSS表示一组统计数据的平方和的平方根）。请注意,这里的RSS是对残差值来说的，而不是实际序列。

首先，我们需要ARIMA模型。

from statsmodels.tsa.arima_model import ARIMA

p,d,q值可以通过ARIMA的order参数即元组(p,d,q)指定。

建立三种情况下的模型：

自回归（AR）模型：

model = ARIMA(ts_log, order=(2, 1, 0))  
results_AR = model.fit(disp=-1)  
plt.plot(ts_log_diff)
plt.plot(results_AR.fittedvalues, color='red')
plt.title('RSS: %.4f'% sum((results_AR.fittedvalues-ts_log_diff)**2))

Python

移动平均数（MA ）模型

model = ARIMA(ts_log, order=(0, 1, 2))  
results_MA = model.fit(disp=-1)  
plt.plot(ts_log_diff)
plt.plot(results_MA.fittedvalues, color='red')
plt.title('RSS: %.4f'% sum((results_MA.fittedvalues-ts_log_diff)**2))

Python

组合模型

model = ARIMA(ts_log, order=(2, 1, 2))  
results_ARIMA = model.fit(disp=-1)  
plt.plot(ts_log_diff)
plt.plot(results_ARIMA.fittedvalues, color='red')
plt.title('RSS: %.4f'% sum((results_ARIMA.fittedvalues-ts_log_diff)**2))

Python

Note: 如果报错TypeError: Cannot cast ufunc subtract output from dtype('float64') to dtype('int64') with casting rule 'same_kind'，说明时序数据的数据类型不是float类型，astype转换一下就可以了。

ARMAResults及其方法[ARMAResults (class in statsmodels.tsa.arima_model)]

在这里我们可以看到,自回归函数模型和移动平均数模型几乎有相同的RSS，但相结合效果显著更好。

倒回到原始区间

现在,我们只剩下最后一步,即把这些值倒回到原始区间。

既然组合模型获得更好的结果，让我们将它倒回原始值，看看它如何执行。

第一步是作为一个独立的序列，存储预测结果并观察。

predictions_ARIMA_diff = pd.Series(results_ARIMA.fittedvalues, copy=True)
print predictions_ARIMA_diff.head()

Python

Note: 1 这些是从‘1949-02-01’开始,而不是第一个月。为什么?这是因为我们将第一个月份取为滞后值，一月前面没有可以减去的元素。

2 这里fittedvalues是已知的数据（或者说是训练数据吧），和[statsmodels.tsa.arima_model.ARMAResults.predict]可以得到相同结果，但是不能是未来的结果。

3 这里只是预测的已有的数据，实际中我们当然是要预测未来的数据。这时应该使用forecast方法，如预测最后时间之后14天的结果：

print(results_ARIMA.forecast(14)[0])

[statsmodels.tsa.arima_model.ARMAResults.forecast]

将差分转换为对数尺度的方法是这些差值连续地添加到基本值。一个简单的方法就是首先确定索引的累计总和,然后将其添加到基本值（这里就是第一个月的值）。

predictions_ARIMA_diff_cumsum = predictions_ARIMA_diff.cumsum()
print predictions_ARIMA_diff_cumsum.head()

Python

你可以在head()使用之前的输出结果进行回算，检查这些是否正确的。接下来我们将它们添加到基本值。为此我们将使用基本值作为所有的值来创建一个序列，并添加差值。

predictions_ARIMA_log = pd.Series(ts_log.ix[0], index=ts_log.index)
predictions_ARIMA_log = predictions_ARIMA_log.add(predictions_ARIMA_diff_cumsum,fill_value=0)
predictions_ARIMA_log.head()

Python

第一个元素是基本值本身，从基本值开始值累计添加。

最后一步是将指数与原序列比较。

predictions_ARIMA = np.exp(predictions_ARIMA_log)
plt.plot(ts)
plt.plot(predictions_ARIMA)
plt.title('RMSE: %.4f'% np.sqrt(sum((predictions_ARIMA-ts)**2)/len(ts)))

Python