全栈工程师开发手册 (作者:栾鹏)
python数据挖掘系列教程
时间序列中常用预测技术,一个时间序列是一组对于某一变量连续时间点或连续时段上的观测值。参考:https://blog.csdn.net/u010414589/article/details/49622625
1. 移动平均法 (MA)
1.1. 简单移动平均法
设有一时间序列y1,y2,…, 则按数据点的顺序逐点推移求出N个数的平均数,即可得到一次移动平均数.
1.2 趋势移动平均法
当时间序列没有明显的趋势变动时,使用一次移动平均就能够准确地反映实际情况,直接用第t周期的一次移动平均数就可预测第1t+周期之值。
时间序列出现线性变动趋势时,用一次移动平均数来预测就会出现滞后偏差。修正的方法是在一次移动平均的基础上再做二次移动平均,利用移动平均滞后偏差的规律找出曲线的发展方向和发展趋势,然后才建立直线趋势的预测模型。故称为趋势移动平均法。
2. 自回归模型(AR)
AR模型是一种线性预测,即已知N个数据,可由模型推出第N点前面或后面的数据(设推出P点).
本质类似于插值,其目的都是为了增加有效数据,只是AR模型是由N点递推,而插值是由两点(或少数几点)去推导多点,所以AR模型要比插值方法效果更好。
3. 自回归滑动平均模型(ARMA)
其建模思想可概括为:逐渐增加模型的阶数,拟合较高阶模型,直到再增加模型的阶数而剩余残差方差不再显著减小为止。
4. GARCH模型
回归模型。除去和普通回归模型相同的之处,GARCH对误差的方差进行了进一步的建模。特别适用于波动性的分析和预测。
5. 指数平滑法
移动平均法的预测值实质上是以前观测值的加权和,且对不同时期的数据给予相同的加权。这往往不符合实际情况。
指数平滑法则对移动平均法进行了改进和发展,其应用较为广泛。
基本思想都是:预测值是以前观测值的加权和,且对不同的数据给予不同的权,新数据给较大的权,旧数据给较小的权。
根据平滑次数不同,指数平滑法分为:一次指数平滑法、二次指数平滑法和三次指数平滑法等。
ARIMA模型
ARIMA模型的全称叫做自回归移动平均模型,全称是(ARIMA, Autoregressive Integrated Moving Average Model)。也记作ARIMA(p,d,q),是统计模型(statistic model)中最常见的一种用来进行时间序列 预测的模型。
1. ARIMA的优缺点
优点: 模型十分简单,只需要内生变量而不需要借助其他外生变量。
缺点:
1.要求时序数据是稳定的(stationary),或者是通过差分化(differencing)后是稳定的。
2.本质上只能捕捉线性关系,而不能捕捉非线性关系。
注意,采用ARIMA模型预测时序数据,必须是稳定的,如果不稳定的数据,是无法捕捉到规律的。比如股票数据用ARIMA无法预测的原因就是股票数据是非稳定的,常常受政策和新闻的影响而波动。
2. 判断是时序数据是稳定的方法。
严谨的定义: 一个时间序列的随机变量是稳定的,当且仅当它的所有统计特征都是独立于时间的(是关于时间的常量)。
判断的方法:
稳定的数据是没有趋势(trend),没有周期性(seasonality)的; 即它的均值,在时间轴上拥有常量的振幅,并且它的方差,在时间轴上是趋于同一个稳定的值的。
可以使用Dickey-Fuller Test进行假设检验。
3. ARIMA的参数与数学形式
ARIMA模型有三个参数:p,d,q。
- p–代表预测模型中采用的时序数据本身的滞后数(lags) ,也叫做AR/Auto-Regressive项
-d–代表时序数据需要进行几阶差分化,才是稳定的,也叫Integrated项。
-q–代表预测模型中采用的预测误差的滞后数(lags),也叫做MA/Moving Average项
先解释一下差分: 假设y表示t时刻的Y的d阶差分。
i f d = 0 , y t = Y t i f d = 1 , y t = Y t − Y t − 1 i f d = 2 , y t = ( Y t − Y t − 1 ) − ( Y t − 1 − Y t − 2 ) = Y t − 2 Y t − 1 + Y t − 2 if \ d=0 ,\ y_t = Y_t \\[2ex] if \ d=1 ,\ y_t = Y_t-Y_{t-1} \\[2ex] if \ d=2 ,\ y_t = (Y_t-Y_{t-1}) -(Y_{t-1}-Y_{t-2}) \\ =Y_t-2Y_{t-1}+Y_{t-2} if d=0, yt=Ytif d=1, yt=Yt−Yt−1if d=2, yt=(Yt−Yt−1)−(Yt−1−Yt−2)=Yt−2Yt−1+Yt−2
ARIMA的预测模型可以表示为:
Y的预测值 = 常量c and/or 一个或多个最近时间的Y的加权和 and/or 一个或多个最近时间的预测误差。
假设p,q,d已知,
ARIMA用数学形式表示为:
y t ^ = μ + ϕ 1 ∗ y t − 1 + . . . + ϕ p ∗ y t − p + θ 1 ∗ e t − 1 + . . . + θ q ∗ e t − q \widehat{y_t} = \mu + \phi_1*y_{t-1} + ...+ \phi_p*y_{t-p} + \theta_1*e_{t-1} +...+\theta_q*e_{t-q} yt =μ+ϕ1∗yt−1+...+ϕp∗yt−p+θ1∗et−1+...+θq∗et−q
其中, ϕ ϕ ϕ表示 A R AR AR的系数, θ θ θ表示 M A MA MA的系数
ARIMA建模基本步骤
获取被观测系统时间序列数据;
对数据绘图,观测是否为平稳时间序列;对于非平稳时间序列要先进行d阶差分运算,化为平稳时间序列;
经过第二步处理,已经得到平稳时间序列。要对平稳时间序列分别求得其自相关系数ACF 和偏自相关系数PACF,通过对自相关图和偏自相关图的分析,得到最佳的阶层 p 和阶数 q
由以上得到的d、q、p,得到ARIMA模型。然后开始对得到的模型进行模型检验。
ARIMA实战解剖
原理大概清楚,实践却还是会有诸多问题,下面就通过Python语言详细解析后三个步骤的实现过程。
文中使用到这些基础库: pandas,numpy,scipy,matplotlib,statsmodels。 对其调用如下
from __future__ import print_function
import pandas as pd
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
import statsmodels.api as sm
from statsmodels.graphics.api import qqplot
3.1 获取数据
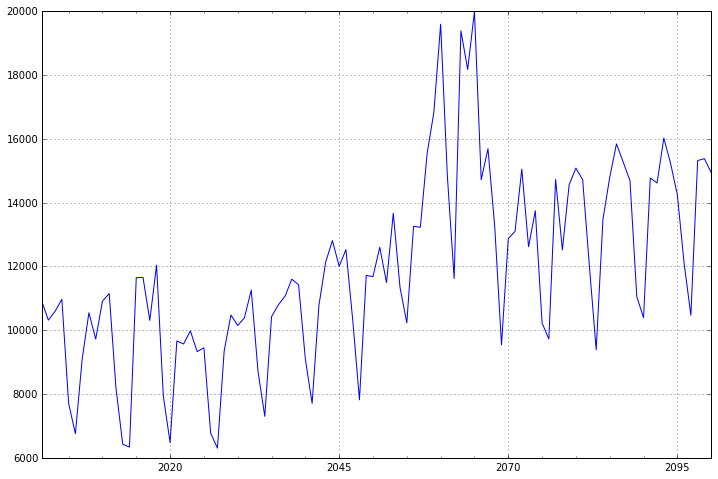
这里我们使用一个具有周期性的测试数据,进行分析。
数据如下:
dta=[10930,10318,10595,10972,7706,6756,9092,10551,9722,10913,11151,8186,6422,
6337,11649,11652,10310,12043,7937,6476,9662,9570,9981,9331,9449,6773,6304,9355,
10477,10148,10395,11261,8713,7299,10424,10795,11069,11602,11427,9095,7707,10767,
12136,12812,12006,12528,10329,7818,11719,11683,12603,11495,13670,11337,10232,
13261,13230,15535,16837,19598,14823,11622,19391,18177,19994,14723,15694,13248,
9543,12872,13101,15053,12619,13749,10228,9725,14729,12518,14564,15085,14722,
11999,9390,13481,14795,15845,15271,14686,11054,10395]dta=pd.Series(dta)
dta.index = pd.Index(sm.tsa.datetools.dates_from_range('2001','2100'))
dta.plot(figsize=(12,8))
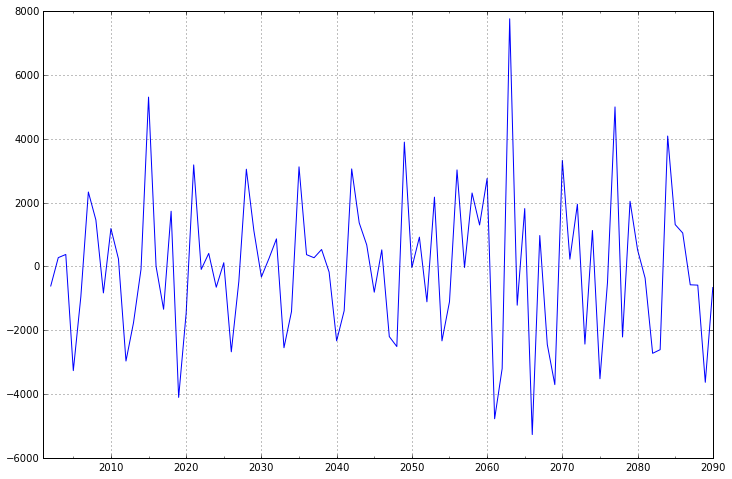
3.2 时间序列的差分d
ARIMA 模型对时间序列的要求是平稳型。因此,当你得到一个非平稳的时间序列时,首先要做的即是做时间序列的差分,直到得到一个平稳时间序列。如果你对时间序列做d次差分才能得到一个平稳序列,那么可以使用ARIMA(p,d,q)模型,其中d是差分次数。
fig = plt.figure(figsize=(12,8))
ax1= fig.add_subplot(111)
diff1 = dta.diff(1)
diff1.plot(ax=ax1)
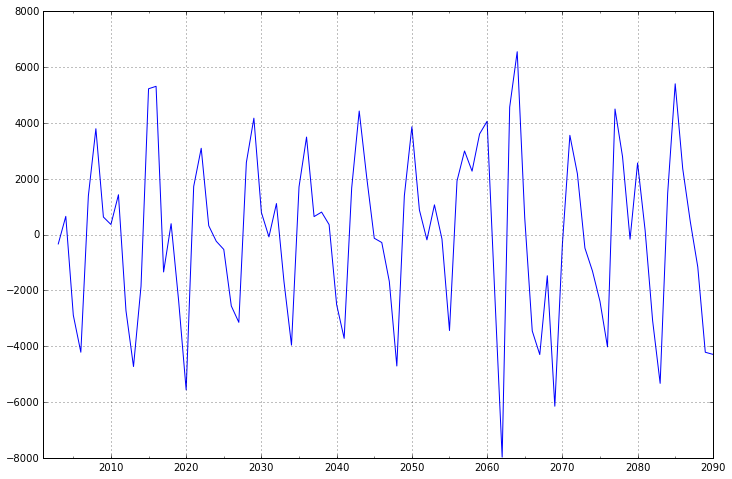
一阶差分的时间序列的均值和方差已经基本平稳,不过我们还是可以比较一下二阶差分的效果
fig = plt.figure(figsize=(12,8))
ax2= fig.add_subplot(111)
diff2 = dta.diff(2)
diff2.plot(ax=ax2)
可以看出二阶差分后的时间序列与一阶差分相差不大,并且二者随着时间推移,时间序列的均值和方差保持不变。因此可以将差分次数d设置为1。
其实还有针对平稳的检验,叫“ADF单位根平稳型检验”,也就是adfuller函数。关于平稳性检测,文章后面会有介绍。
3.3 合适的p,q
现在我们已经得到一个平稳的时间序列,接来下就是选择合适的ARIMA模型,即ARIMA模型中合适的p,q。 文章后面也有介绍如何找到合适的模型阶次p、q。
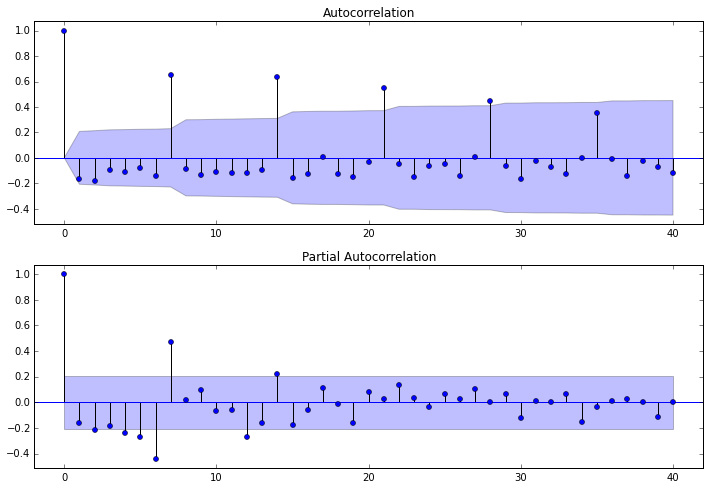
第一步我们要先检查平稳时间序列的自相关图和偏自相关图。因为差分后的序列第一个是NAN,因此要去掉它
dta= dta.diff(1)#我们已经知道要使用一阶差分的时间序列,之前判断差分的程序可以注释掉
fig = plt.figure(figsize=(12,8))
ax1=fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(dta,lags=40,ax=ax1)
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(dta,lags=40,ax=ax2)
其中lags 表示最大滞后的阶数,以上分别得到acf 图和pacf 图
附录:
平稳性检测
方法一:时序图
from pylab import *
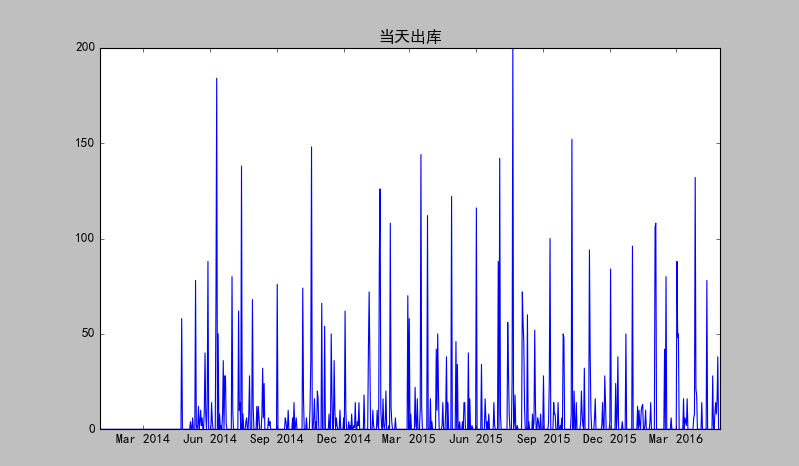
plt.plot(ts)
plt.title(u'当天出库')
show()
序列始终在一个常数值附近随机波动,且波动范围有界,且没有明显的趋势性或周期性,所以可认为是平稳序列。
方法二:自相关图
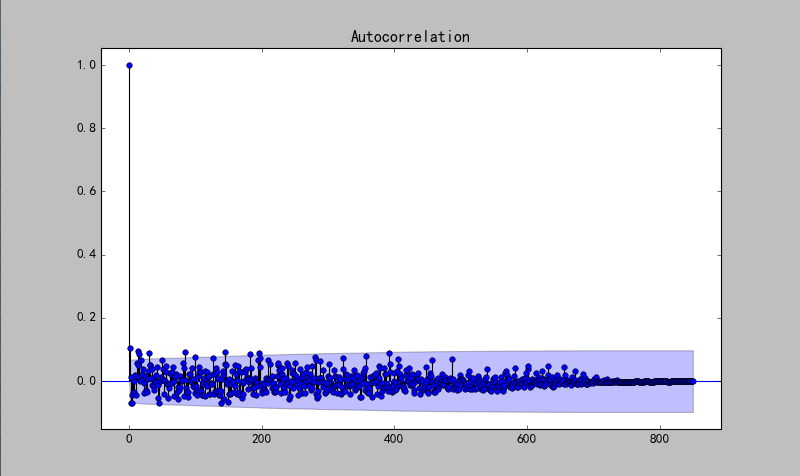
from statsmodels.graphics.tsaplots import plot_pacf,plot_acf
plot_acf(ts)
show()
自相关系数会很快衰减向0,所以可认为是平稳序列。
方法三:ADF单位根检验(精确判断)
temp = np.array(ts)
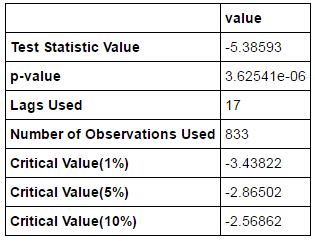
t = sm.tsa.stattools.adfuller(temp) # ADF检验
output=pd.DataFrame(index=['Test Statistic Value', "p-value", "Lags Used", "Number of Observations Used","Critical Value(1%)","Critical Value(5%)","Critical Value(10%)"],columns=['value'])
output['value']['Test Statistic Value'] = t[0]
output['value']['p-value'] = t[1]
output['value']['Lags Used'] = t[2]
output['value']['Number of Observations Used'] = t[3]
output['value']['Critical Value(1%)'] = t[4]['1%']
output['value']['Critical Value(5%)'] = t[4]['5%']
output['value']['Critical Value(10%)'] = t[4]['10%']
output
单位根检验统计量对应的P值远小于0.05,故该序列可确认为平稳序列。
纯随机性检验(白噪声检验)
from statsmodels.stats.diagnostic import acorr_ljungbox
print u'序列的纯随机性检测结果为:',acorr_ljungbox(ts,lags = 1)
输出:
序列的纯随机性检测结果为: (array([ 9.10802245]), array([ 0.00254491]))
P=0.00254491,统计量的P值小于显著性水平0.05,则可以以95%的置信水平拒绝原假设,认为序列为非白噪声序列(否则,接受原假设,认为序列为纯随机序列。)
平稳白噪声和平稳非白噪声序列,适用于ARMA模型。
识别ARMA模型阶次p、q
方法一:ACF、PACF 判断模型阶次
对平稳时间序列Yn,求得其自相关函数(ACF)和偏自相关函数(PACF)序列。
若PACF序列满足在p步截尾,且ACF序列被负指数函数控制收敛到0,则Yn为AR§序列,即p阶的自回归模型。
若ACF序列满足在q步截尾,且PACF序列被负指数函数控制收敛到0,则Yn为MA(q)序列,即q阶的移动平均模型。
若ACF序列和PACF序列满足皆不截尾,但都被负指数函数控制收敛到0,则Yn为ARMA序列。
from statsmodels.graphics.tsaplots import plot_pacf,plot_acf
plot_acf(ts)
plot_pacf(ts)
show()
对于有N个观察值的序列,求得相应于AR§、MA(q) 和 ARMA(p,q)三种模型的残差方差,出现模型最小残差方差时的模型阶数就是各个模型的最佳阶数。
方法二:信息准则定阶
目前选择模型常用如下准则: (其中L为似然函数,k为参数数量,n为观察数)
AIC = -2 ln(L) + 2 k 中文名字:赤池信息量 akaike information criterion
BIC = -2 ln(L) + ln(n)*k 中文名字:贝叶斯信息量 bayesian information criterion
HQ = -2 ln(L) + ln(ln(n))*k hannan-quinn criterion
我们常用的是AIC准则,同时需要尽量避免出现过拟合的情况。所以优先考虑的模型应是AIC值最小的那一个模型。
为了控制计算量,可以限制AR最大阶,MA最大阶。 但是这样带来的坏处是可能为局部最优。
import statsmodels.api as sm
sm.tsa.arma_order_select_ic(ts,max_ar=6,max_ma=4,ic='aic')['aic_min_order'] # AIC
#sm.tsa.arma_order_select_ic(ts,max_ar=6,max_ma=4,ic='bic')['bic_min_order'] # BIC
#sm.tsa.arma_order_select_ic(ts,max_ar=6,max_ma=4,ic='hqic')['hqic_min_order'] # HQIC
一般以AIC准则为准,也可依次尝试每一种准则,选择最优。
添加内容:
RSI:相对强弱指标,用于股票的断线操作预测。
MACD:指数平滑移动平均数,用于股市预测。
KDJ:随机指标,用于期货和股市中短期趋势分析。