【Python计量】自相关性（序列相关性）的检验

article/2025/8/15 4:18:31

文章目录

  • 一、图示法
    • （一）滞后图
    • （二）自相关图
    • （三）自相关图和偏自相关图
  • 二 、DW检验法
  • 三、Breusch-Godfrey检验
    • （一）手动编制函数进行BG检验
    • （二）调用statsmodels的函数进行BG检验
  • 四、Ljung-Box检验

此文章首发于微信公众号：Python for Finance

链接：https://mp.weixin.qq.com/s/BuZg3hY8APHBr_vjmubn5g

多元线性回归模型的基本假设之一就是模型的随机干扰项相互独立或不相关。如果模型的随机干扰项违背了相互独立的基本假设，则称为存在序列相关性（自相关性）。

我们以伍德里奇《计量经济学导论：现代方法》的”第12章 时间序列回归中序列相关和异方差性“的案例12.4为例，使用BARIUM中的数据来进行序列相关性的检验。

import wooldridge as woo
import pandas as pd
import numpy as np
import statsmodels.api as sm
import statsmodels.formula.api as smfbarium = woo.dataWoo('barium')
T = len(barium)
barium.index = pd.date_range(start='1978-02', periods=T, freq='M')reg = smf.ols(formula='np.log(chnimp) ~ np.log(chempi) + np.log(gas) +''np.log(rtwex) + befile6 + affile6 + afdec6',data=barium)
results = reg.fit()
resid = results.resid#获取残差

一、图示法

由于残差 e t e_t et​可以作为扰动项 u t u_t ut​的估计，因此，如果存在序列相关性，必然会由残差项 e t e_t et​反映出来，因此可利用 e t e_t et​的变化图形来判断随机干扰项的序列相关性。

（一）滞后图

滞后图，就是将残差 e t e_t et​和残差滞后n阶的散点图，需要用到pandas的lag_plot函数。

from pandas.plotting import lag_plot

lag_plot函数用法：

lag_plot(series, lag=1, ax=None, **kwds)
主要参数：
series :时间序列数据
lag : 滞后阶数，默认为1
ax : Matplotlib的子图对象，可选

我们绘制残差 e t e_t et​和残差滞后1阶 e t − 1 e_{t-1} et−1​的自相关图，代码如下：

lag_plot(resid, lag=1)
plt.show()

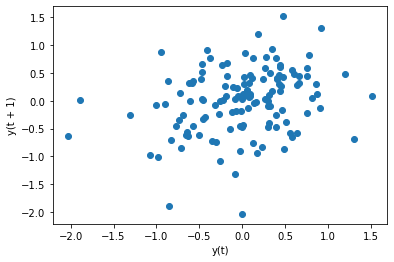
如果我们要绘制残差 e t e_t et​与其滞后1-4阶的图，代码如下：

fig, axes = plt.subplots(1, 4, figsize=(10,3), sharex=True, sharey=True, dpi=100)#1行4列的画布
for i in range(4):lag_plot(resid,lag=i+1, ax=axes[i])axes[i].set_title(f'Lag{i+1}')

结果如下：

（二）自相关图

自相关图的绘制，可以使用pandas库的autocorrelation_plot函数

from pandas.plotting import autocorrelation_plot

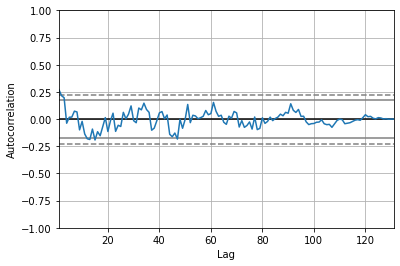
生成图片的横轴是滞后阶数，纵轴是自相关系数。

我们绘制残差项的自相关图，代码如下：

autocorrelation_plot(resid)
plt.show()

（三）自相关图和偏自相关图

自相关系数和偏自相关系数的区别

  • 假设时间序列数据 y t y_t yt​
  • y t = α 0 + α 1 y t − 3 y_t=\alpha_0+\alpha_1y_{t-3} yt​=α0​+α1​yt−3​，这个 α 1 \alpha_1 α1​就是, y t y_t yt​和 y t − 3 y_{t-3} yt−3​的自相关系数。
  • y t = α 0 + α 1 y t − 1 + α 2 y t − 2 + α 3 y t − 3 y_t=\alpha_0+\alpha_1y_{t-1}+\alpha_2y_{t-2}+\alpha_3y_{t-3} yt​=α0​+α1​yt−1​+α2​yt−2​+α3​yt−3​，这个 α 3 \alpha_3 α3​就是, y t y_t yt​和 y t − 3 y_{t-3} yt−3​的偏自相关系数。

自相关图和偏自相关图，建议使用statsmodels包的plot_acf, plot_pacf函数。

from statsmodels.graphics.tsaplots import plot_acf, plot_pacf #自相关图、偏自相关图
import matplotlib.pyplot as plt

plot_acf、plot_pacf函数的参数意义

plot_acf(x, ax=None, lags=None, *, alpha=0.05, use_vlines=True, adjusted=False, fft=False, missing='none', title='Autocorrelation', zero=True, auto_ylims=False, bartlett_confint=True, vlines_kwargs=None, **kwargs)
plot_pacf(x, ax=None, lags=None, alpha=0.05, method=None, use_vlines=True, title='Partial Autocorrelation', zero=True, vlines_kwargs=None, **kwargs)
x：一维的数据序列。
lags：滞后阶数，若未提供，则取np.arange(len(corr))

我们绘制残差项的自相关图，代码如下：

 plot_acf(resid,lags=20) plt.show()

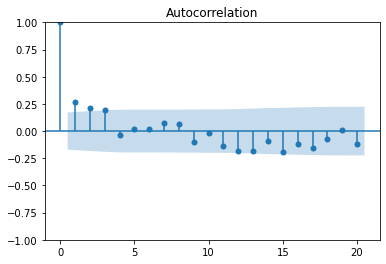
上图反映了resid序列的各阶自相关系数的大小，该图的高度值对应的是各阶自相关系数的值，蓝色区域是95%置信区间，这两条界线是检测自相关系数是否为0时所使用的判别标准：当代表自相关系数的柱条超过这两条界线时，可以认定自相关系数显著不为0。观察上图可知，1、2、3阶的自相关系数都在蓝色范围外，也就是落在了95%置信区间外，所以初步判断该序列可能存在短期的自相关性。

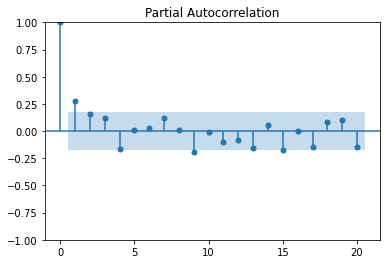
我们还可以绘制出残差项的偏自相关系数图，代码如下：

plot_pacf(resid,lags=20)
plt.show()

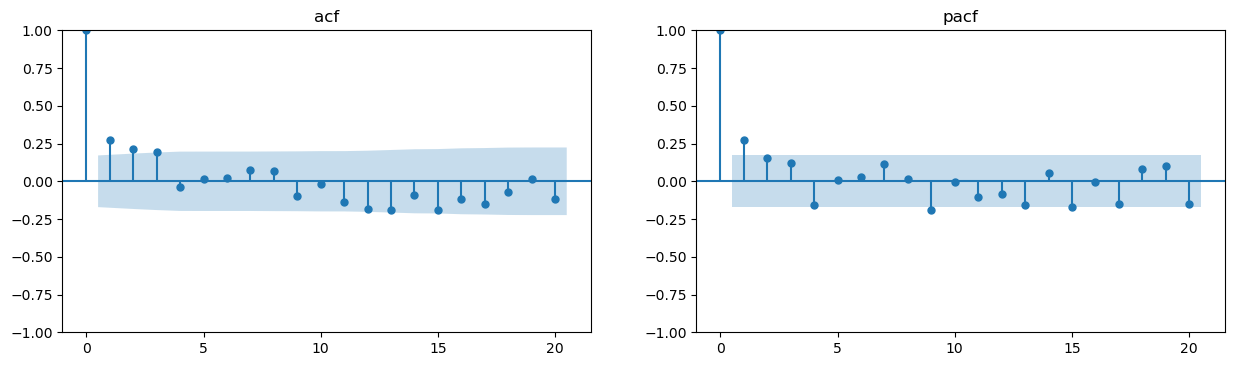
我们若希望将自相关系数图和偏自相关系数图合并成一张图，可以定义函数。

import matplotlib.pyplot as plt
def acf_pacf_plot(timeseries,lags):fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(15, 4), dpi=100)plot_acf(timeseries, lags=lags,ax=axes[0])axes[0].set_title('acf') #设置自相关图标题，也可不设置，采用默认值Autocorrelationplot_pacf(timeseries,lags=lags,ax=axes[1])axes[1].set_title('pacf') #设置偏自相关图标题，也可不设置，采用默认值Partial Autocorrelationplt.show()

若我们需要对残差项做20阶的自相关图、偏自相关图，则调用上述函数即可，参数timeseries设置为resid，参数lags设置为20。

acf_pacf_plot(resid,20)

结果如下：

二 、DW检验法

DW检验是较早提出的自相关检验，现已不常用。它的主要缺点是只能检验一阶自相关，且必须在解释变量满足严格外生性的情况下才成立。

from statsmodels.stats.stattools import durbin_watson
print(f'D-W检验值为{durbin_watson(results.resid)}')
#返回结果：
D-W检验值为1.4584144308481417

三、Breusch-Godfrey检验

BG检验克服了DW检验的缺陷，适合于高阶序列相关及模型中存在滞后被解释变量的情形。

考虑如下多元线性模型：
y t = β 0 + β 1 x t 1 + β 2 x t 2 + . . . + β k x t k + u y_t=\beta_0+\beta_1x_{t1}+\beta_2x_{t2}+...+\beta_kx_{tk}+u yt​=β0​+β1​xt1​+β2​xt2​+...+βk​xtk​+u
若怀疑随机干扰项存在p阶序列相关：
u t = ρ 1 u t − 1 + ρ 2 u t − 2 + . . . + ρ p u t − p + ε t u_t=\rho_1u_{t-1}+\rho_2u_{t-2}+...+\rho_pu_{t-p}+\varepsilon_t ut​=ρ1​ut−1​+ρ2​ut−2​+...+ρp​ut−p​+εt​
检验原假设：
H 0 : ρ 1 = ρ 2 = . . . = ρ p = 0 H_0:\rho_1=\rho_2=...=\rho_p=0 H0​:ρ1​=ρ2​=...=ρp​=0
由于 u t u_t ut​不可测，故用 e t e_t et​替代，并引入解释变量，进行如下辅助回归：
e t = γ 1 x t 1 + γ 2 x t 2 + . . . + γ k x t k + δ 1 e t − 1 + δ 2 e t − 2 + . . . + δ p e t − p + ε t e_t=\gamma_1x_{t1}+\gamma_2x_{t2}+...+\gamma_kx_{tk}+\delta_1e_{t-1}+\delta_2e_{t-2}+...+\delta_pe_{t-p}+\varepsilon_t et​=γ1​xt1​+γ2​xt2​+...+γk​xtk​+δ1​et−1​+δ2​et−2​+...+δp​et−p​+εt​
无自相关的原假设相当于检验：
H 0 : γ 1 = γ 2 = . . . = γ p = 0 H_0:\gamma_1=\gamma_2=...=\gamma_p=0 H0​:γ1​=γ2​=...=γp​=0
BG检验的步骤：

（1）将 y t y_t yt​对 x t 1 x_{t1} xt1​, x t 2 x_{t2} xt2​,…, x t k x_{tk} xtk​做回归，求出OLS残差 e t e_t et​

（2）将 e t e_t et​对 x t 1 x_{t1} xt1​, x t 2 x_{t2} xt2​,…, x t k x_{tk} xtk​, e t − 1 e_{t-1} et−1​, e t − 2 e_{t-2} et−2​,…, e t − p e_{t-p} et−p​做回归

（3）计算 e t − 1 e_{t-1} et−1​, e t − 2 e_{t-2} et−2​,…, e t − p e_{t-p} et−p​联合显著的F检验

（一）手动编制函数进行BG检验

barium['resid'] = results.resid
barium['resid_lag1'] = barium['resid'].shift(1)
barium['resid_lag2'] = barium['resid'].shift(2)
barium['resid_lag3'] = barium['resid'].shift(3)reg_manual = smf.ols(formula='resid~ np.log(chempi) + np.log(gas) +''np.log(rtwex) + befile6 + affile6 + afdec6+''resid_lag1 + resid_lag2 + resid_lag3', data=barium)
results_manual = reg_manual.fit()hypotheses = ['resid_lag1 = 0', 'resid_lag2 = 0', 'resid_lag3 = 0']
ftest_manual = results_manual.f_test(hypotheses)
F_statistic = ftest_manual.fvalue
F_pval = ftest_manual.pvalue
print(f'BG检验的F统计量: {F_statistic}')
print(f'BG检验的p值: {F_pval}')'''
BG检验的F统计量: 5.122907054069363
BG检验的p值: 0.0022898028329663344
'''

我们可以查看辅助回归的回归结果：

print(results_manual.summary())
'''OLS Regression Results                            
==============================================================================
Dep. Variable:                  resid   R-squared:                       0.116
Model:                            OLS   Adj. R-squared:                  0.048
Method:                 Least Squares   F-statistic:                     1.719
Date:                Sat, 14 May 2022   Prob (F-statistic):             0.0920
Time:                        09:28:33   Log-Likelihood:                -104.56
No. Observations:                 128   AIC:                             229.1
Df Residuals:                     118   BIC:                             257.6
Df Model:                           9                                         
Covariance Type:            nonrobust                                         
==================================================================================coef    std err          t      P>|t|      [0.025      0.975]
----------------------------------------------------------------------------------
Intercept        -14.3691     20.656     -0.696      0.488     -55.273      26.535
np.log(chempi)    -0.1432      0.472     -0.303      0.762      -1.078       0.792
np.log(gas)        0.6233      0.886      0.704      0.483      -1.131       2.378
np.log(rtwex)      0.1787      0.391      0.457      0.649      -0.596       0.953
befile6           -0.0859      0.251     -0.342      0.733      -0.583       0.411
affile6           -0.1221      0.255     -0.479      0.632      -0.626       0.382
afdec6            -0.0668      0.274     -0.244      0.808      -0.610       0.476
resid_lag1         0.2215      0.092      2.417      0.017       0.040       0.403
resid_lag2         0.1340      0.092      1.454      0.148      -0.048       0.317
resid_lag3         0.1255      0.091      1.378      0.171      -0.055       0.306
==============================================================================
Omnibus:                        6.375   Durbin-Watson:                   1.947
Prob(Omnibus):                  0.041   Jarque-Bera (JB):                5.978
Skew:                          -0.444   Prob(JB):                       0.0503
Kurtosis:                       3.576   Cond. No.                     9.78e+03
==============================================================================Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 9.78e+03. This might indicate that there are
strong multicollinearity or other numerical problems.
'''

由于辅助回归使用了 e t − p e_{t-p} et−p​损失了p个样本观测值，故样本容量仅有 ( n − p ) (n-p) (n−p)。Davidson and MacKinnon(1993)建议，把残差中因滞后而缺失的项用其期望值0来代替，以保持样本容量为n。

则代码修改为：

barium['resid'] = results.resid
barium['resid_lag1'] = barium['resid'].shift(1).fillna(0) #将残差缺失项用0来代替
barium['resid_lag2'] = barium['resid'].shift(2).fillna(0) #将残差缺失项用0来代替
barium['resid_lag3'] = barium['resid'].shift(3).fillna(0) #将残差缺失项用0来代替reg_manual = smf.ols(formula='resid~ np.log(chempi) + np.log(gas) +''np.log(rtwex) + befile6 + affile6 + afdec6+''resid_lag1 + resid_lag2 + resid_lag3', data=barium)
results_manual = reg_manual.fit()hypotheses = ['resid_lag1 = 0', 'resid_lag2 = 0', 'resid_lag3 = 0']
ftest_manual = results_manual.f_test(hypotheses)
F_statistic = ftest_manual.fvalue
F_pval = ftest_manual.pvalue
print(f'BG检验的F统计量: {F_statistic}')
print(f'BG检验的p值: {F_pval}')'''
BG检验的F统计量: 5.124662239772509
BG检验的p值: 0.002263719767131574
'''

我们可以查看辅助回归的回归结果：

print(results_manual.summary())
'''OLS Regression Results                            
==============================================================================
Dep. Variable:                  resid   R-squared:                       0.113
Model:                            OLS   Adj. R-squared:                  0.047
Method:                 Least Squares   F-statistic:                     1.708
Date:                Sat, 14 May 2022   Prob (F-statistic):             0.0942
Time:                        09:26:57   Log-Likelihood:                -106.95
No. Observations:                 131   AIC:                             233.9
Df Residuals:                     121   BIC:                             262.7
Df Model:                           9                                         
Covariance Type:            nonrobust                                         
==================================================================================coef    std err          t      P>|t|      [0.025      0.975]
----------------------------------------------------------------------------------
Intercept        -13.1407     20.351     -0.646      0.520     -53.431      27.149
np.log(chempi)    -0.0435      0.457     -0.095      0.924      -0.948       0.862
np.log(gas)        0.5436      0.876      0.621      0.536      -1.190       2.277
np.log(rtwex)      0.2024      0.386      0.525      0.601      -0.561       0.966
befile6           -0.0815      0.251     -0.325      0.746      -0.578       0.415
affile6           -0.1243      0.254     -0.489      0.626      -0.628       0.379
afdec6            -0.0776      0.274     -0.283      0.777      -0.619       0.464
resid_lag1         0.2186      0.090      2.416      0.017       0.039       0.398
resid_lag2         0.1341      0.092      1.458      0.147      -0.048       0.316
resid_lag3         0.1257      0.091      1.381      0.170      -0.054       0.306
==============================================================================
Omnibus:                        5.672   Durbin-Watson:                   1.955
Prob(Omnibus):                  0.059   Jarque-Bera (JB):                5.196
Skew:                          -0.414   Prob(JB):                       0.0744
Kurtosis:                       3.516   Cond. No.                     9.76e+03
==============================================================================Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 9.76e+03. This might indicate that there are
strong multicollinearity or other numerical problems.
'''

（二）调用statsmodels的函数进行BG检验

从statsmodels库的stats子模块的diagnostic工具中导入acorr_breusch_godfrey

from statsmodels.stats.diagnostic import acorr_breusch_godfrey #BG检验

acorr_breusch_godfrey函数的参数意义及返回结果

acorr_breusch_godfrey(res, nlags=None, store=False)
参数介绍：
res : 回归结果，对该模型的残差进行自相关检验。
nlags : 滞后阶数
store : 默认为False；若为True，则会返回ResultsStore返回值：
lm : LM统计量值
lm_pvalue : LM统计量的p值，若p值小于显著性水平，则拒绝无自相关性的原假设，即存在自相关性
fvalue : F统计量值       
f_pvalue : F统计量对应的p值，若p值小于显著性水平，则拒绝无自相关性的原假设，即存在自相关性
res_store：ResultsStore，若store为True则返回

Davidson and MacKinnon(1993)建议，把残差中因滞后而缺失的项用其期望值0来代替，以保持样本容量为n。acorr_breusch_godfrey函数采用的是Davidson-MacKinnon方法。

对上述模型做BG检验，代码如下：

bg_result = acorr_breusch_godfrey(results,nlags=3) 
bg_lm_statistic = bg_result[0]
bg_lm_pval = bg_result[1]
bg_F_statistic= bg_result[2] 
bg_F_pval = bg_result[3]
bg_test_output=pd.Series(bg_result[0:4],index=['bg_lm_statistic','bg_lm_pval','bg_F_statistic','bg_F_pval'])   
print(bg_test_output)'''
bg_lm_statistic    14.768156
bg_lm_pval          0.002026
bg_F_statistic      5.124662
bg_F_pval           0.002264
dtype: float64
'''

同时，我们可以查看BG检验的辅助回归模型结果：

print(bg_result[4].resols.summary())
'''OLS Regression Results                            
==============================================================================
Dep. Variable:                      y   R-squared:                       0.113
Model:                            OLS   Adj. R-squared:                  0.047
Method:                 Least Squares   F-statistic:                     1.708
Date:                Fri, 13 May 2022   Prob (F-statistic):             0.0942
Time:                        20:26:10   Log-Likelihood:                -106.95
No. Observations:                 131   AIC:                             233.9
Df Residuals:                     121   BIC:                             262.7
Df Model:                           9                                         
Covariance Type:            nonrobust                                         
==============================================================================coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const         -6.5703     10.175     -0.646      0.520     -26.715      13.575
x1            -0.0435      0.457     -0.095      0.924      -0.948       0.862
x2             0.5436      0.876      0.621      0.536      -1.190       2.277
x3             0.2024      0.386      0.525      0.601      -0.561       0.966
x4            -0.0815      0.251     -0.325      0.746      -0.578       0.415
x5            -0.1243      0.254     -0.489      0.626      -0.628       0.379
x6            -0.0776      0.274     -0.283      0.777      -0.619       0.464
x7            -6.5703     10.175     -0.646      0.520     -26.715      13.575
x8             0.2186      0.090      2.416      0.017       0.039       0.398
x9             0.1341      0.092      1.458      0.147      -0.048       0.316
x10            0.1257      0.091      1.381      0.170      -0.054       0.306
==============================================================================
Omnibus:                        5.672   Durbin-Watson:                   1.955
Prob(Omnibus):                  0.059   Jarque-Bera (JB):                5.196
Skew:                          -0.414   Prob(JB):                       0.0744
Kurtosis:                       3.516   Cond. No.                     7.48e+16
==============================================================================Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The smallest eigenvalue is 1.33e-29. This might indicate that there are
strong multicollinearity problems or that the design matrix is singular.
'''

acorr_breusch_godfrey函数做辅助回归的因变量为残差项，自变量为[1,A,1,B]，其中A为解释变量，B为残差滞后项。

在以上回归结果中，y代表残差项，x1-x6代表解释变量，x8-x10代表残差滞后项，(const+x7)代表常数项。

我们可以在acorr_breusch_godfrey函数的基础上，编制一个能返回自相关性检验结果的函数。

def bg_test(results,nlags):bg_result = acorr_breusch_godfrey(results,nlags=3) bg_lm_statistic = bg_result[0]bg_lm_pval = bg_result[1]bg_F_statistic= bg_result[2] bg_F_pval = bg_result[3]bg_test_output=pd.Series(bg_result[0:4],index=['bg_lm_statistic','bg_lm_pval','bg_F_statistic','bg_F_pval'])   return bg_test_output

#失败，先放着。同时，我们可以编制一个函数，可以

p_value_threshold=0.1
autocorrelation_results = pd.DataFrame(columns=['Autocorrelation test', 'lag', 'p-value', 'outcome']
for i in range(0, 5):lag=i+1bg_F_pval = acorr_breusch_godfrey(results, nlags=lag)[3]autocorrelation_results.iloc[i] = ['Breusch-Godfrey', lag, bg_F_pval, 'Pass' if bg_F_pval> p_value_threshold else 'Fail']

四、Ljung-Box检验

LB检验：

  • H0假设：序列的每个值是独立的，即纯随机
  • HA假设：序列之间不是独立的，即存在相关性

从statsmodels库的stats子模块的diagnostic工具中导入acorr_ljungbox

from statsmodels.stats.diagnostic import acorr_ljungbox #LB检验

acorr_ljungbox函数的参数意义及返回结果

acorr_ljungbox(x, lags=None, boxpierce=False, model_df=0, period=None, return_df=True, auto_lag=False)
y : 一维的数据序列
lags:滞后阶数，若lags为整数，则会对[1,lags]区间的所有滞后阶数做LB检验；若lags为列表，则只展示列表内的滞后阶数的LB检验结果。
boxpierce：默认False,为True时表示除返回LB统计量还会返回Box和Pierce的Q统计量返回结果为：
lbvalue: Ljung-Box检验统计量
pvalue: Ljung-Box检验统计量对应的p值，若p值小于显著性水平，则拒绝纯随机序列的原假设，即序列不是纯随机序列
bpvalue:Box-Pierce检验统计量
bppvalue: Box-Pierce检验统计量对应的p值，若p值小于显著性水平，则拒绝纯随机序列的原假设

对上述模型做LB检验，代码如下：

print(acorr_ljungbox(results.resid, lags=[10])) #对10阶做LB检验
'''lb_stat  lb_pvalue
10  24.445298   0.006502
'''
print(acorr_ljungbox(results.resid, lags=10)) #对1-10阶均做LB检验
'''lb_stat  lb_pvalue
1    9.821711   0.001725
2   16.072867   0.000323
3   21.332651   0.000090
4   21.532752   0.000248
5   21.571232   0.000632
6   21.619047   0.001419
7   22.365714   0.002197
8   22.973536   0.003398
9   24.381012   0.003738
10  24.445298   0.006502
'''

LB检验的p值小于0.01, 则拒绝纯随机序列的原假设，即序列不是纯随机序列。

参考文献：

Python时间序列分析https://www.machinelearningplus.com/time-series/time-series-analysis-python/

Python与时间序列https://blog.csdn.net/yuanzhoulvpi/article/details/120384708


http://chatgpt.dhexx.cn/article/yVTrEWCn.shtml

相关文章

计量经济学笔记6-Eviews操作-自相关的检验与消除（DW、LM检验与FGLS、广义差分变换）

计量经济学笔记6-Eviews操作-自相关的检验与消除（DW、LM检验与FGLS、广义差分变换）

完成期末作业的同时来更一下博客 背景介绍 对中国储蓄存款总额（Y，亿元）与GDP（亿元）两个变量进行一元线性回归，检验并消除自相关。 自相关分为一阶自相关和高阶自相关，通常使用DW检验来查看是…
阅读更多...
应用回归分析（知识点整理）（四）——SPSS处理自相关（序列相关）

应用回归分析（知识点整理）（四）——SPSS处理自相关（序列相关）

文章目录 自相关自相关产生的原因自相关产生的后果自相关的检验方法图示检验法自相关系数法DW（杜宾沃森）检验 自相关的消除迭代法差分法SPSS处理自相关示例 自相关 自相关产生的原因 （1）忽略遗漏了关键变量 （2&#…
阅读更多...
计量经济学笔记——自相关的检验和处理（转载）

计量经济学笔记——自相关的检验和处理（转载）

自相关（序列相关）;线性相关模型中的随机误差项的各期望值之间存在相关关系 如果随机干扰项之间不存在自相关，εt和εts的协方差为0 序列相关的形式：1）一阶序列相关：干扰项只与其滞后一期值相关 2&#xff0…
阅读更多...
线性回归:自相关检测及其处理方法

线性回归:自相关检测及其处理方法

1 自相关的定义 1.1 定义 对于线性回归模型 Y i β 0 β 1 X 1 i β 2 X 2 i ⋯ β n X n i u i Y_{i}\beta_{0}\beta_{1}X_{1i}\beta_{2}X_{2i}\dots\beta_{n}X{ni}u_{i} Yi​β0​β1​X1i​β2​X2i​⋯βn​Xniui​在其他经典假定不变的条件下，若 C o v …
阅读更多...
相同数相乘

相同数相乘

#include <stdio.h> int main() { long term0,sum0; int a,i,n; printf("input a,n:"); scanf("%d,%d",&a,&n); for(i1;i<n;i) { termterm*10a; sumsumterm; } printf("sum%1d\n",sum); }
阅读更多...
学习C语言——任意两个数相乘

学习C语言——任意两个数相乘

阅读更多...
实现两个矩阵相乘

实现两个矩阵相乘

题目&#xff1a;实现两个矩阵相乘。 想法&#xff1a; 通过分析矩阵相乘可假设变量i,j,k控制下标&#xff0c; 则有以下公式&#xff1a; c[i][j]a[i][k]*b[k][j]&#xff08;三个变量循环次数&#xff1a;i>j>k&#xff09; 所以可以使用三次循环解出相乘的每个数…
阅读更多...
c++两个特别大的数之间相乘怎么计算？

c++两个特别大的数之间相乘怎么计算？

两个数特别大&#xff0c;相乘起来超过了long int型的范围&#xff1f;怎么计算&#xff1f; 比如&#xff1a;要计算123456789987654321 * 987654321123456的值&#xff0c;怎么写程序&#xff1f; /* large_num_operation.cpp */ #include <iostream> #include <cst…
阅读更多...
两个整数相乘的java实现

两个整数相乘的java实现

package 乘法; /* 求 345*7893 4 5X7 8 9———————————————————————— */ public class Chengfa { public static void main(String[] args) {//乘数1 将两个乘数分别出入两个数组中&#xff0c;//数组中的元素对应的位置分别是个位 十位 百位 数组[…
阅读更多...
在Java中实现两数相乘

在Java中实现两数相乘

要实现两数相乘算总额&#xff1a;input1.value() * input2.value() 如果直接获取到两个input值相乘&#xff0c;那么结果就有一点点小偏差&#xff0c;是因为精度缺失 $("#totalSum").val(input1.value() * input2.value()); Js代码&#xff1a; //期初库存 按钮…
阅读更多...
两整数相乘算法

两整数相乘算法

算法需求 求两个整数相乘的算法 算法分析 将前一个数的每一位和后一个数的每一位相乘&#xff0c;因计算过程中涉及到满十进位的问题&#xff0c;所以可以通过判断相乘数的位数进行补零操作来简化这个问题&#xff0c;如下图所示&#xff1a; 例如计算&#xff1a;84 * 13…
阅读更多...
C++实现——两个大数相乘

C++实现——两个大数相乘

#include <iostream> #include <vector> #include <string> using namespace std; //大数相乘 /** *num1 乘数1 *num2 乘数2 *return 结果字符串 */ string BigMutiple(string num1, string num2){string res"";//两个数的位数int m num1.size(),…
阅读更多...
两两相乘求和

两两相乘求和

给定 n 个整数 a_1, a_2, , a_na1​,a2​,⋅⋅⋅,an​ &#xff0c;求它们两两相乘再相加的和&#xff0c;即&#xff1a; 输入格式 输入的第一行包含一个整数 n。 第二行包含 n 个整数。 输出格式 输出一个整数 S&#xff0c;表示所求的和。请使用合适的数据类型进行运…
阅读更多...
php 订单自动售货 实现,PHP自动售货发卡网源码 集成多种支付接口

php 订单自动售货 实现,PHP自动售货发卡网源码 集成多种支付接口

支付接口已集成 支付宝当面付 支付宝PC支付 支付宝手机支付 payjs微信扫码. Paysapi(支付宝/微信). 码支付(QQ/支付宝/微信) 微信企业扫码支付 全网易支付支持(针对彩虹版) 基本环境要求 (PHP PHPCLI) version > 7.0 Nginx version > 1.16 MYSQL version > 5.6 Redis…
阅读更多...
php如何做7天后自动售货店,PHP自动售货发卡网源码集成多种支付接口

php如何做7天后自动售货店,PHP自动售货发卡网源码集成多种支付接口

PHP自动售货发卡网源码 集成多种支付接口 支付接口已集成 支付宝当面付 支付宝PC支付 支付宝手机支付 payjs微信扫码. Paysapi(支付宝/微信). 码支付(QQ/支付宝/微信) 微信企业扫码支付 全网易支付支持(针对彩虹版)基本环境要求 (PHP PHPCLI) version > 7.0 Nginx version …
阅读更多...
独角数卡PHP自动化售货发卡网源码下载

独角数卡PHP自动化售货发卡网源码下载

源码下载&#xff1a;独角数卡PHP自动化售货发卡网源码-小程序文档类资源-CSDN下载 独角数卡PHP自动化售货发卡网源码 支付接口已集成 支付宝当面付 支付宝PC支付 支付宝手机支付 payjs微信扫码. Paysapi(支付宝/微信). 码支付(QQ/支付宝/微信) 微信企业扫码支付 全网易支付支…
阅读更多...
php电商实现自动售货,2020PHP自动售货发卡网程序开源源码 集成多个支付接口

php电商实现自动售货,2020PHP自动售货发卡网程序开源源码 集成多个支付接口

支付接口已集成 支付宝当面付 支付宝PC支付 支付宝手机支付 payjs微信扫码. Paysapi(支付宝/微信). 码支付(QQ/支付宝/微信) 微信企业扫码支付 全网易支付支持(针对彩虹版) 基本环境要求 (PHP PHPCLI) version > 7.0 Nginx version > 1.16 MYSQL version > 5.6 Redis …
阅读更多...
个人开发者只要一行代码接入微信支付和支付宝支付

个人开发者只要一行代码接入微信支付和支付宝支付

接入支付功能 对于个人开发者来说&#xff0c;我们很希望我们开发的App被广泛使用&#xff0c;同时可以获得一些额外收入&#xff0c;那就更好了。但是在微信开放平台或者支付宝开放平台申请支付功能&#xff0c;需要是企业才可以接入&#xff0c;对于我们个人开发者来说&#…
阅读更多...
php皮肤程序,2020修复升级版PHP全新皮肤界面点赞任务系统平台源码运营版,仿众人帮蚂蚁帮扶牛帮...

php皮肤程序,2020修复升级版PHP全新皮肤界面点赞任务系统平台源码运营版,仿众人帮蚂蚁帮扶牛帮...

【温馨提示】源码包解压密码&#xff1a;www.youhutong.com 资源描述 2020修复升级版PHP全新皮肤界面点赞任务系统平台源码运营版,仿众人帮蚂蚁帮扶牛帮 测试环境&#xff1a; php5.6apache2.4mysq5.6 源码介绍&#xff1a; 优化前台UI 及任务功能 前台用户可发布任务【老款只能…
阅读更多...
个人支付方案（免签约）-支付宝当面付

个人支付方案（免签约）-支付宝当面付

背景 作者作为个人开发者&#xff0c;想接入支付功能&#xff0c;所以了解了下目前支付相关的方案&#xff0c;发现大体有以下几种&#xff08;参见xpay&#xff09;&#xff1a; 支付宝和微信官方支付接口&#xff1a;基本都需要企业资格才能开通&#xff0c;最起码也要是个…
阅读更多...
推荐文章

Copyright @ 2022~2023