两整数相乘算法

article/2025/8/15 4:18:34

算法需求

求两个整数相乘的算法

算法分析

将前一个数的每一位和后一个数的每一位相乘，因计算过程中涉及到满十进位的问题，所以可以通过判断相乘数的位数进行补零操作来简化这个问题，如下图所示：
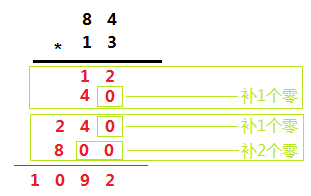
在这里插入图片描述

例如计算：84 * 13
第一步计算4 * 13：
4 * 3 = 12（3在个位，不需要补零）
4 * 1 = 4 （1在十位，计算结果需要补1个零，即4*10）
结果：(4 * 1 * 10) + (4 * 3) = 52（4在个位，计算结果不需要补零）

第二步计算8 * 13：
8 * 3 = 24（3在个位，不需要补零）
8 * 1 = 8（1在十位，需要补1个零，即8*10）
结果：(8 * 1 * 10 + 8 * 3) * 10 = 1040（8在十位，计算结果需要补1个零）

最后一步：把上述几步结果值相加
结果：1040 + 52 = 1092

代码实现

// 乘法操作
public static long mutilply(String left, String right) {char[] leftAry = left.toCharArray();char[] rightAry = right.toCharArray();long num = 0;// 第二轮叠加所有的数for (int i = leftAry.length - 1; i >= 0; i--) {long total = 0;int startInt = leftAry[i] - '0';// 第一轮叠加所有的数for (int j = rightAry.length - 1; j >= 0; j--) {int result = 0;int endInt = rightAry[j] - '0';result = startInt * endInt;// 补零操作long buildNum = fillZero(rightAry.length - j - 1);total += result * buildNum;}long buildNum = fillZero(leftAry.length - i - 1);num += total * buildNum;}return num;
}// 补零操作
private static long fillZero(int n) {StringBuilder builder = new StringBuilder();builder.append("1");for (int i = 0; i < n; i++) {builder.append("0");}return Long.parseLong(builder.toString());
}