梯度下降法

最优化问题是求解函数极值的问题，包括极大值和极小值。相信所有的读者对这个问题都不陌生，在初中时我们就学会了求解二次函数的极值（抛物线的顶点），高中时学习了幂函数，指数函数，对数函数，三角函数，反三角函数等各种类型的函数，求函数极值的题更是频频出现。这些方法都采用了各种各样的技巧，没有一个统一的方案。

真正的飞跃发生在大学时，微积分为我们求函数的极值提供了一个统一的思路：找函数的导数等于0的点，因为在极值点处，导数必定为0。这样，只要函数的可导的，我们就可以用这个万能的方法解决问题，幸运的是，在实际应用中我们遇到的函数基本上都是可导的。

在机器学习之类的实际应用中，我们一般将最优化问题统一表述为求解函数的极小值问题，即：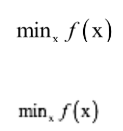
其中x称为优化变量，f称为目标函数。极大值问题可以转换成极小值问题来求解，只需要将目标函数加上负号即可：

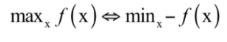
有些时候会对优化变量x有约束，包括等式约束和不等式约束，它们定义了优化变量的可行域，即满足约束条件的点构成的集合。在这里我们先不考虑带约束条件的问题。

一个优化问题的全局极小值$X^{\ast }$是指对于可行域里所有的x，有：

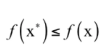
即全局极小值点处的函数值不大于任意一点处的函数值。局部极小值$X^{\ast }$定义为存在一个$\delta$邻域，对于在邻域内：

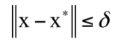
并且在可行域内的所有x，有：

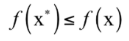
即局部极小值点处的函数值比一个局部返回内所有点的函数值都小。在这里，我们的目标是找到全局极小值。不幸的是，有些函数可能有多个局部极小值点，因此即使找到了导数等于0的所有点，还需要比较这些点处的函数值。

导数与梯度

由于实际应用中一般都是多元函数，因此我们跳过一元函数，直接介绍多元函数的情况。梯度是导数对多元函数的推广，它是多元函数对各个自变量偏导数形成的向量。多元函数的梯度定义为：

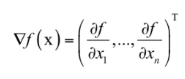
「正定矩阵」和「半正定矩阵」

1 基本的定义

正定和半正定这两个词的英文分别是positive definite和positive semi-definite，其中，definite是一个形容词，表示“明确的、确定的”等意思。
初学线性代数的读者可能会被这两个词“唬住”，但正定矩阵和半正定矩阵的定义实际上是很简单的 (不考虑复数构成的矩阵)：

【定义1】给定一个大小为$n\times n$的实对称矩阵$A$ ，若对于任意长度为$n$的非零向量$x$，有$x^{T}Ax>0$恒成立，则矩阵$A$是一个正定矩阵。

【定义2】给定一个大小为 [公式] 的实对称矩阵$n\times n$，若对于任意长度为$A$ 的向量$x$，有 [公式] 恒成立，则矩阵$x^{T}Ax\ge 0$是一个半正定矩阵。

根据正定矩阵和半正定矩阵的定义，我们也会发现：半正定矩阵包括了正定矩阵，与非负实数 (non-negative real number)和正实数 (positive real number)之间的关系很像。

从二次函数到正定/半正定矩阵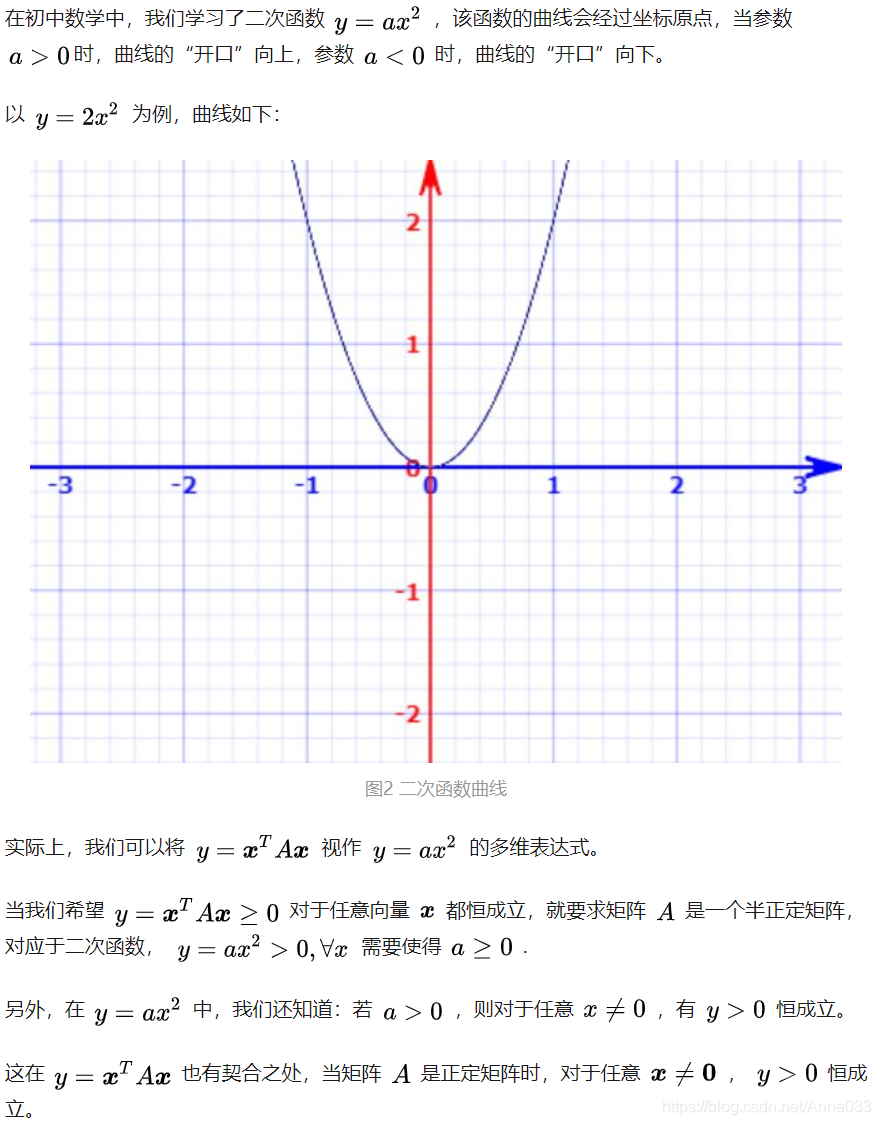

正定矩阵和半正定矩阵的直观解释

为什么协方差矩阵要是半正定的？

最速下降法

1 解决的问题

最速梯度下降法解决的问题是无约束优化问题，而所谓的无约束优化问题就是对目标函数的求解，没有任何的约束限制的优化问题，比如求下方最小值：$minf(x)$
其中的函数$f:R^n\to R$.
求解这类的问题可以分为两大类：一个是最优条件法和迭代法。
最优条件法是是指当函数存在解析形式，能够通过最优性条件求解出显式最优解。对于无约束最优化问题，如果f(x)在最优点x附近可微，那么x是局部极小点的必要条件为： [公式] 我们常常就是通过这个必要条件去求取可能的极小值点，再验证这些点是否真的是极小值点。当上式方程可以求解的时候，无约束最优化问题基本就解决了。
实际中，这个方程往往难以求解。这就引出了第二大类方法：迭代法。

2 最速梯度下降法

3 最速梯度下降法直观理解

第一步

迭代法的初始点选择。

第二步

第三步

这步在是在选取迭代方向，也就是从当前点迭代的方向。这里选取当前点的梯度负方向，为什么选择这个方向，是因为梯度的负方向是局部下降最快的方向，这里不详细证明，可以参考我以前的一个回答：为什么梯度反方向是函数值局部下降最快的方向？https://zhuanlan.zhihu.com/p/24913912

第四步

第四步也是非常重要的，因为在第三步我们虽然确定了迭代方向，并且知道这个方向是局部函数值下降最快的方向，但是还没有确定走的步长，如果选取的步长不合适，也是非常不可取的，下面会给出一个例子图，那么第四步的作用就是在确定迭代方向的前提上，确定在该方向上使得函数值最小的迭代步长。
下面给出迭代步长过大过小都不好的例子图：

从上图可以看出，选择一个合适的步长是非常最重要的，这直接决定我们的收敛速度。

四 最速梯度下降法实例

五 最速下降法的缺点

需要指出的是，某点的负梯度方向，通常只是在该点附近才具有这种最速下降的性质。
在一般情况下，当用最速下降法寻找极小点时，其搜索路径呈直角锯齿状（如下图），在开头 几步，目标函数下降较快；但在接近极小点时，收敛速度长久不理想了。特别适当目标函数的等值 线为比较扁平的椭圆时，收敛就更慢了。

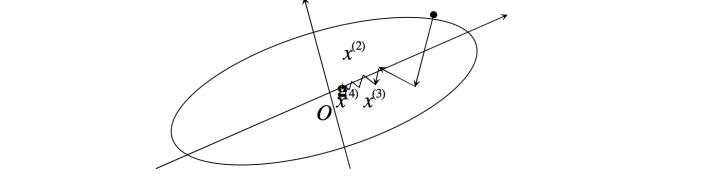
因此，在实用中常用最速下降法和其他方法联合应用，在前期使用最速下降法，而在接近极小值点时，可改用收敛较快的其他方法。

六 最速下降法与梯度下降法的区别

准确来说，它们并不是完全等价。
对于梯度下降法，我们需要预先设定步长α。

https://zhuanlan.zhihu.com/p/32709034