SFM（Structure from Motion）一点总结

运动结构恢复(Structure from motion)数十年来一直是计算机视觉领域的热门研究方向之一，实现了众多实际应用，尤其在近景三维重建中，该算法从获取的目标物系列影像出发，最终获取较高精度的目标物稀疏三维点云。

简介

运动结构恢复(Structure from motion)，即给出多幅图像及其图像特征的一个稀疏对应集合，估计3D点的位置，这个求解过程通常涉及3D几何（结构）和摄像机姿态（运动）的同时估计[1]。由于图像之间可能是无序的，并且图像数据量大，数据来源广而丰富。针对以上特点，出现了三种SFM策略包括增量式[2-12]、层级式[13]以及全局式[14-16]。关于三种策略示例图如图1，增量式即先选出两张影像进行初始化，接着一张张图像进行配准及点的三角化；全局式即一次性将所有的影像进行配准与重建；层级式先将影像进行分组，每组进行配准，再对上一步的结果进行配准重建。其中，增量式在无序图像数据集重建中应用最广泛，Bundler[17]、VisualSfM[18]、COLMAP[19]等优秀的SFM算法的出现，为SFM的应用与研究提供了基础。

SFM原理

以state-of-the-art的COLMAP算法为例，阐述一般SFM的原理流程，COLMAP算法流程（图2）

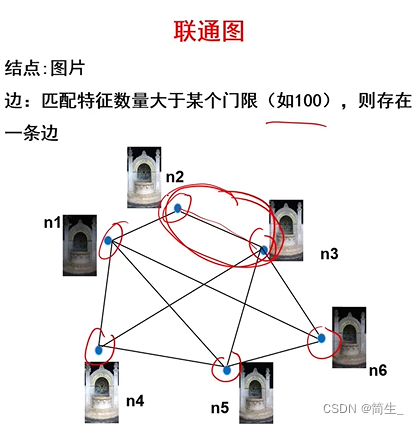
可以将上述多步总结为两个环节，一致性搜索及增量式重建。一致性搜索即找到数据集中有场景重叠的图像，识别出有场景重叠影像中同一个目标点在多张影像上的投影。一般采用SIFT算法进行特征点的提取，利用特征描述向量找到有场景重叠的影像，传统暴力方式测试每一对影像的重叠场景，对于一张影像中的每一个特征，根据特征向量找到另一张影像中最相似的特征，时间复杂度在大场景重建中是不允许的。因此，出现了很多改进方法包括MatchMiner[20]、Vocmatch[21]、PAIGE[22]等。一致性搜索的最后一步是精选上一步得到的可能有场景重叠的影像对，采用RANSAC[23]算法估计影像对之间的单应变换矩阵或者本质矩阵或者基础矩阵，判断是否有足够的特征匹配点满足映射关系，从而决定影像对是否真相关，最终获得场景图[4,10,20,24]，其中，影像为图节点，相关的图像对之间有边相连。
增量式重建阶段，输入前面得到的场景图，输出的是影像的姿态估计以及空间三维坐标点。初始化，选择场景图中有多相机视场角重叠的位置进行双目初始化，这样的初始化冗余度高，使得重建更加鲁棒和精确；影像配准，找到需配准影像中的已求解得到空间三维坐标的点，利用其2D和3D信息，通过RANSAC[18]及最小姿态解算器求解Perspective-n-Point问题[25]，获得新加进来的影像的位姿；三角化，即前方交会，新配准进来的影像，既能观测到已经存在的空间三维点，也能求解新的空间三维点，多视几何的三角化算法包括[26-33]；光束法平差，影像配准与三角化是一个相互联系的过程，配准的误差会影响三角化的准确性，反之亦然。随着配准及三角化过程的重复进行，累计误差越来越大，影响最终重建的结果。光束法平差[34]本质上是一个非线性优化算法，选取反向投影误差作为代价函数，该函数涉及待优化的相机内参、外参以及点云。过程中为了增加算法的鲁棒性，不受离群点的影响，增加Huber、Tukey等损失函数。求解BA问题包括严格方式[35、36]和不严格方式[37、38]，严格方式通过存储与分解为稀疏或密集矩阵优化参数，不严格方式通过一个迭代求解器，粗略估计参数。

国内外研究与应用

SFM技术针对大众数据（尤其针对城市建筑物）进行大尺度的三维建模，国内外出现了很多优秀的算法软件、以及相关的基准数据集；同时对SFM技术中的数据关联建立、光束法平差、多视立体视觉与融合等方面进行很多的研究。算法软件除了前面提及的增量式SFM的三个典型算法与软件外，在全局式SFM方面，出现了Theia[39]、OpenMVG[40]。在数据关联环节，除了COLMAP[19]提出的场景图方法外，还有[41]提出的Streaming Connected Component Discovery；在光束法平差环节出现了Ceres Solver[42]、PBA[43]、SSBA[44]等优秀的算法;在多视立体视觉与融合方面，除了COLMAP[19]算法外，还有CMVS/PMVS[45]、CMP-MVS[46]、Gipuma[47]、OpenMVS[48];在基准数据集方面，有高分辨率影像与多相机视频的多视立体视觉标准数据集[49]，提供的部分数据集见图3,Tanks and Temples标准数据集[50]，提供的部分数据集见图4。作为目前最优秀的SFM技术的COLMAP算法[19]，对传统SFM流程做了五点改进，分别是引入几何验证策略来标记场景图中的边的类型，以此提高初始化和三角化的鲁棒性；选择下一张最佳视图时充分考虑观测到的地图点数目和地图点均匀分布；一种计算成本更低，且鲁棒性更优的三角化方法；迭代BA，再三角化和异常值滤波策略能够减小累计误差，从而显著提高重建完整性和准确性；从无序图像集合挖掘相似视图，使之成组，从而减小BA计算量，提高BA准确性。在[51]中，对传统SFM流程做了三点改进：首先使用视觉索引用于影像对的选取，随机采样影像对，借助检测到的视觉单词评估场景重叠，计算tf-idf向量[52]评价相似度得分，缩短传统暴力匹配的计算时间；其次，应用图算法实现影像集压缩，采用快速多项式算法[53]计算图的近似最小支配集，从而选出可以代表输入影像集的子集，保证去除的影像在子集中至少可以找到一些有视觉重叠的影像；最后使用优先级队列分配重建的各个环节的顺序，借助优先顺序队列交叉进行影像连接与原子三维模型构建，可以保证在有限的时间内获得可靠的重建结果，每一个任务的优先权根据影像相似性集历史计算来设定。
在应用方面，[54]中介绍了利用Google Street View Pittsburgh Research Data Set进行大城市区域三维建模可视化；[55]中详细归纳了SFM技术的十类应用，包括增强现实、自主导航、运动捕捉、手眼标定、影像视频处理、基于影像的三维建模、遥感、图像组织与浏览、分割与识别、军事应用。以城市三维建模为例，获取复杂现实场景或目标物的精确真实三维模型的方式可粗略分为接触与非接触方式。非接触方式之一是基于影像的三维建模技术，因为SFM技术的广泛应用以及低成本，采用SFM三维建模是计算机视觉领域的研究热点。大到对以无人机为主要搭载平台所获取的大区域序列影像，恢复城市三维结构，小到对某一个建筑物，如利用老城区中古建筑文物的序列影像进行精细建模，结合现在的深度学习技术对古建筑中的裂缝等目标进行检测并提取，再根据SFM获取的影像姿态信息进行三维投影，可以定量地分析受损情况，便于下一步制定保护措施；甚至是网络上大量的无序相关影像，都可以利用SFM进行三维建模。图5展示了一个城市三维重建的结果。下一步针对SFM技术非实时性的问题，可以融合SLAM技术的实时性进一步优化。

SFM与摄影测量

作为计算机视觉领域的技术之一，SFM技术中的多个环节对应了传统摄影测量的多个环节。采用SIFT等特征提取算法进行特征点的提取与匹配是两者之间共有的，SFM中的极线约束在摄影测量里基于核线的影像匹配的思路一致，SFM中的三角化对应于摄影测量中的前方交会，SFM中的Bundle Adjustment正是摄影测量中的光束法平差的思路。所以SFM与传统摄影测量在三维重建方面异曲同工。同时也存在区别，SFM采用齐次坐标，且按照前文中PnP算法求解的外方位元素与传统摄影测量空三求解的外方位元素有所区别。转换过程如下：
背景：两个三维坐标系之间的变换有6个自由度：三个线元素和3个角元素，针对不同的应用可以采用不同的表达方式。由于计算机视觉界采用的外方位元素表达方式与摄影测量界惯用的表达方式不同，为了将COLMAP求解出来的外方位元素作为初值进行摄影测量光束法平差，需进行外方位元素间的变换。

针孔相机模型可以表示为：

两边同时乘以内参矩阵的逆，假设γ=0且fx=fy=f

展开左右两边即可得到针孔模型投影公式的等价形式：

摄影测量界常用的投影公式为：

计算机视觉界所采用的坐标系Z轴方向与摄影测量界相反且旋转角的定义也不同，上式进一步转换得到：

对比两个投影公式，即可得到外方位元素间的变换关系，转换后的外方位元素可以作为初值进行光束法平差：

在COLMAP中，求解出来的外方位元素形式为：四元数形式的旋转矩阵q（w,x,y,z）和平移矩阵（tx,ty,tz），转化为旋转矩阵形式，才可进一步求解：

上式带入上一页求解结果，可以得到最终转换关系：

参考文献

[1]: Szeliski R. Computer Vision: Algorithms and Applications[M]. Springer-Verlag New York, Inc. 2010
[2]: Agarwal S, Snavely N, SimonI, et al. Building Rome in a day[J]. Communications of the Acm, 2011,54(10):105-112.
[3]: Frahm J M, Fite-Georgel P,Gallup D, et al. Building Rome on a cloudless day[C]// European Conference on Computer Vision. Springer-Verlag, 2010:368-381.
[4]: Heinly J, Schönberger J L,Dunn E, et al. Reconstructing the world* in six days[C]// Computer Vision and Pattern Recognition. IEEE, 2015:3287-3295.
[5]: Schönberger J L, Frahm J M. Structure-from-Motion Revisited[C]// IEEE Conference on Computer Vision and Pattern Recognition. IEEE, 2016.
[6]: Wu C. Towards Linear-Time Incremental Structure from Motion[C]// International Conference on 3d Vision.IEEE Computer Society, 2013:127-134.
[7]: Snavely N,Seitz S M, Szeliski R. Modeling the World from Internet Photo Collections[J].
International Journal of Computer Vision, 2008, 80(2):189-210.
[8]: Snavely K N.Scene reconstruction and visualization from internet photo collections[M].
University of Washington, 2008.
[9]: Snavely N,Seitz S M, Szeliski R. Photo Tourism: Exploring Photo Collections In 3D[J]. Acm Transactions on Graphics, 2006, 25(3):págs. 835-846.
[10]: Snavely N,Seitz S M, Szeliski R. Skeletal graphs for efficient structure from motion[C]//Computer Vision and Pattern Recognition, 2008. CVPR 2008. IEEE Conference on.
IEEE, 2008:1-8.
[11]: Sweeney C,Fragoso V, Hollerer T, et al. Large Scale SfM with the Distributed Camera
Model[C]// Fourth International Conference on 3d Vision. IEEE, 2016:230-238.
[12]: Moulon P,Monasse P, Marlet R. Adaptive Structure from Motion with a Contrario Model Estimation[M]// Computer Vision – ACCV 2012. Springer Berlin Heidelberg,
2012:257-270.
[13]: R. Gherardi, M. Farenzena, and A. Fusiello.Improving the efficiency of hierarchical structure-and-motion[C]. CVPR,2010.
[14]: D. Crandall, A. Owens, N. Snavely, and D. P. Huttenlocher. Discrete-Continuous Optimizationfor Large-Scale Structure from Motion[C]. CVPR, 2011.
[15]: C. Sweeney, T. Sattler, T. Hollerer, M. Turk,and M. Pollefeys. Optimizing the viewing graph for structure-frommotion[C].CVPR, 2015.
[16]: K. Wilson and N. Snavely. Robust global translations with 1dsfm[C]. ECCV, 2014.
[17]: http://www.cs.cornell.edu/~snavely/bundler/
[18]: http://ccwu.me/vsfm/
[19]: https://colmap.github.io/
[20]: Y. Lou, N. Snavely, and J. Gehrke. MatchMiner: Efficient Spanning Structure
Mining in Large Image Collections[C]. ECCV, 2012.
[21]: M. Havlena and K. Schindler. Vocmatch: Efficient multiview correspondence for structure from motion[C]. ECCV, 2014.
[22]: J. L.Sch¨onberger, A. C. Berg, and J.-M. Frahm. PAIGE: PAirwise Image Geometry
Encoding for Improved Efficiency in Structure-from-Motion. CVPR, 2015.
[23]: M. A.Fischler and R. C. Bolles. Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography. ACM, 1981.
[24]: J. L. Sch¨onberger, A. C. Berg, and J.-M. Frahm. Efficient two-view geometry classification. GCPR, 2015.
[25]: Lepetit V, Moreno-Noguer F, Fua P. EPnP: An Accurate O(n) Solution to the PnP Problem[J]. International Journal of Computer Vision, 2009, 81(2):155-166.
[26]: Hartley R I, Sturm P. Triangulation[J]. Comput Vision Image Understanding, 1995,68(2):146-157.
[27]: Aholt C, Agarwal S, Thomas R. A QCQP Approach to Triangulation[M]// Computer Vision –ECCV 2012. Springer Berlin Heidelberg, 2012:654-667.
[28]: Hartley R , Schaffalitzky F . L-∞Minimization in Geometric Reconstruction Problems[C]// IEEE Computer Society Conference on Computer Vision & Pattern Recognition. IEEE, 2004.
[29]: H. Li. A practical algorithm for L∞ triangulation with outliers[C]. CVPR, 2007.
[30]: Lu F ,Hartley R . A Fast Optimal Algorithm for L2 Triangulation[C]// Asian Conference
on Computer Vision. Springer-Verlag, 2007.
[31]: Agarwal S ,Snavely N , Seitz S M . Fast algorithms for L∞problems in multiview geometry[C]// IEEE Conference on Computer Vision & Pattern Recognition. IEEE, 2008.
[32]: Olsson C,Eriksson A, Hartley R. Outlier removal using duality[C]// Computer Vision and Pattern Recognition. IEEE, 2010:1450-1457.
[33]: Kang L ,Lingda W U , YANG, et al. Robust multi-view L2 triangulation via optimal inlier
selection and 3D structure refinement[J]. Pattern Recognition, 2014,47(9):2974-2992.
[34]: Triggs B ,Zisserman A , Szeliski R . [Lecture Notes in Computer Science] Vision Algorithms: Theory and Practice Volume 1883 || Bundle Adjustment — A Modern Synthesis[J]. VisionAlgorithms Theory & Practice, 2000, 10.1007/3-540-44480-7(Chapter 21):298-372.
[35]: Chen Y , Chen Y , Davis T A , et al. Algorithm 887: CHOLMOD, supernodal sparse Cholesky factorization and update/downdate[J]. Acm Transactions on Mathematical
Software, 2008, 35(3):1-14.
[36]: Lourakis M I A . SBA : A software package for generic sparse bundle adjustment[J]. AcmTrans.math.softw, 2009, 36(1):2.
[37]: Agarwal S ,Snavely N , Seitz S M , et al. Bundle Adjustment in the Large[J]. 2010.
[38]: Wu C, Agarwal S, Curless B, et al. Multicore bundle adjustment[C]// Computer Vision and Pattern Recognition. IEEE, 2011:3057-3064.
[39]: http://www.theia-sfm.org/
[40]: https://github.com/openMVG/openMVG
[41]: https://github.com/jheinly/streaming_connected_component_discovery
[42]: http://ceres-solver.org/
[43]: https://grail.cs.washington.edu/projects/mcba/
[44]: https://github.com/chzach/SSBA
[45]: https://www.di.ens.fr/cmvs https://www.di.ens.fr/pmvs
[46]: http://ptak.felk.cvut.cz/sfmservice/websfm.pl?menu=cmpmvs
[47]: https://hithub.com/kysucix/gipuma
[48]: https://github.com/cdcseacave/openmvs
[49]: https://www.eth3d.net/datasets
[50]: A. Knapitsch, J. Park, Q. Zhou, V. Koltun. SIGGRAPH 2017. https://www.tanksandtemples.org/
[51]: Michal Havlena. Incremental Structure from Motion for Large Ordered and Unordered Sets of Images[D]. Czech Technical University,2012.
[52]: Sivic J ,Zisserman A . Video Google: Efficient Visual Search of Videos[J]. Lncs, 2006,
4170:127-144.
[53]: Guha S ,Khuller S . Approximation Algorithms for Connected Dominating Sets[J]. Algorithmica,1998, 20(4):374-387.
[54]: Torii A ,Havlena M , Tomás Pajdla.Omnidirectional Image Stabilization by Computing Camera Trajectory[C]//Advances in Image and Video Technology, Third Pacific Rim Symposium, PSIVT 2009, Tokyo, Japan, January 13-16, 2009. Proceedings. Springer Berlin
Heidelberg, 2009.
[55]:Ying-meiWEI, LaiKANG, BingYANG, et al. Applications of structure from motion : a survey[J]. 信息与电子工程前沿 (英文),2013(7).