引入

$$N=S\times r^j$$

• N：浮点数
• S：尾数
• r：基数
• j：阶码

举个例子：
$$123.456=1.23456\times 10^2$$
其中123.456是浮点数，1.23456是尾数，10是基数(10进制)，2是阶码。

可以发现，表示123.456的方法不唯一，比如：
$$123.456=12.3456\times 10^1=0.123456\times 10^3=0.0123456\times 10^4=...$$

---

在二进制中也是如此：

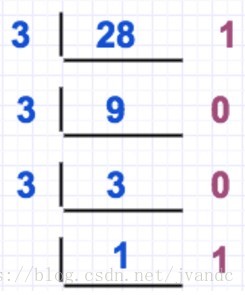
10进制转化为二进制
$$11.625_{10}=1011.101_2$$

表示方法同样多种：
$$1011.101=0.1011101\times 2^{100}=1.011101\times 2^{11}=...$$
指数部分也用二进制表示，2¹⁰⁰表示2⁴，2¹¹表示2³

可以看出，表示一个数的方式太多，因此要有一个规范(IEEE 754)，在讲规范之前，先了解一下基础概念。

定点数

计算机中是没有通过硬件来表示小数点的，因此小数点及其位置是隐含规定的，所谓定点就是小数点的位置不变。

定点数又分为定点整数和定点小数。

定点整数

小数点隐含在最低位之后，最高位为符号位。

• 为什么有符号位？

  计算机中用补码表示数(补码不会有+0和-0之分)，补码的最高位为符号位。

举个例子：
$$-13_{10}=-1101_2$$
用8位的定点整数来表示10进制的-13：

如果是13，则将符号位改为0

• 为什么符号位0表示正，1表示负？

  数的符号表示为：-1^符号位

  • 若符号位=0，则数的符号为-1⁰ = 1,表示正数
  • 若符号位=1，则数的符号为-1¹ = -1，表示负数

定点小数

小数点隐含与数值位与符号位之间

举个例子：
$$0.625_{10}=0.101_2$$
若用8位的定点小数来表示10进制的0.625：

然而生活中的数常常不是纯整数或是纯小数，而是两者的结合

IEEE 754规范

因为表示一个浮点数的方法有很多，但是计算机中要有一个统一的规范，这规范就是IEEE 754

本文讲IEEE 754的Float32标准
$$V=-1^S\times M\times R^E$$
V：浮点数

R：基数

• 符号：1bit
• 指数：8bit
• 尾数：23bit

同时规定：

• $$1\le M＜2$$

  因此尾数的第一位固定为1，并且在表示时忽略。

• 尾数M采用的是定点小数表示。

• E为无符号整数，但因为指数可以为负数，因此IEEE 754规定E要减去127(这个127有个高大上的名字：偏置)

  指数有8bit并且是无符号整数，所以E∈[0, 255]

  而减去127后，E∈[-127, 128]

• 指数E采用的是定点整数表示。

• 用符号位来表示尾数的符号

示例1

$$-9.625_{10}=-1001.101_2$$

尾数M = 1.001101

指数E = 3₁₀ = 11₂

• 上面提到过，尾数小数点左侧的1忽略，因此尾数表示为：

• 指数在表示时会减去127，因此指数部分的实际值应该为:
  $$127+3=130_{10}=10000010_2$$
  指数表示为：

  

• -9.625为负数，因此符号位=1(-1¹=-1)，符号位表示为：

  

-9.625表示为：

示例2

$$0.09375_{10}=0.00011_2$$

$$2^{-4}=0.0625,2^{-5}=0.03125,2^{-4}+2^{-5}=0.09375$$

• 尾数M = 1.1

  尾数的小数点左侧的1忽略，所以M表示为：

  

• 指数E = -4

  因为要减去127这个偏置，所以E=123(123-127=-4)，二进制为：01111011，所以E表示为：

  

• 符号S = 0

  因为0.09375为正数，符号为-1⁰ = 1，符号位表示为：

  

0.09375表示为：