数据拟合丨人口预测模型

路漫漫其修远兮，吾将上下而求索

  下表所列是某地区1971一2000年的人口数据，试给出该地区人口增长的数学模型。

年 份	时间变量 $t$=年份-1970	人口 $y$/人	年 份	时间变量 $t$=年份-1970	人口 $y$/人
1971	1	33815	1986	16	34520
1972	2	33981	1987	17	34507
1973	3	34004	1988	18	34509
1974	4	34165	1989	19	34521
1975	5	34212	1990	20	34513
1976	6	34217	1991	21	34515
1977	7	34344	1992	22	34517
1978	8	34458	1993	23	34519
1979	9	34498	1994	24	34519
1980	10	34476	1995	25	34521
1981	11	34483	1996	26	34521
1982	12	34488	1997	27	34523
1983	13	34513	1998	28	34525
1984	14	34497	1999	29	34525
1985	15	34511	2000	30	34527

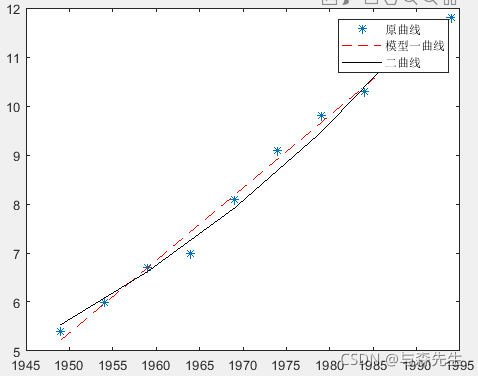
  根据表中的数据，做出散点图，如图所示。
  由图可以看出，人口随时间的变化呈非线性变化，而且存在一个与横坐标轴平行的渐近线，故可以用Logistic曲线模型进行拟合。

  因为Logistic曲线模型的基本形式为

$$y=\frac{1}{a+be^{-t}}$$
  所以，只要令 $y'=\frac{1}{y}，x’=e^{-t}$，就可以将其转化为直线模型
$$y'=a+bx'$$
   下面，用MATLAB进行回归分析拟合计算。回归拟合程序如下：

clear
clc
% 读入人口数据（1971－2000年）
Y=[33815    33981   34004   34165   34212   34327   34344   34458   34498   34476   34483   34488   34513   34497   34511   34520   34507   34509   34521   34513   34515   34517   34519   34519   34521   34521   34523   34525   34525   34527]
% 读入时间变量数据（t＝年份－1970）
T=[1    2   3   4   5   6   7   8   9   10  11  12  13  14  15  16  17  18  19  20  21  22  23  24  25  26  27  28  29  30]
% 线性化处理
for t=1:30x(t)=exp(-t);y(t)=1/Y(t);
end
% 计算，并输出回归系数B,即计算回归方程 y'=a+bx' 中的a和b的值
c=zeros(30,1)+1;
X=[c,x'];%相当于30个方程组，求解a和b 的值.
B=inv(X'*X)*X'*y'
for i=1:30,
% 计算回归拟合值    z(i)=B(1,1)+B(2,1)*x(i);
% 计算离差s(i)=y(i)-sum(y)/30;
% 计算误差    w(i)=z(i)-y(i);
end
% 计算离差平方和S
S=s*s';
% 回归误差平方和Q
Q=w*w';
% 计算回归平方和U
U=S-Q;
% 计算，并输出F检验值
F=28*U/Q
% 计算非线性回归模型的拟合值
for j=1:30,Y(j)=1/(B(1,1)+B(2,1)*exp(-j));
end
% 输出非线性回归模型的拟合曲线（Logisic曲线）
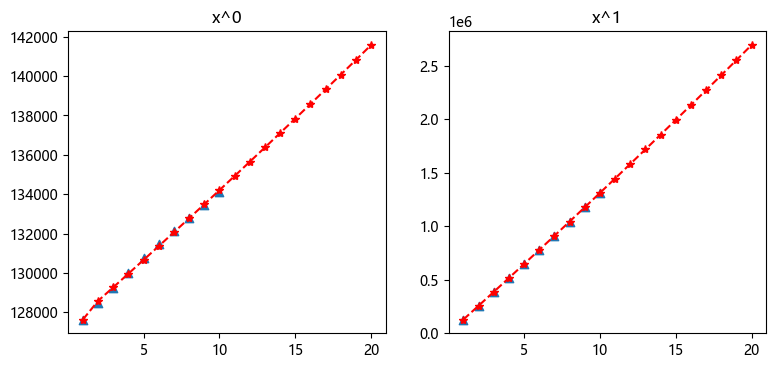
plot(T,Y,'r*')

  运行结果：

  当数据较多时，从Excel中读取数据：

clear
clc
Y=xlsread('D:\file.xlsx',1,'B1:B30');%读取数据
Y=Y';
T=xlsread('D:\file.xlsx',1,'A1:A30');%读取数据
T=T';
for t=1:30,x(t)=exp(-t);y(t)=1/Y(t);
end
c=zeros(30,1)+1;
X=[c,x'];
B=inv(X'*X)*X'*y'%B=inv(X'*X)*X'*y'for i=1:30,z(i)=B(1,1)+B(2,1)*x(i);s(i)=y(i)-sum(y)/30;w(i)=z(i)-y(i);
end
S=s*s';
Q=w*w';
U=S-Q;
F=28*U/Q
for j=1:30,Y(j)=1/(B(1,1)+B(2,1)*exp(-j));
end
plot(T,Y)

  运行结果：