预测人口模型

利用灰色预测模型预测人口

应用

灰色预测模型（Gray Forecast Model）是通过少量的、不完全的信息，建立数学模型并做出预测的一种预测方法。是处理小样本（4个就可以）预测问题的有效工具，而对于小样本预测问题回归和神经网络的效果都不太理想。

灰色系统

我们称信息完全未确定的系统为黑色系统，称信息完全确定的系统为白色系统，灰色系统就是这介于这之间，一部分信息是已知的，另一部分信息是未知的，系统内各因素间有不确定的关系。

特点

用灰色数学处理不确定量，使之量化。
充分利用已知信息寻求系统的运动规律。
灰色系统理论能处理贫信息系统。

灰色生成数列

灰色系统理论认为，尽管客观表象复杂，但总是有整体功能的，因此必然蕴含某种内在规律。关键在于如何选择适当的方式去挖掘和利用它。灰色系统时通过对原始数据的整理来寻求其变化规律的，这是一种就数据寻求数据的现实规律的途径，也就是灰色序列的生产。一切灰色序列都能通过某种生成弱化其随机性，显现其规律性。数据生成的常用方式有累加生成、累减生成和加权累加生成。常用的是累加生成。
设原始数据为设原始数据为 $x^{(0)}=\left(x^{0}(1), x^{0}(2), \ldots \ldots, x^{0}(n)\right)$

1.累加生成

$x^{1}(1)=x^{0}(1)$

$x^{1}(2)=x^{0}(1)+x^{0}(2)$

$x^{1}(3)=x^{0}(1)+x^{0}(2)+x^{0}(3)$

$x^{1}(n)=x^{0}(1)+x^{0}(2)+\ldots \ldots+x^{0}(n)$

累加的数据为 $x^{(1)}=\left(x^{1}(1), x^{1}(2), \ldots \ldots, x^{1}(n)\right)$
例如有一组数据的的折线如下
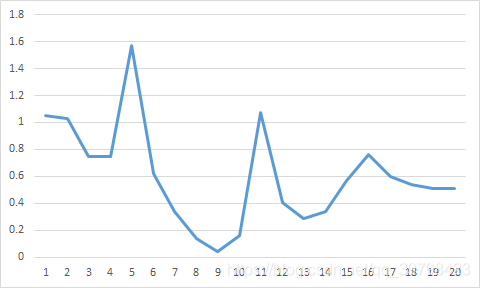
在这里插入图片描述
此时不能看出数据有什么的规律，但经过累加生成后的结果如下

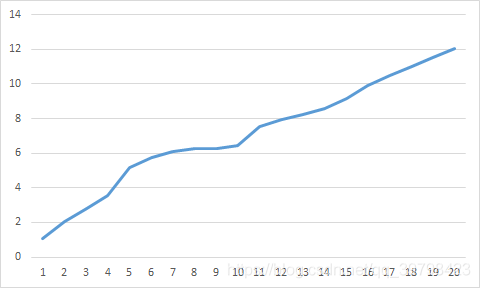
看起来就是一个递增的规律（这是20期某大坝变形位移的数据，顺水流方向的形变一定都是正的)

2.加权临值生成

$z^{0}(2)=a x^{0}(2)+(1-a) x^{0}(1)$
$z^{0}(3)=a x^{0}(3)+(1-a) x^{0}(2)$
$z^{0}(4)=a x^{0}(4)+(1-a) x^{0}(3)$
$\ldots$
$z^{1}(n)=a x^{0}(n)+(1-a) x^{0}(n-1)$

由此得到的数列称为邻值生成数，权 $\alpha$ 也称为生成系数。特别地，当生成系数 $\alpha=$ $0.5$ 时，则称该数列为均值生成数，也称为等权邻值生成数。

灰色模型GM(1,1)

GM代表grey model（灰色模型），GM(1,1)是一阶微分方程模型。

1.数据检验

使用 $\mathrm{GM}(1,1)$ 建模需要对数据进行检验，首先计算数列的级比

$\lambda(k)=\frac{x^{0}(k-1)}{x^{0}(k)}$ , 其中 $\ldots, n$

如果所有的级比都落在可容覆盖区间 $X=\left(e^{\frac{-2}{n+1}}, e^{\frac{2}{n+1}}\right)$ 内，则数列 $\left.x^{(} 0\right)$ 可以建立

$\mathrm{GM}(1,1)$ 模型进行灰色预测。否则就需要对数据做适当的变换处理，如平移等。

2.构建灰色模型

定义 $x^{(1)}$ 的灰导数为

$d(k)=x^{0}(k)=x^{1}(k)-x^{1}(k-1)$

令 $z^{1}(k)$ 为数列 $x^{1}$ 的邻值生成数列，即

$z^{1}(k)=a x^{1}(k)+(1-a) x^{1}(k-1)$

于是定义 $G M (1, 1)$ 的灰微分方程模型为

$d(k)+a z^{1}(k)=b$

其中， $a$ 称为发展系数， $z^{1}(k)$ 称为白化背景值， $b$ 称为灰作用量。接下来我们得到如下方程组

$x^{0}(2)+a z^{1}(2)=b$

$x^{0}(3)+a z^{1}(3)=b$

$x^{0}(n)+a z^{1}(n)=b$

按照矩阵的方法列出

$
u=\left[\begin{array}{l}
a \
b
\end{array}\right], Y=\left[\begin{array}{c}
x^{0}(2) \
x^{0}(3) \
\ldots \
x^{0}(n)
\end{array}\right], B=\left[\begin{array}{cc}
-z^{1}(2) & 1 \
-z^{1}(3) & 1 \
\cdots & \
-z^{1}(n) & 1
\end{array}\right]
$

则 $\mathrm{GM}(1,1)$ 就可以表示为 $Y = B u$ ，接下来就是求 $a$ 和 $b$ 的值，可以使用线性回归或者 $\left(B^{T} B\right)^{-1} B^{T} Y$ (正规方程) 等按眧最小二乘的原埋来求出 $a$ 和 $b$ 的值 (这里在列方程时 $a$ 可以随便写一个数，比如 $\frac{1}{2}$ ，这样 $a$ 和 $(1 - a)$ 就一样的可以提出来方便写) 。

3.预测

相应的白化模型为

$\frac{d x^{1}(t)}{d t}+a x^{1}(t)=b$

由此得到 $x^{1}(t)$ 的解为

$x^{1}(t)=\left(x^{0}(1)-\frac{b}{a}\right) e^{-a(t-1)}+\frac{b}{a}$

令 $t + 1 = t$ 有

$x^{1}(t+1)=\left(x^{0}(1)-\frac{b}{a}\right) e^{-a}+\frac{b}{a}$ , 其中 $\ldots, n-1$

这就是我们的预测值。

4.检验

灰色模型的精度检验一般有三种方法灰色模型的精度检验一般有三种方法，相对误差大小检验法，关联度检验法和后验差检验法。常用的为后验差检验法。

将预测的 $\hat{x}^{1}$ 使用累减生成得到

$\hat{x}^{0}$ $\hat{x}^{0}(k)=\hat{x}^{1}(k)-\hat{x}^{1}(k-1)$ , 其中 $\ldots, n$
计算残差
$e(k)=x^{0}(k)-\hat{x}^{0}(k)$ , 其中 $\ldots, n$
计算原始序列 $x^{0}$ 的方差 $S_{1}$ 和残差 $e$ 的方差 $S_{2}$
$S_{1}=\frac{1}{n} \sum_{k=1}^{n}\left(x^{0}(k)-\bar{x}\right)^{2}$ $S_{2}=\frac{1}{n} \sum_{k=1}^{n}(e(k)-\bar{e})^{2}$
计算后验差比
$C=\frac{S_{2}}{S_{1}}$
查表观察效果

模型精度等级	均方差比值C
1 级(好)	C<=0.35
2 级（合格）	C<=0.5&c>0.35
3 级（勉强）	C<=0.65&c>0.5
4 级（不合格）	C>0.65

灰色预测模型预测人口

1.输入数据

从国家统计局获取十年的人口数据

人口数据	年份
127627	2011
128453	2012
129227	2013
129988	2014
130756	2015
131448	2016
132129	2017
132802	2018
133450	2019
134091	2020

采用灰色预测模型预估的后十年的人口数据

人口数据（万人）	年份	预测数据(万人)	误差率
127627	2001	127627	0.000%
128453	2002	128575.416	0.095%
129227	2003	129265.6577	0.030%
129988	2004	129959.6049	0.022%
130756	2005	130657.2774	0.076%
131448	2006	131358.6954	0.068%
132129	2007	132063.8788	0.049%
132802	2008	132772.8479	0.022%
133450	2009	133485.623	0.027%
134091	2010	134202.2245	0.083%
134916	2011	134922.6731	0.005%
135922	2012	135646.9893	0.202%
136726	2013	136375.1939	0.257%
137646	2014	137107.3077	0.391%
138326	2015	137843.3519	0.349%
139232	2016	138583.3474	0.466%
140011	2017	139327.3155	0.488%
140541	2018	140075.2774	0.331%
141008	2019	140827.2548	0.128%
141212	2020	141583.269	0.263%

误差率均在1%以下，效果很好。

以2011-2020年数据预测未来十年的人口数据

年份	人口数目（万人）
2021	142440.9
2022	143150.2
2023	143863.1
2024	144579.5
2025	145299.5
2026	146023
2027	146750.2
2028	147481
2029	148215.5
2030	148953.6

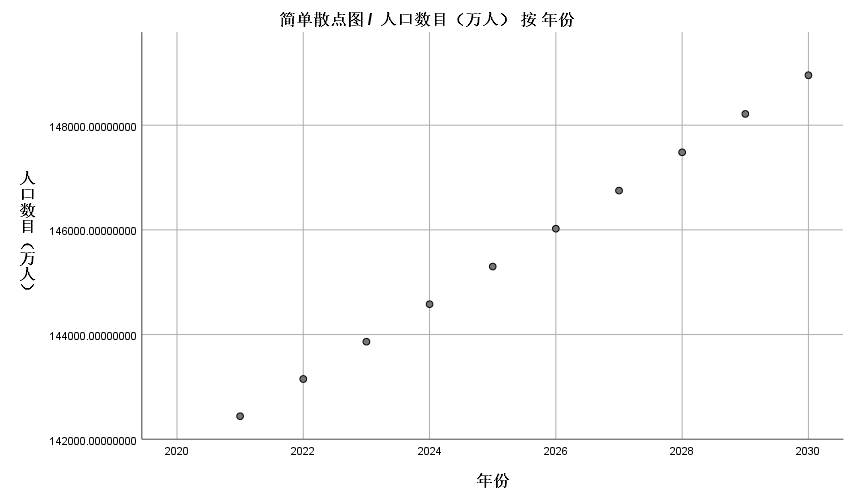
近似为一条直线，但根据国家统计局预测，我国人口将在10年内迎来拐点。

故更换预测模型。

按自然增长率预测

自然增长率数据

年份	自然增长率
2011	6.13
2012	7.43
2013	5.9
2014	6.71
2015	4.93
2016	6.53
2017	5.58
2018	3.78
2019	3.32
2020	1.45

绘制自然增长率散点图

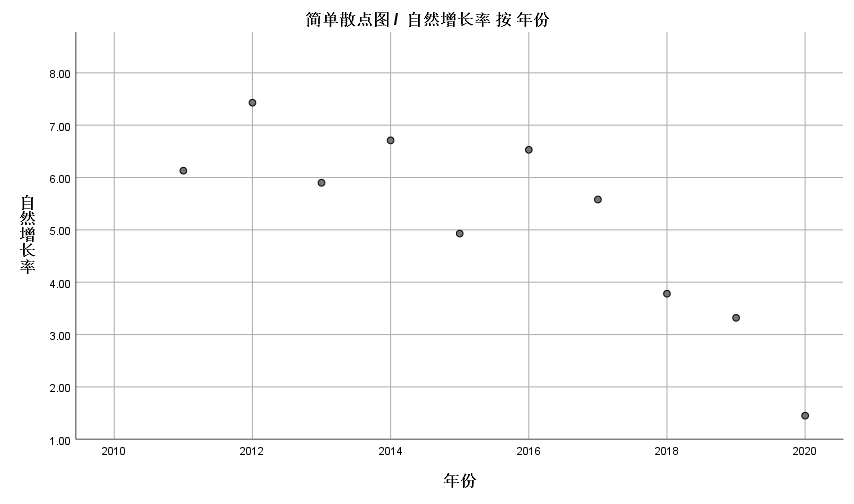
散点图没有呈现适合灰度模型的性质（指数型），且波动较大，尝试运用灰度模型，部分输出为（舍去了预测数据）

该数据未通过检验
a=[0.10967811]
b=[8.69394742]2级，效果合格

数据未经过检验，故不采用灰度模型预测自然生产率。

运用SPSS对自然增长率进行曲线估算分析

运用曲线估算分析，分析哪种模型适合对人口进行预测。

曲线估算分析结果如下：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-kSJ9iqM6-1639318859800)(https://s2.loli.net/2021/12/12/YcnwZG7IEJ1OzVd.png)]

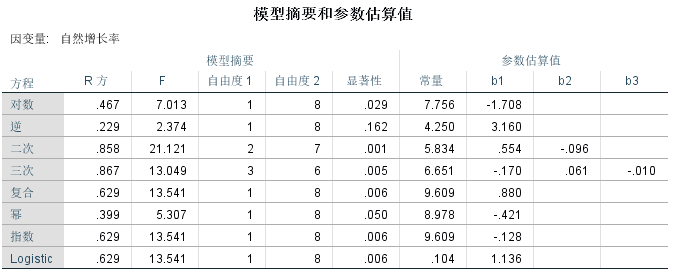
其对数、二次、三次、复合、幂、指数函数的拟合显著性都低于0.05，均可采用，且二次函数最可信。

此处选择二次函数，所得未来5年的自然增长率如下：

年份	自然增长率（‰）
2021	0.202
2022	-1.462
2023	-3.318
2024	-5.366
2025	-7.606

根据自然增长率预估未来5年人口

年份	人口及预测人口（万人）
2021	141240.5
2022	141034
2023	140566.1
2024	139811.8
2025	138748.4

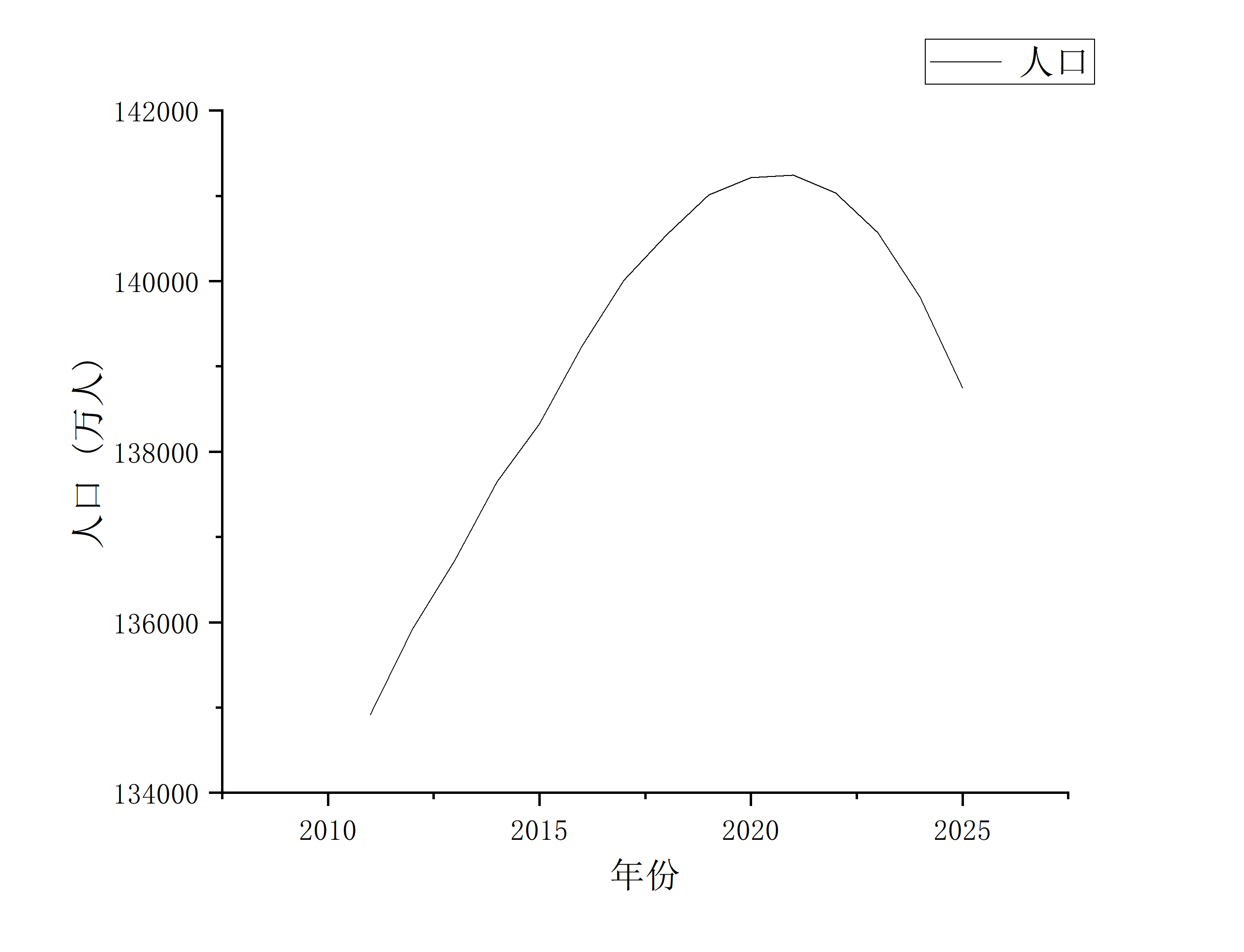
人口转折点在2022年。

灰色预测模型python代码

# 灰色模型预测import numpy as np
import pandas as pd
import matplotlib.pyplot as pltdir = 'C:\\Users\\shuai\\Desktop\\工程统计学\\讨论课'data = pd.read_csv(dir+'\\test.csv')
data = np.array(data['pdata'])
lens = len(data)  # 数据量# 数据检验
## 计算级比
lambds = []
for i in range(1, lens):lambds.append(data[i-1]/data[i])
## 计算区间
X_min = np.e**(-2/(lens+1))
X_max = np.e**(2/(lens+1))
## 检验
is_ok = True
for lambd in lambds:if (lambd < X_min or lambd > X_max):is_ok = False
if (is_ok == False):print('该数据未通过检验')
else:print('该数据通过检验')# 构建灰色模型GM(1,1)
## 累加数列
data_1 = []
data_1.append(data[0])
for i in range(1, lens):data_1.append(data_1[i-1]+data[i])
## 灰导数及临值生成数列
ds = []
zs = []
for i in range(1, lens):ds.append(data[i])zs.append(-1/2*(data_1[i-1]+data_1[i]))
## 求a、b
B = np.array(zs).reshape(lens-1,1)
one = np.ones(lens-1)
B = np.c_[B, one]  # 加上一列1
Y = np.array(ds).reshape(lens-1,1)
a, b = np.dot(np.dot(np.linalg.inv(np.dot(B.T, B)), B.T), Y)
print('a='+str(a))
print('b='+str(b))# 预测
def func(k):c = b/areturn (data[0]-c)*(np.e**(-a*k))+c
data_1_hat = []  # 累加预测值
data_0_hat = []  # 原始预测值
data_1_hat.append(func(0))
data_0_hat.append(data_1_hat[0])
for i in range(1, lens+10):  # 多预测10次data_1_hat.append(func(i))data_0_hat.append(data_1_hat[i]-data_1_hat[i-1])
print('预测值为：')
for i in data_0_hat:print(i)# 模型检验
## 预测结果方差
data_h = np.array(data_0_hat[0:10]).T
sum_h = data_h.sum()
mean_h = sum_h/lens
S1 = np.sum((data_h-mean_h)**2)/lens
## 残差方差
e = data - data_h
sum_e = e.sum()
mean_e = sum_e/lens
S2 = np.sum((e-mean_e)**2)/lens
## 后验差比
C = S2/S1
## 结果
if (C <= 0.35):print('1级，效果好')
elif (C <= 0.5 and C >= 0.35):print('2级，效果合格')
elif (C <= 0.65 and C >= 0.5):print('3级，效果勉强')
else:print('4级，效果不合格')# 画图
plt.figure(figsize=(9, 4), dpi=100)
x1 = np.linspace(1, 10, 10)
x2 = np.linspace(1, 20, 20)
plt.subplot(121)
plt.title('x^0')
plt.plot(x2, data_0_hat, 'r--', marker='*')
plt.scatter(x1, data, marker='^')
plt.subplot(122)
plt.title('x^1')
plt.plot(x2, data_1_hat, 'r--', marker='*')
plt.scatter(x1, data_1, marker='^')
plt.show()

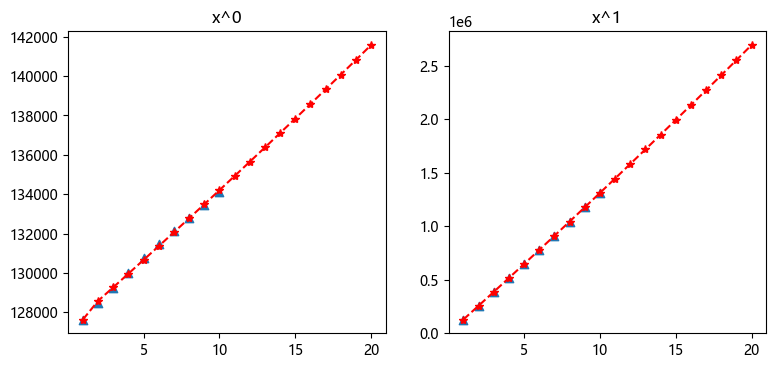
输出结果如下

该数据通过检验
a=[-0.00535402]
b=[127548.20761512]
预测值为：
[127627.]
[128575.41598519]
[129265.6576876]
[129959.60486981]
[130657.27742425]
[131358.69535014]
[132063.87875406]
[132772.84785051]
[133485.62296254]
[134202.22452229]
[134922.67307159]
[135646.98926251]
[136375.19385806]
[137107.30773265]
[137843.35187279]
[138583.34737763]
[139327.31545959]
[140075.277445]
[140827.25477463]
[141583.26900437]
1级，效果好