一、辗转相除法
辗转相除法又称为欧几里得算法,用于求两数的最大公约数gcd(全称为greatest common divisor)
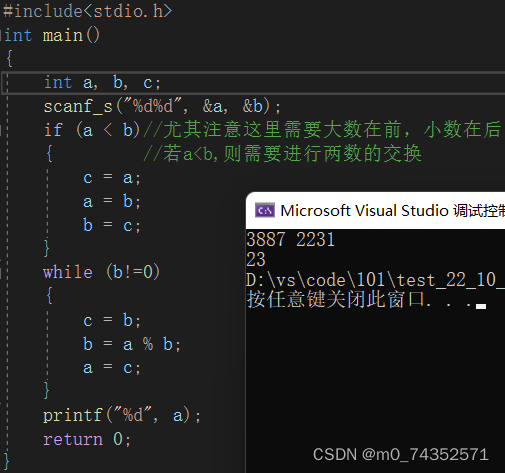
注意两数必须为非负整数a,b。用法为:用两数中较大的数(a1)除以较小的数(b1),得到余数(r1),再用b1除以r1得到余数r2,之后再用r1除以r2,反复进行,直到最后余数是0为止。最大公约数就是最后式子中的除数。请看如下举例:

若用函数gcd(a,b)来表示,即gcd(a,b)=gcd(b,a%b),我们可以这样理解:3887 2231和2231 1656的最大公约数是相等的,依次类推、重复操作。用表达式可以这样来表示:gcd(3887,2231)=gcd(2231,1656)=gcd(1656,575),直到最后到底gcd(a,b)=gcd(c,0),即gcd(3887,2231)=gcd(23,0)。这里的c为a和b的最大公约数。
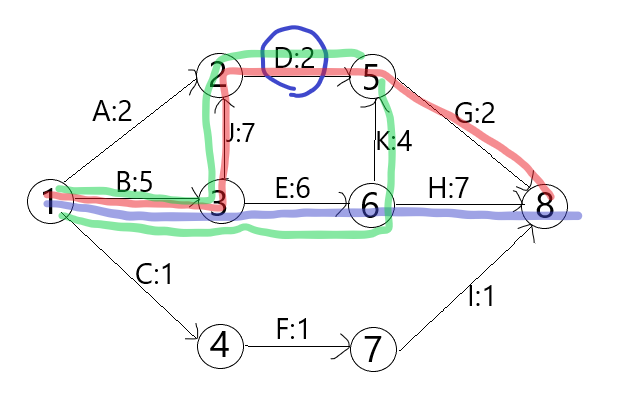
下面来看辗转相除法的图像说明
下面看算法实现:
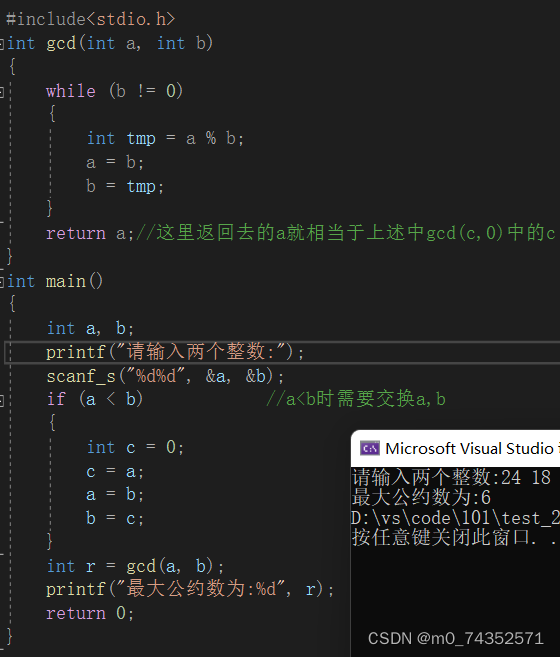
算法实现一
代码中的a就相当于上述gcd(a,b)=gcd(c,0)中的c。当然还有利用此原理的其他写法,不过是大同小异,这里就不一一列举了。这里的if语句其实是多余的,因为通过辗转相除完全可以实现两数之间的互换。
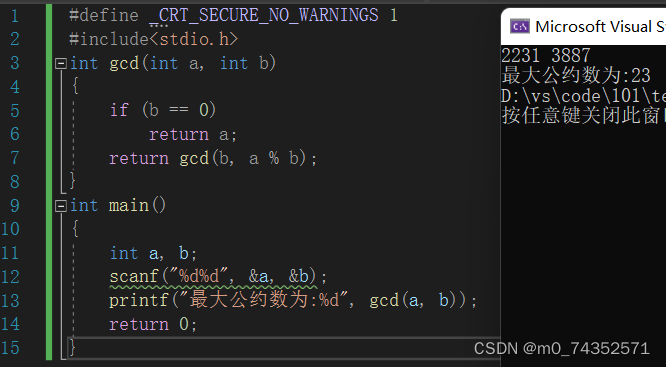
算法实现二(函数递归法)
对辗转相除足够熟悉后,可以采用递归的方式,如算法实现三
算法实现三(递归思想)
总之一句话:除数除以余数,直到余数为0为止。
二、更相减损之术
更相减损之术出自我国《九章算术》,原文是这样的:
可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也。以等数约之。
算法过程:大数减小数,得到的差用来替换之前的大数,如此反复,直到得出来的差与上次的减数相等。此时的这个差就是两者的最大公约数。
以 36 24为例(如下图):

可以这样表示:gcd(36,24)=gcd(24,12),即36 24和24 12的最大公约数是相等的。
下面来看代码实现
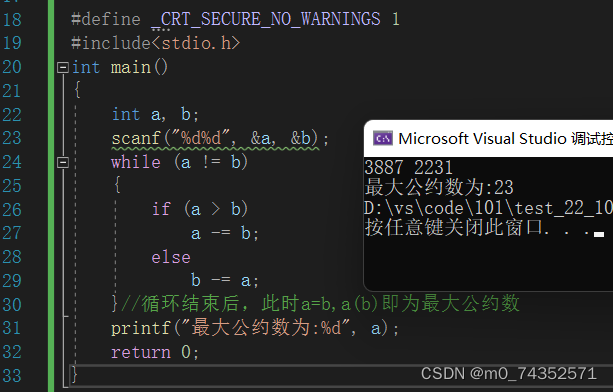
总归一句话:用大数减去小数,知道减数和差相等。
最后,当处理较大的数时,辗转相除法虽然在时间上有明显优势。但是,即使是这样,辗转相除法也同样存在缺陷,其在处理较大的素因数(也叫质因数,就是说一个数是另一个数的因数,本身又是质数,就叫做另一个数的素因数)时,缺陷就会显现出来。
当然,实现求取最大公约数还有很多其他方法,这里只进行了常见思路的讲解。