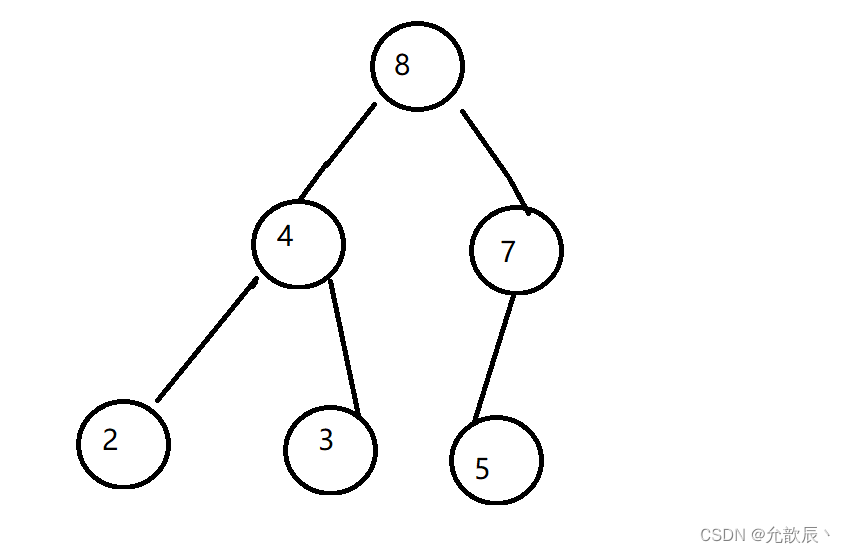
完全二叉树：叶子结点只能出现在最下层和次下层，且最下层的叶子结点集中在树的左部。即除了最后一层，其他层的节点个数都是满的，而且最后一层的叶子节点必须靠左。

如图：

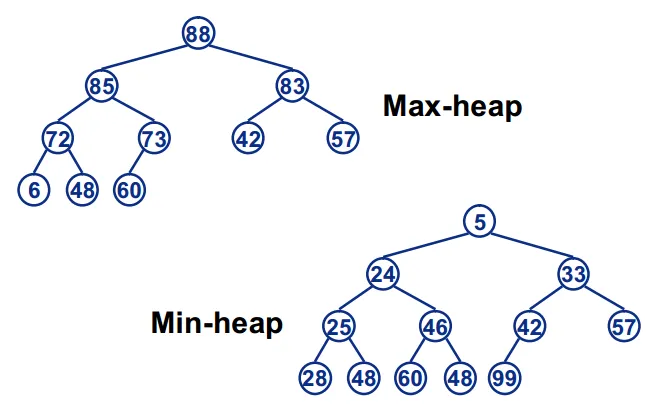
二叉堆：必须是完全二叉树，二叉堆中的每一个节点，都必须大于等于（或小于等于）其子树中每个节点的值。若是每个节点大于等于子树中的每个节点，我们称之为大顶堆，小于等于子树中的每个节点，我们则称之为小顶堆。

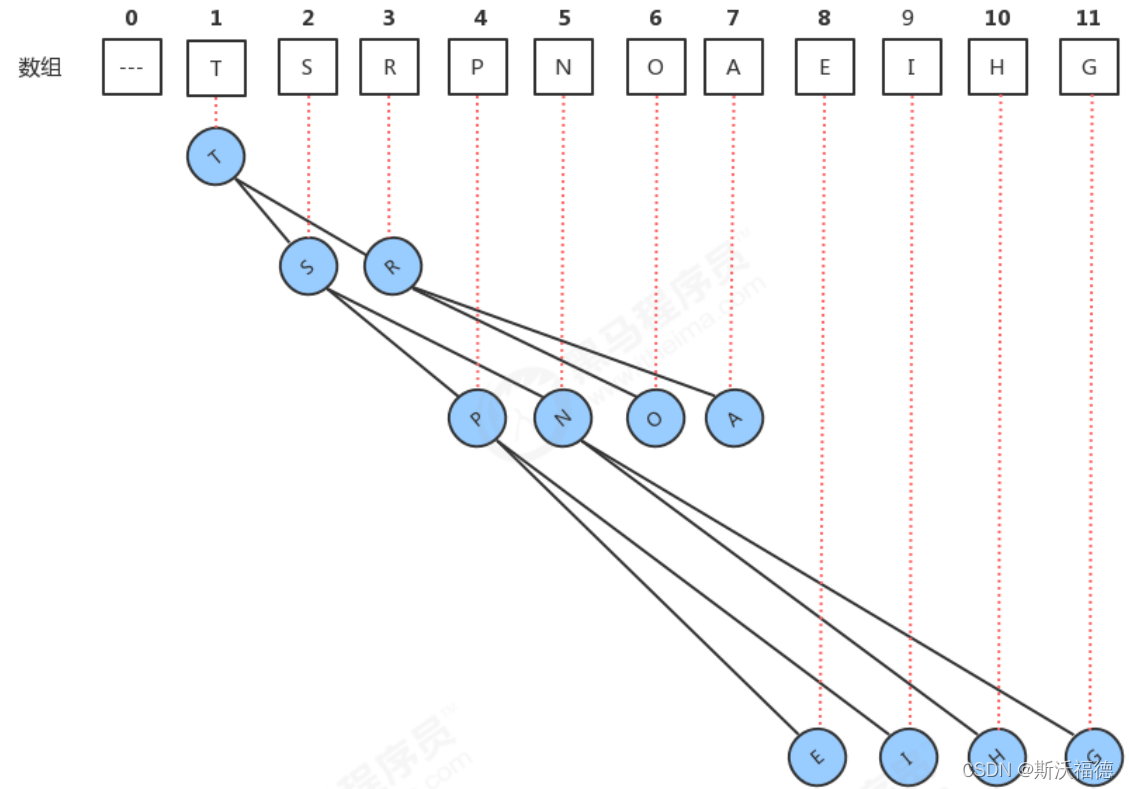
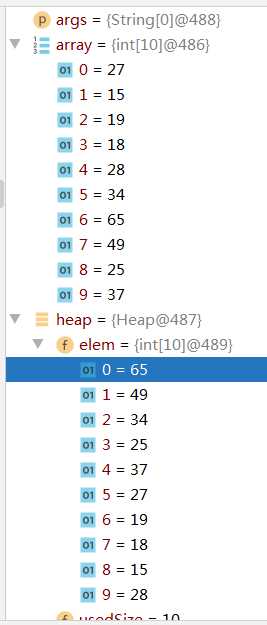
对于java中的堆，我们使用数组来实现

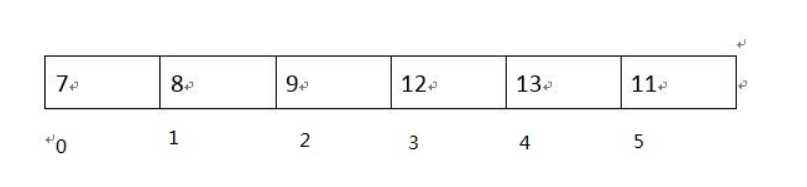
可以看出，通过一个节点在数组中的索引计算出它的父节点及左右孩子节点的索引。

//返回左节点
public int left(int i) {return (i + 1) * 2 - 1;
}
//返回右节点
public int right(int i) {return (i + 1) * 2;
}
//返回根节点
public int parent(int i) {// i为根结点if (i == 0) {return -1;}return (i - 1) / 2;
}

堆排序其实主要有两个步骤：建堆和排序

1. 建堆：

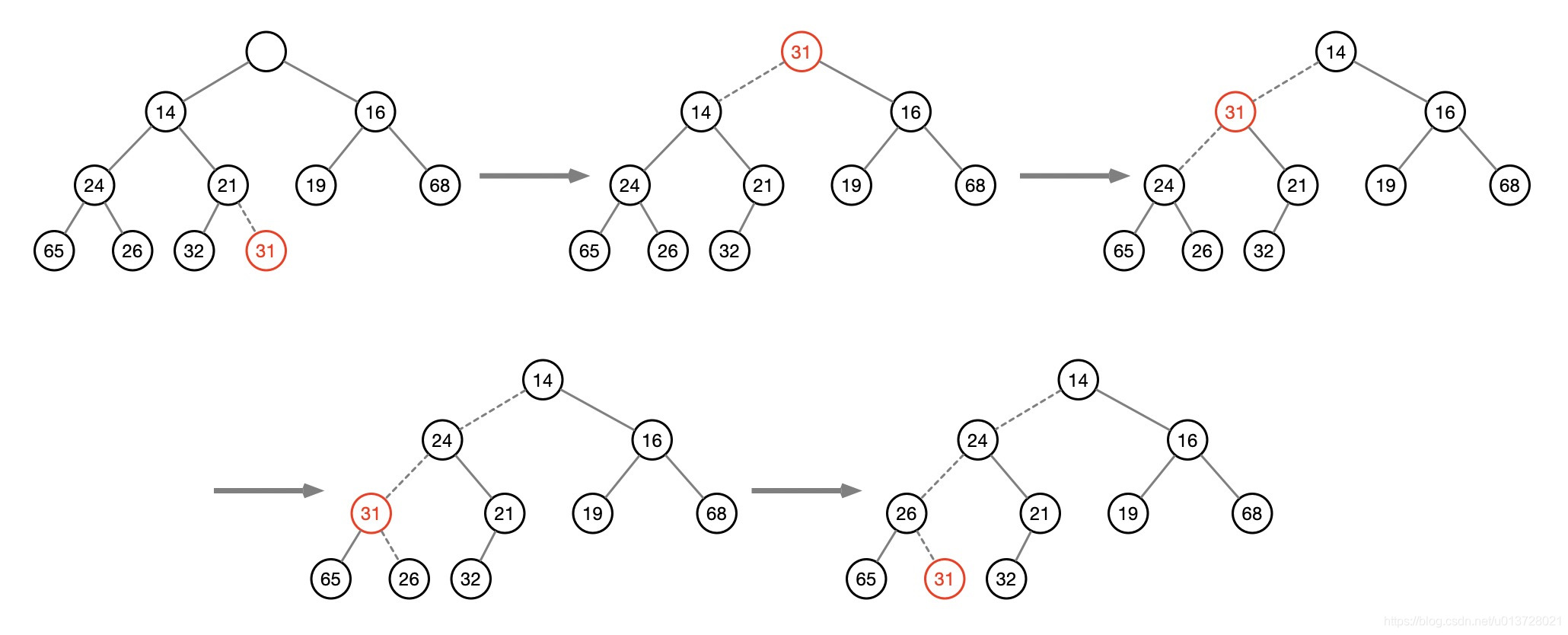
• 上浮操作

把新插入的元素一层层地上浮，直到找到属于自己的位置，这个操作称之为上浮操作。
可以依次遍历数组，就好比不断往堆中插入新元素，直至遍历结束，这样我们就完成了建堆

//上浮操作代码。
//代码中是小的元素上浮，可用于构建大根堆
public void swim (int index) {while (index > 1 && nums[index/2] > nums[index]) {swap(index/2,index);//交换index = index/2;}
}

• 下沉操作
  从最后一个非叶子节点开始遍历到根节点，每次遍历到的节点与孩子节点中最小（最大）的那个交换，交换后再判断是否还需要继续下沉，判断是否继续主要有两个情况：待下沉元素小于（大于）两个子节点，此时符合堆的规则，无需下沉。或者下沉为叶子节点，此时没有子节点。

//下沉操作
//代码为小的元素下沉，可构建小根堆
public void sink (int[] nums, int index,int len) {while (true) {//获取子节点int j = 2 * index;if (j < len-1 && nums[j] < nums[j+1]) {j++;}//交换操作，父节点下沉，与最大的孩子节点交换if (j < len && nums[index] < nums[j]) {swap(nums,index,j);} else {break;} //继续下沉index = j;}}

2. 排序
   先将堆顶元素与堆的最后一个元素进行交换，然后将新的堆顶元素执行下沉操作。重复执行上述步骤直至完全有序。

//完整代码（建堆+排序）
//大根堆还是小根堆需要更改代码中下沉的大小判断条件，下面代码是小根堆代码
class Solution {public int[] sortArray(int[] nums) {int len = nums.length;int[] a = new int[len + 1];for (int i = 0; i < nums.length; ++i) {a[i+1] = nums[i];}          //下沉建堆for (int i = len/2; i >= 1; --i) {sink(a,i,len);}int k = len;//排序while (k > 1) {swap(a,1,k--);sink(a,1,k);}for (int i = 1; i < len+1; ++i) {nums[i-1] = a[i];}return nums;}public void sink (int[] nums, int k,int end) {//下沉while (2 * k <= end) {int j = 2 * k;//找出子节点中最大或最小的那个if (j + 1 <= end && nums[j + 1] > nums[j]) {j++;}if (nums[j] > nums[k]) {swap(nums, j, k);} else {break;}k = j;}}public void swap (int nums[], int i, int j) {int temp = nums[i];nums[i] = nums[j];nums[j] = temp;}}

时间复杂度分析
因为我们建堆的时间复杂度为 O(n），排序过程的时间复杂度为 O(nlogn)，所以总的时间复杂度为 O(nlogn)。

空间复杂度分析
这里需要注意，我们上面的描述过程中，为了更直观地描述，空出数组的第一位，这样我们就可以通过 i * 2 和 i * 2+1 来求得左孩子节点和右孩子节点 。

我们也可以根据 i * 2 + 1 和 i * 2 + 2 来获取孩子节点，这样则不需要临时数组来处理原数组，将所有元素后移一位，所以堆排序的空间复杂度为 O(1)，是原地排序算法。

稳定性分析
堆排序不是稳定的排序算法，在排序的过程，我们会将堆的最后一个节点跟堆顶节点交换，改变相同元素的原始相对位置。

最后我们来比较一下快速排序和堆排序。
1.对于快速排序来说，数据是顺序访问的。而对于堆排序来说，数据是跳着访问的。这样对 CPU 缓存是不友好的。
2.相同的的数据，排序过程中，堆排序的数据交换次数要多于快速排序。