【堆】堆的实现（Java）

article/2025/11/7 13:45:00

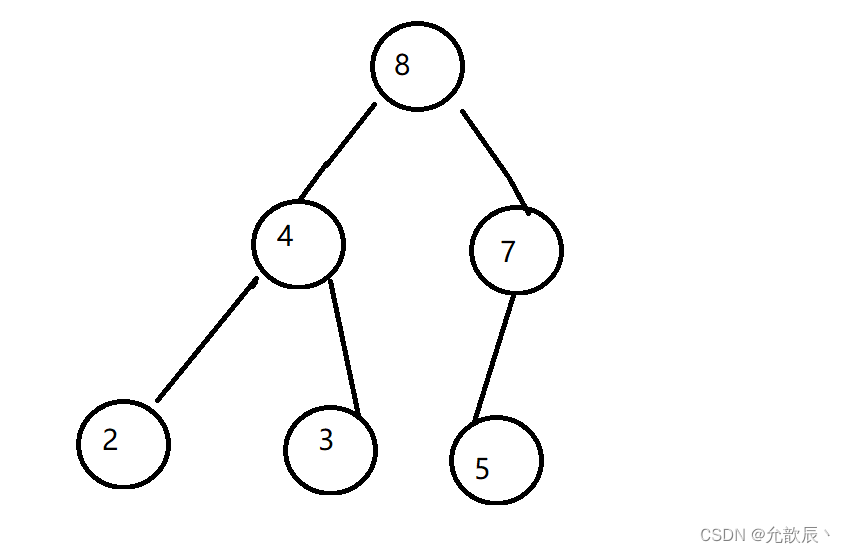
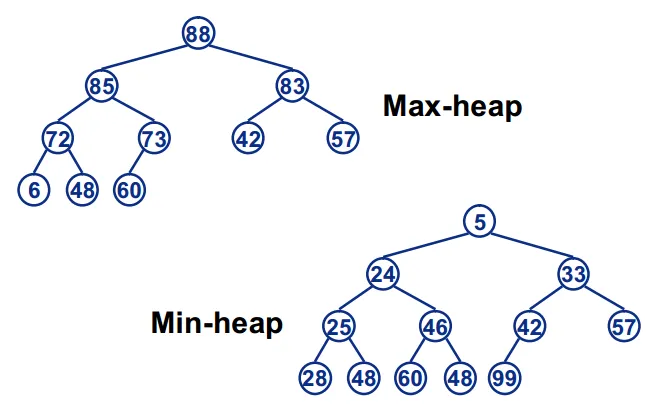
今天学习堆这种数据结构。堆通常是一个可以被看做一棵树的数组对象。堆总是满足下列性质：

堆中某个结点的值总是不大于或不小于其父结点的值；
堆总是一棵完全二叉树。

将根结点最大的堆叫做最大堆或大根堆，根结点最小的堆叫做最小堆或小根堆。

1.用优先队列实现

一般我们直接用优先队列实现堆：

// 小顶堆，以 Integer 为例
PriorityQueue<Integer> pq = new PriorityQueue<>();
// 大顶堆
PriorityQueue<Integer> pq = new PriorityQueue<>((o1, o2) -> o2 - o1);
PriorityQueue<Integer> pq = new PriorityQueue<>(new Comparator<Integer>() {@Overridepublic int compare(Integer o1, Integer o2) {return o2 - o1;}});

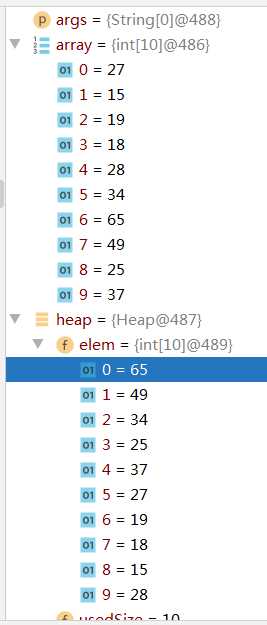
2.用数组实现

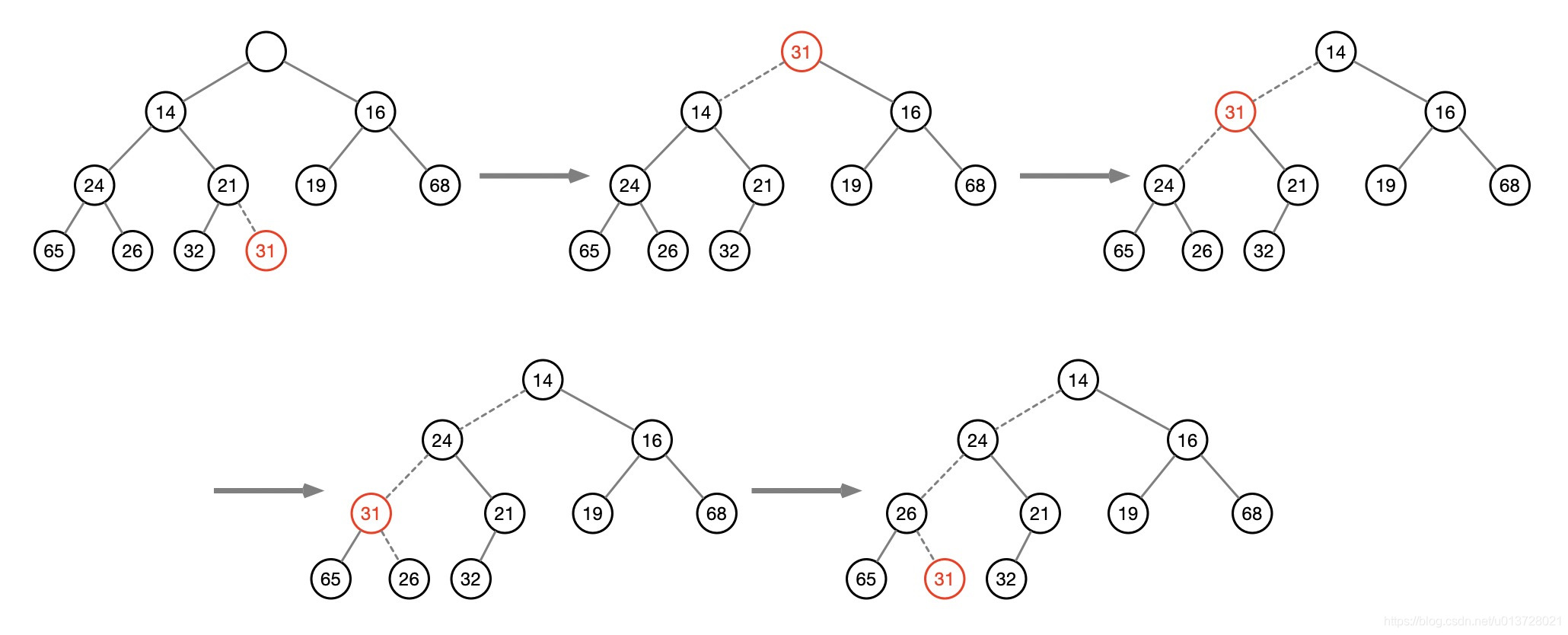
我们可以通过自己定义数组以及调整方法来实现堆。对于完全二叉树，用数组存储时，数组中下标为 i 的元素，其左孩子是 2i，右孩子是 2i+1，于是可以得到下面的实现：

public class Main {private final static int len = 101;  // 堆的最大容量，下标从 1 开始，因此len 比元素总数多一个private static int n = 0;	// 堆中元素的个数private static int[] heap = new int[len];// 向下调整，时间复杂度 O(logn)public static void downAdjust(int low, int high) {int i = low, j = i * 2;while (j <= high) {if (j + 1 <= high && heap[j + 1] > heap[j]) {j = j + 1;      // 右孩子更大}if (heap[j] > heap[i]) {    // 孩子比父节点大int temp = heap[i];heap[i] = heap[j];heap[j] = temp;i = j;j = i * 2;} else {    // 不需要调整提前结束break;}}}// 建堆，时间复杂度O(n)public static void createHeap() {for (int i = n / 2; i >= 1; i--) {downAdjust(i, n);}}// 删除堆顶元素，时间复杂度O(logn)public static int deleteTop() {int top = heap[1];heap[1] = heap[n--];downAdjust(1, n);return top;}// 向上调整，时间复杂度O(logn)public static void upAdjust(int low, int high) {int i = high, j = i / 2;while (j >= low) {if (heap[j] < heap[i]) {    // 父节点更小，需要调整int temp = heap[i];heap[i] = heap[j];heap[j] = temp;i = j;j = i / 2;} else {break;}}}// 添加元素public static void insert(int x) {heap[++n] = x;upAdjust(1, n);}public static void main(String[] args) {int[] nums = new int[]{4, 3, 7, 8, 2, 1, 9, 6, 5};// 测试 insertn = 0;for (int num : nums) {insert(num);}while (n != 0) {System.out.print(deleteTop() + " ");}System.out.println();// 测试 createHeapn = nums.length;for (int i = 0; i < n; i++) {heap[i + 1] = nums[i];}createHeap();while (n != 0) {System.out.print(deleteTop() + " ");}}
}

3.练习：力扣373. 查找和最小的 K 对数字

给定两个以升序排列的整数数组 nums1 和 nums2 , 以及一个整数 k 。

定义一对值 (u,v)，其中第一个元素来自 nums1，第二个元素来自 nums2 。

请找到和最小的 k 个数对 (u1,v1), (u2,v2) … (uk,vk) 。

示例 1:

输入: nums1 = [1,7,11], nums2 = [2,4,6], k = 3
输出: [1,2],[1,4],[1,6]
解释: 返回序列中的前 3 对数：[1,2],[1,4],[1,6],[7,2],[7,4],[11,2],[7,6],[11,4],[11,6]

示例 2:

输入: nums1 = [1,1,2], nums2 = [1,2,3], k = 2
输出: [1,1],[1,1]
解释: 返回序列中的前 2 对数：[1,1],[1,1],[1,2],[2,1],[1,2],[2,2],[1,3],[1,3],[2,3]

示例 3:

输入: nums1 = [1,2], nums2 = [3], k = 3 
输出: [1,3],[2,3]
解释: 也可能序列中所有的数对都被返回:[1,3],[2,3]

用优先队列实现堆：

class Solution {public List<List<Integer>> kSmallestPairs(int[] nums1, int[] nums2, int k) {// 定义一个堆，大小为 kPriorityQueue<int[]> heap = new PriorityQueue<>(k, new Comparator<int[]>(){@Overridepublic int compare(int[] idx1, int[] idx2) {return nums1[idx1[0]] + nums2[idx1[1]] - nums1[idx2[0]] - nums2[idx2[1]];}});List<List<Integer>> result = new ArrayList<>();int m = nums1.length;int n = nums2.length;// 假设上一个被选择的是[mi, nj],由于 m 和 n 是递增的// 那么下一个一定是 [mi+1, nj] 或者 [mi, nj+1]// 所以先把 m 的每个元素和 n0 组合，加进去，下次加入只需要将 n 的下标加 1 即可for (int i = 0; i < Math.min(m, k); i++) {heap.offer(new int[]{i, 0});}while (k-- > 0 && !heap.isEmpty()) {int[] idx = heap.poll();result.add(Arrays.asList(new Integer[]{nums1[idx[0]], nums2[idx[1]]}));if (idx[1] + 1 < n) {heap.offer(new int[]{idx[0], idx[1] + 1});}}return result;}
}