实验八、连续系统的复频域分析
- 一、实验目的
- 二、实验器材
- 三、实验原理
- 1、用MATLAB进行Laplace正、反变换
- 例1:分别用Laplace和ilaplace函数求
- 2、用MATLAB进行部分分式展开
- 3、用MATLAB分析LTI系统的特性
- 三、实验内容
- 1、验证实验原理中所述的相关程序;
- 2、求信号的拉普拉斯变换
- 3、求函数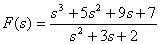的反变换
- 四、 实验报告要求
- 1.简述实验目的和实验原理;
- 2.写出其对应的matlab程序;
- 3.上机调试程序的方法及实验中的心得体会。
一、实验目的
1、学会用matlab进行Laplace正、反变换;
2、掌握用matlab进行部分分式展开;
3、掌握用matlab分析LTI系统的特性。
4、掌握系统函数的零、极点分布与系统的稳定性之间的关系。
二、实验器材
计算机、MATLAB软件
三、实验原理
1、用MATLAB进行Laplace正、反变换
MATLAB的符号数学工具箱提供了计算Laplace正、反变换的函数Laplace和ilaplace,其调用格式为
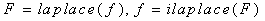
上述两式右端的f和F分别为时域表示式和s域表示式的符号表示,可以应用函数sym实现,其调用格式为 S=sym(A)
式中,A为待分析表示式的字符串,S为符号数字或变量。
例1:分别用Laplace和ilaplace函数求
(1)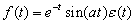 的Laplace变换;
的Laplace变换;
(2)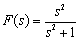 的Laplace反变换。
的Laplace反变换。
(1) matlab 程序如下
f=sym('exp(-t)*sin(a*t)');
F=laplace(f)
或
syms a t
F=laplace(exp(-t)*sin(a*t))
运行结果:
F =
a/((s+1)^2+a^2)
(2)matlab 程序如下
F=sym('s^2/(s^2+1)');
ft=ilaplace(F)
或
syms s
ft= ilaplace(s^2/(s^2+1))
运行结果
ft =
dirac(t)-sin(t)
2、用MATLAB进行部分分式展开
用MATLAB函数residue可以得到复杂有理分式F(s)的部分分式展开式,其调用格式为
[r,p,k] = residue(num,den)
其中,num,den分别为F(s)的分子和分母多项式的系数向量,r为部分分式的系数,p为极点,k为F(s)中整式部分的系数,若F(s)为有理真分式,则k为零。
例2:用部分分式展开法求F(s)的反变换
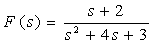
matlab 程序如下
clear all
format rat; %将结果数据以分数形式显示
num=[1,2];
den=[1,4,3];
[r,p]=residue(num,den)
运行结果:
r =1/2 1/2 p =-3 -1
F(s)可展开为
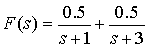
然后根据不同的ROC,可写出F(s)的时域表达式x(t)。
第一种情况,ROC为 Re{s} < -3,则f(t)为反因果信号,其数学表达式为
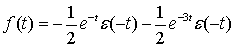
第二种情况,ROC为 -3< Re{s} < -1,则f(t)为双边非因果信号,其数学表达式为
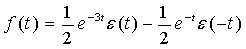
第三种情况,ROC为 Re{s} >-1 ,则f(t)为因果信号,其数学表达式为
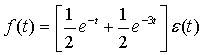
所以,若f(t)为因果信号,则
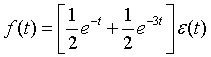
3、用MATLAB分析LTI系统的特性
系统函数H(s)通常是一个有理分式,其分子和分母均为多项式。系统函数的零极点图能够直观地表示系统的零点和极点在s平面上的位置,从而比较容易分析系统函数的收敛域和稳定性。
对于一个连续时间LTI系统,它的全部特性包括稳定性、因果性和频响特性等完全由它的零极点在s平面上的位置所决定。
计算H(s)的零极点的方法如下
(1)用MATLAB中的roots函数,求出分子和分母多项式的根,然后用plot命令画图。
(2)用MATLAB中的pzmap函数画图。其调用格式为
pzmap(sys)
sys表示LTI系统的模型,要借助tf函数获得,其调用格式为
sys=tf(b,a)
式中,b和a分别为系统函数H(s)的分子和分母多项式的系数向量。
如果已知系统函数H(s),求系统的单位冲激响应h(t)和频率响应H(jω)用以前介绍过的impulse和freqs函数。
例3: 已知系统函数为
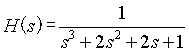
画出其零极点分布图,求系统的单位冲激响应h(t)和频率响应H(jω),并判断是否稳定。
matlab 程序如下
clear all
num=[1];
den=[1,2,2,1];
sys=tf(num,den);
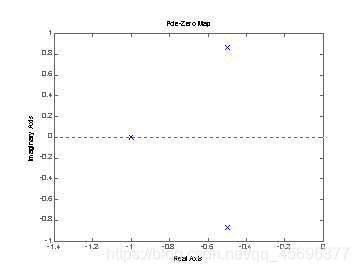
figure(1);pzmap(sys);
t=0:0.02:10;
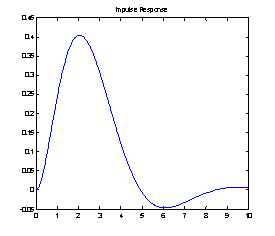
h=impulse(num,den,t);
figure(2);plot(t,h)
title('Impulse Response')
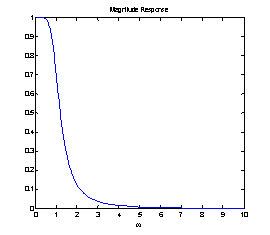
[H,w]=freqs(num,den);
figure(3);plot(w,abs(H))
xlabel('\omega')
title('Magnitude Response')
三、实验内容
1、验证实验原理中所述的相关程序;
2、求信号的拉普拉斯变换
程序如下:
f=sym('t*exp(-3*t)');
F=laplace(f)
运行结果如下:

3、求函数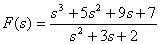 的反变换
的反变换
程序如下:
clear all
format rat; %½«½á¹ûÊý¾ÝÒÔ·ÖÊýÐÎʽÏÔʾ
num=[1,5,9,7];
den=[1,3,2];
[r,p]=residue(num,den)
运行结果如下:

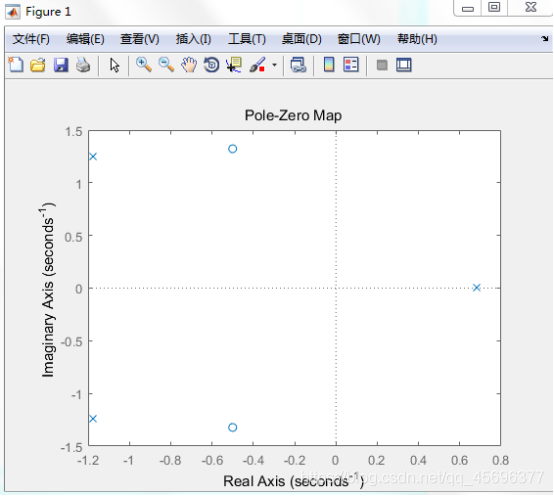
4、已知连续系统的系统函数如下,试用MATLAB绘制系统的零极点图,并根据零极点图判断系统的稳定性
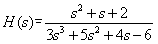
程序如下:
clear all
num=[1,1,2];
den=[3,5,4,-6];
sys=tf(num,den);
figure(1);pzmap(sys);
运行结果如下:
四、 实验报告要求
1.简述实验目的和实验原理;
2.写出其对应的matlab程序;
3.上机调试程序的方法及实验中的心得体会。
通过本次实验,对于利用MATLAB软件进行拉普拉斯变换与逆变换,拉普拉斯变换法求解微分方程;求解系统函数的零极点,分析其分布和时域特性关系;分析系统函数的极点分布与系统稳定性的关系有了更为深刻的理解。
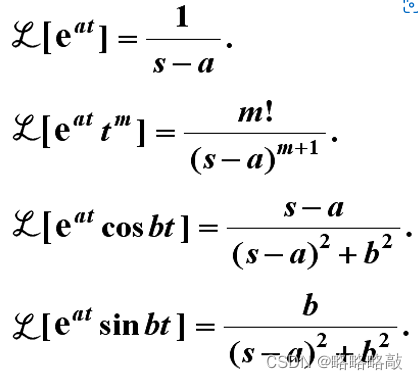


![[Matlab-5]Laplace变换](https://img-blog.csdnimg.cn/20210528100015487.png)