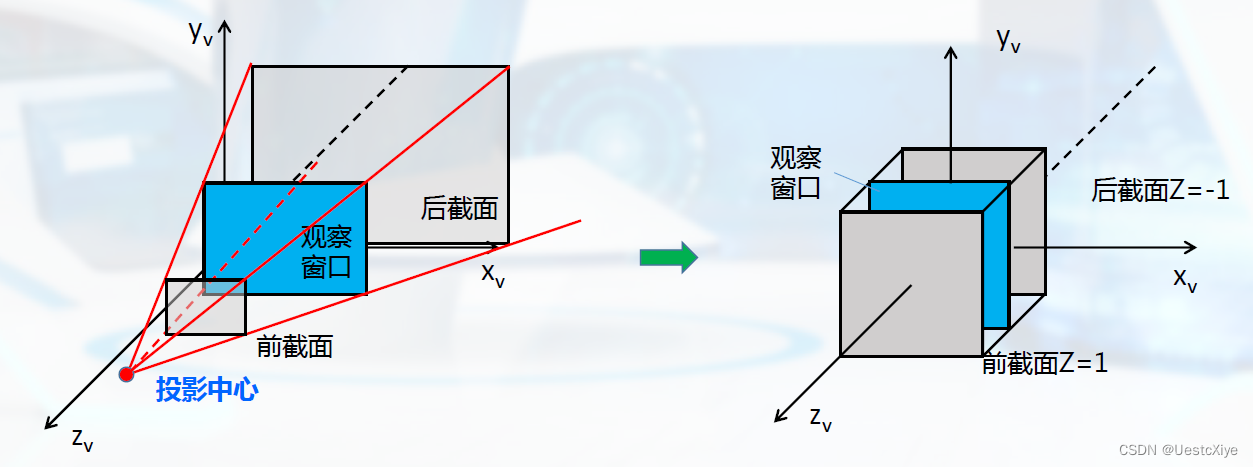
坐标到达观察空间之后,我们需要将其投影到裁剪坐标。裁剪坐标会被处理至-1.0到1.0的范围内,并判断哪些顶点将会出现在屏幕上。
而[-1.0,1.0]构成的正方体又叫规则观察体(Canonical View Volume, CVV)
一、流程
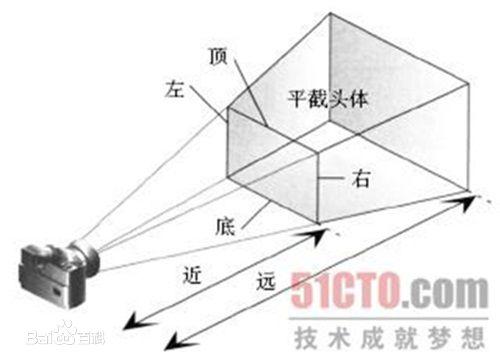
计算机显示器是一个 2D 表面。OpenGL 渲染的 3D 场景必须作为 2D 图像投影到计算机屏幕上。
1、定义投影矩阵,指定了一个范围的坐标,以此来模拟相机的可视范围
2、投影矩阵接着会将在这个指定的范围内的坐标变换为标准化设备坐标的范围(-1.0, 1.0)。所有在范围外的坐标不会被映射到在-1.0到1.0的范围之间,所以会被裁剪掉。以此模拟相机的可视范围。
2、裁剪完后,进行透视除法,将4D裁剪空间坐标变换为3D标准化设备坐标。
二、正交投影
1、创建一个正射投影矩阵需要指定可见平截头体的宽、高和长度。在使用正射投影矩阵变换至裁剪空间之后处于这个平截头体内的所有坐标将不会被裁剪掉。
如下所示,左边为平截头体,右边为CVV,注意:
2、正交投影的变换矩阵可以理解为先将平截头体的中心平移到坐标系原点,再进行缩放

如上图所示,右边为平移,左边为缩放。注意图片中平移矩阵的第三行,来自闫大神的GAMES101(未考虑实际坐标,第三行带负号),Opengl实际上为第一张图,即z坐标为-n~-f,因此不带负号。包括下面透视投影第一种方式也作了相应改变。
2、正交投影没有远近之分,所以w为1,透视除法不改变方向,不翻转坐标系,直接对应理想的图像坐标系
三、透视投影
透视投影有两种理解方式:一、看成透视到正交,再正交投影变换;二、针孔模型的透视投影
第一种方式
如下所示,先将透视投影指定的平截头体变形成正交投影中的平截头体

可以看到,透视投影把所有通过原点(眼睛)的直线映射到平行于z轴的直线上,而并不移动z=n平面中直线上点的位置,如下所示。
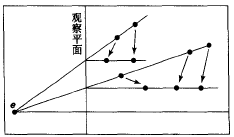
变换过程中需要铭记两点:1、变换前后近平面的点始终在近平面上;2、变形前后远平面的点始终在远平面上;如下所示。
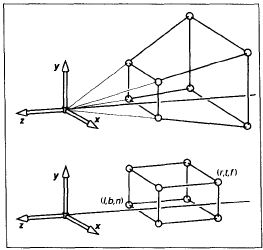
根据第1、2点,且正交投影中平截头体的一条平行线在近平面、远平面的交点的x、y坐标相等,有

近平面的交点(x’,y’,z’)和远平面的蓝点(点(x,y,z)变形之后)的x、y坐标相等,由相似三角形得到:
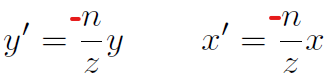
由齐次坐标表示这一过程:

乘以-z是因为透视除法要将裁剪空间的右手坐标系变为NDC空间的左手坐标系,同时保留深度信息,所以将w设为-z。可以得到透视到正交的变换矩阵,
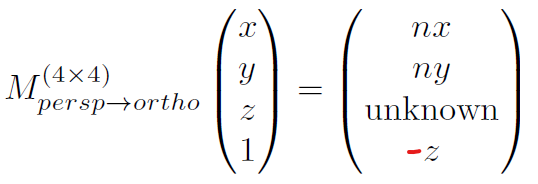

第三行的求解借助了变换过程中的上述两点,由近平面的点不变可以得到,近平面的z坐标为-n

可以看到,第三行不含x、y,因此必是(0,0,A,B)
同理,由远平面的点始终在远平面得到,远平面的z坐标为-f
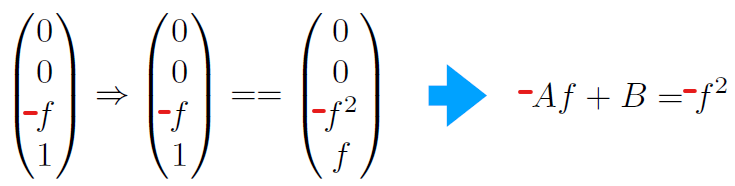

因此变换矩阵为
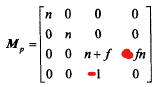
完整投影矩阵如下

第二种方式
根据针孔相机的成像原理,将透视投影的平截头体变换到CVV

在OpenGL中,观察空间中的3D点被投影到近平面(投影平面)上。投影过程如下所示。

(Xe,Ye,Ze)为观察空间中的3D点坐标,(Xp,Yp,Zp)为投影点的坐标。由相似三角形得到,
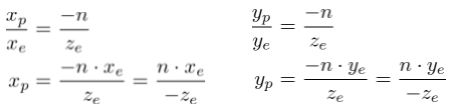
(Xc,Yc,Zc,Wc)为裁剪空间的齐次坐标,Wc设为-z的原因上面已有说明。
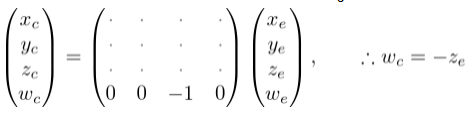
将Xp和Yp以线性关系映射到NDC的Xn和Yn,[l,r]=>[-1,1]和[b,y]=>[-1,1]
由线性归一化的等比例性质,有
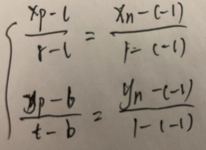
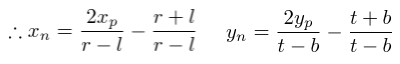
将Xp和Yp代入上述方程
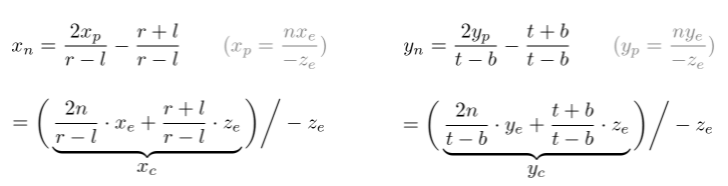
从上述方程中,可以得到投影矩阵的第一、二行
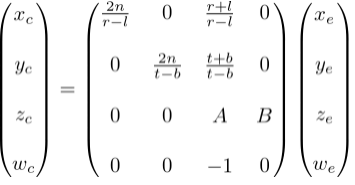
NDC空间是由裁剪空间经过透视除法得到的,所以有
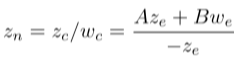
而在观察空间中,We=1,所以
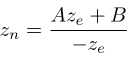
Ze:[-n,-f];Zn:[-1,1];-n -> -1;-f -> 1,所以有
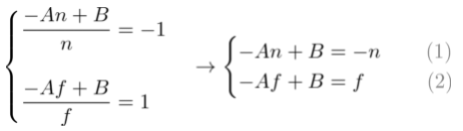
求解得到
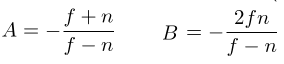
完整投影矩阵如下:

四、OpenGL和OpenCV结合
首先,需要明白OpenGl的透视投影模型和普通相机的小孔投影模型是类似的,其投影矩阵对应于相机的内参矩阵K,观察矩阵对应于相机的外参矩阵[R|T]。但是,我们之前求得的K和[R|T]还不能直接使用,原因有二,其一,OpenGL投影模型使用的坐标系与OpenCV的不同;其二,OpenGL为了进行Clipping,其投影矩阵需要将点投影到NDC空间中。
OpenGL的相机坐标系相当于OpenCV的相机坐标系绕着X轴旋转了180度,因此只需要左乘一个旋转矩阵即可,如下:
[ 1, 0, 0,
0, 1, 0,
0, 0, -1 ]
而对于投影矩阵,不仅要有与内参矩阵K相同的透视效果,还得把点投影到NDC中
内参矩阵K形式如下:
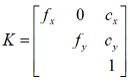
fx、fy代表像距(fx、fy一般相等,以下为方便与远平面f区分,用focal表示),cx、cy表示理想的图像坐标系原点在像素坐标系下的坐标
注意,在计算机视觉中,一般把f称为焦距,其实是不准确的,在摄影测量学中更准确的表达是像距(主距),即焦点到像平面的距离。焦距实际上是光学中心到焦点的距离。
然后,观察空间的三维点是投影到像平面的,需要注意近平面、远平面和像平面的区分。在OpenGL中,近、远平面到原点的距离是由用户指定,默认近平面就是像平面,到原点的距离是n。而提供了内参矩阵后,像平面到原点的距离为focal,根据到原点的距离从近到远排序:近平面<像平面<远平面。
所以,针对透视投影的第二种方式,因为投影矩阵的第一、二行是先由观察空间的三维点和投影点的相似三角形得到Xp和Xe的对应关系,再由线性归一化的等比例性质得到Xn和Xp的对应关系,推导出来的,而此时投影点的z坐标不再是-n,而是-focal(像距),因此
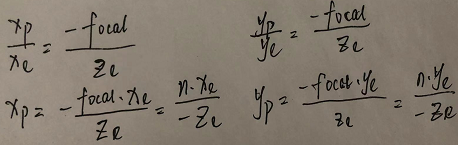
投影矩阵的第三行是由Zn、Zc、Ze的边界值的对应关系得到的,与像平面无关,所以不需要改变
最终的投影矩阵只需要将第一、二行中的n换成focal即可

参考
[1]OpenGL Projection Matrix
[2]深入探索透视投影变换
[3]坐标系统
[4]OpenGL与OpenCV实现增强现实
[5]GAMES101
[6]Fundamentals of Computer Graphics (4th Edition)
[7]焦平面、像平面、主距、焦距辨析
PS:目前还不会用LaTeX,公式之类的只能手写,过一段时间学会了再来更新(如果还记得的话)