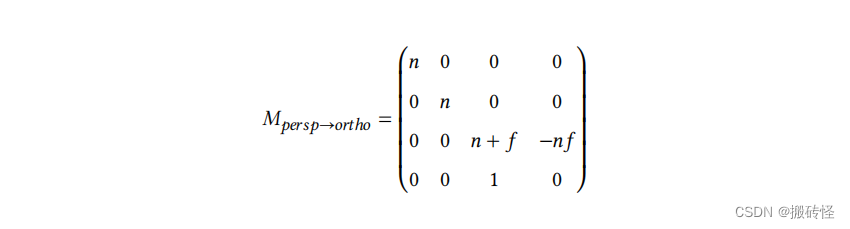1.视图变换
在 3 维物体变到二维平面的过程中,我们需要规定好相机的位置。对于相机所做的变换就是视图变换
(Viewing/Camera transformation)。
我们需要对相机位置进行定义,对于一个相机我们要规定下面三个属性:
- 相机位置(视点)(Position)
- 相机拍摄方向(视线)(Look-at/Gaze direction)
- 相机向上方向(Up direction,假设垂直于 look-at direction)
根据相对运动我们可以知道,只要相机和被拍摄物体相对位置不变,那么拍摄出来的照片应当是一样
的。我们可以通过对被拍摄物体做相同的变换来把相机变换到标准位置。相机的标准位置为
- 相机位置在原点 (0, 0);
- 相机拍摄方向是-z 轴方向;
- 相机的向上方向是 y 轴方向。
将任意位置的相机移动到标准位置需要以下操作:
- 将摄像机中心点移动到原点;
- 把视线旋转到-z轴方向;
- 把上方向旋转到y轴方向;
平移变换的变换矩阵可以写作:
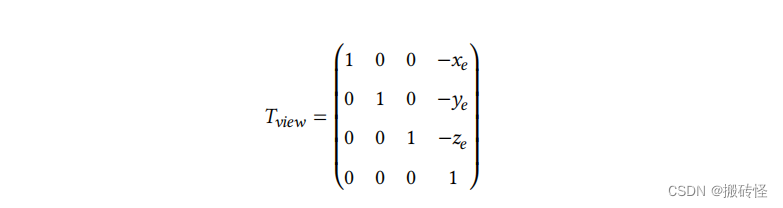
旋转矩阵的写法比较麻烦。从 ̂𝑔 旋转到-z 轴方向,𝑡̂旋转到 y 轴方向以及 ̂𝑔 × 𝑡̂旋转到 x 轴方向比较难
写,但是旋转变换的逆变换非常的简单
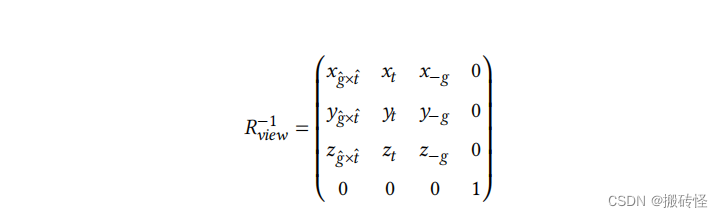
我们用 x 轴方向单位向量 (1, 0, 0, 0),y 轴单位向量 (0, 1, 0, 0),z 轴单位向量 (0, 0, 1, 0) 代入后结果是正确的。我们知道旋转矩阵的逆矩阵是正交矩阵,因此旋转变换矩阵的逆是旋转变换矩阵的转置矩阵。也是说
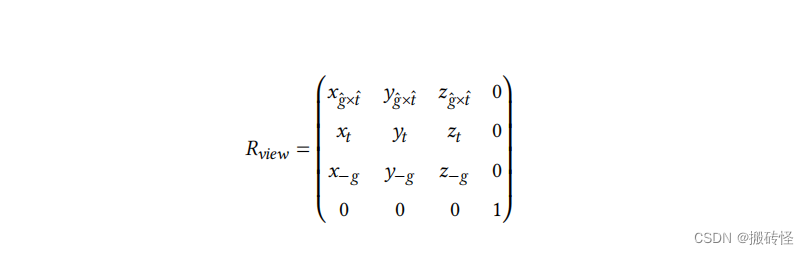

以上就是我们得到的视图变换矩阵。
2.投影变换
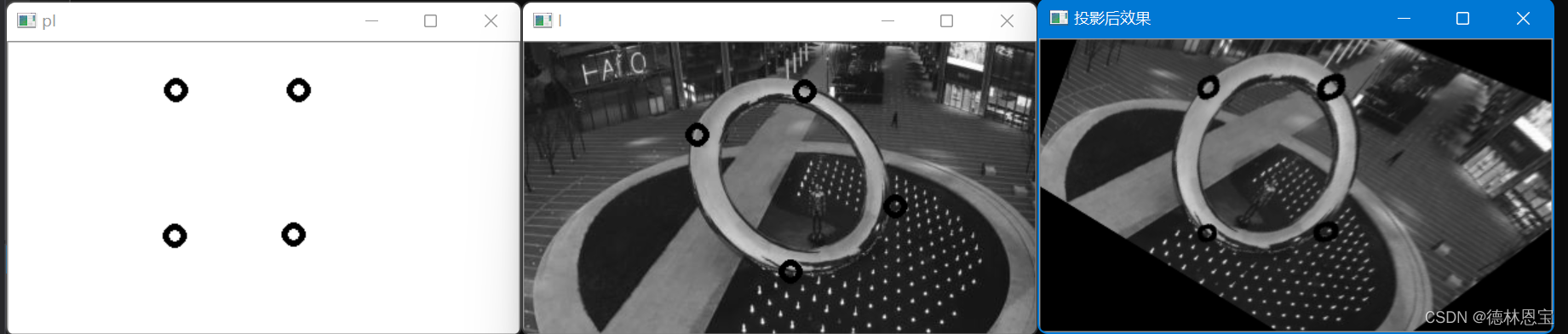
投影变换(Projection transformation)是把 3 维模型投影到 2 维平面的变换。投影变换分为正交投影(Orthographic projection)以及透视投影(Perspective projection)。正交投影中,投影后原本平行的线保持平行关系。但是透视投影中平行的线在投影后不一定能保持平行关系,会相交到某一点上(这也就是近大远小现象)
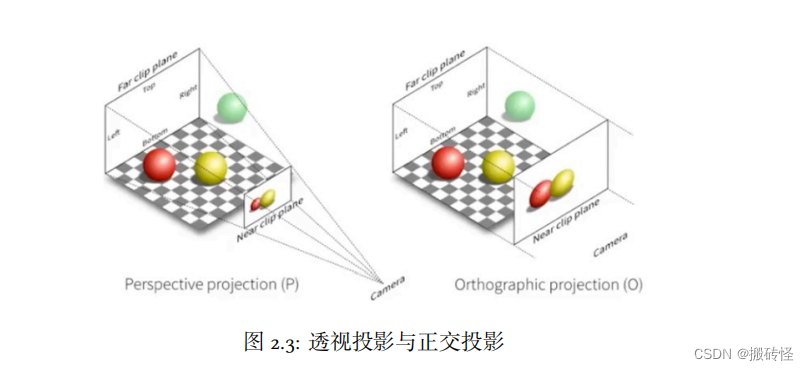
2.1 正交投影
正交投影将相机放在原点上,拍摄方向是-z 轴方向,向上方向是 y 轴方向。只需要去掉 z 轴后,xy 平面
上的图像就是投影结果。为了能够正交投影,我们会把所有模型移动到 [−1, 1]3 的区间范围内。
在空间中描述一个立方体(立方体中包含了所有需要绘制的模型),将立方体变换到 [−1, 1]3 的区间范
围内
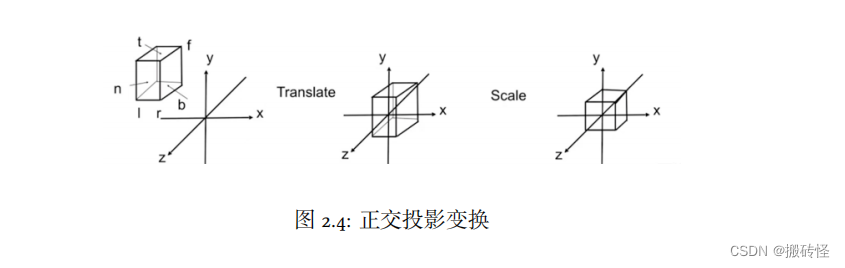
定义空间中的立方体的左右在 x 轴的坐标,上下在 y 轴的坐标,远近在 z 轴的坐标。这个立方体就可以
被描述 [𝑙, 𝑟 ] × [𝑏, 𝑡] × [𝑓 , 𝑛]。对于 z 轴来说,越远 z 值更小,越近 z 值更大。远是小于近的,保证了右手坐标系下从-z 方向看过去 z 值的规律。
将这样的立方体映射到正则/标准/规范(canonical)立方体 [−1, 1]3
变换方法是先将中心平移到原点,之后对每个边进行缩放到大小为 2。
变换矩阵为:
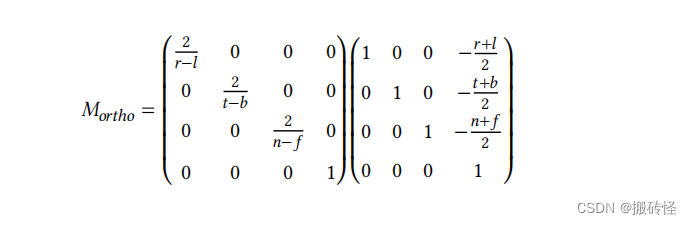
2.2 透视投影
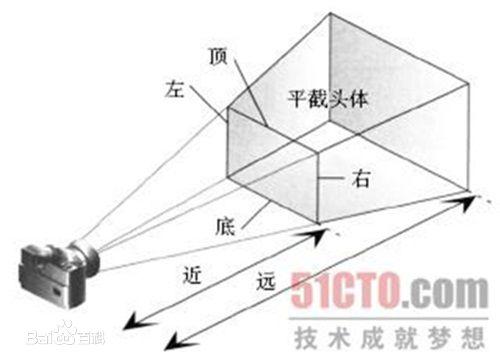
透视投影(Perspective projection)是最为广泛的投影方式。透视投影满足近大远小的性质。接下来我们定义视锥。视锥就是一个透视相机渲染时能看到区域的形状,相机放在平面的中心,一个视锥包含 4 个元素:
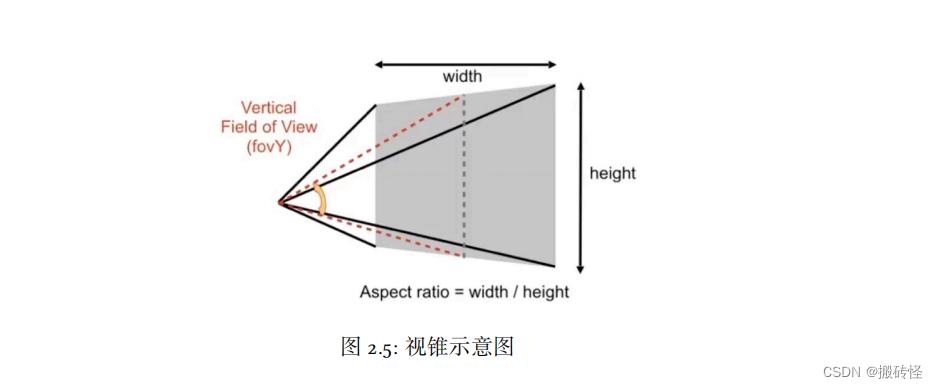
- 近平面:渲染的区域里相机最近的平面;
- 远平面:渲染的区域里相机最远的平面;
- 视野(Field of view,FOV):平面顶部和底部中心到相机连线的夹角;
- 宽高比:平面宽度和高度之比。
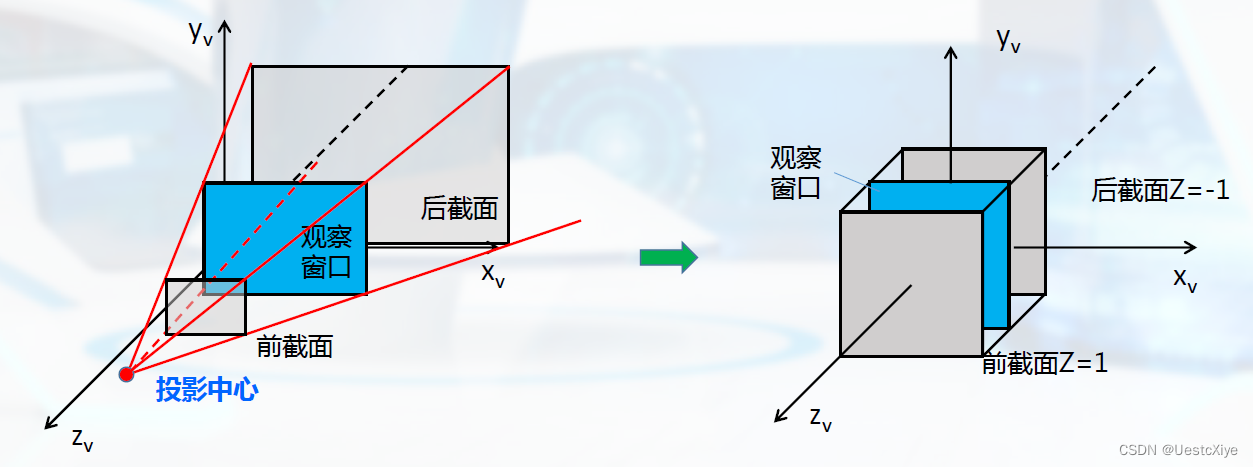
从一个点射出的四棱锥定义了远和近两个平面。我们可以把远平面缩小成和近平面一样大的长方形,
这样视锥就会变成一个立方体。再做一次正交投影就可以得到最终的投影结果了。
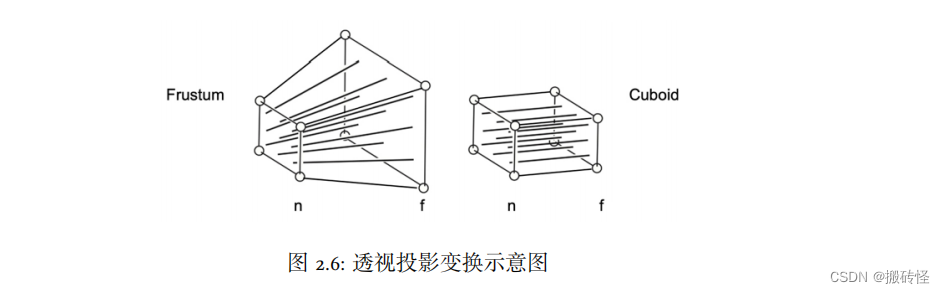
我们需要对这些点进行变换,变换满足三个条件:
- 任何一个在近平面上的点不会发生变化;
- .远平面处的点 z 值不发生变化;
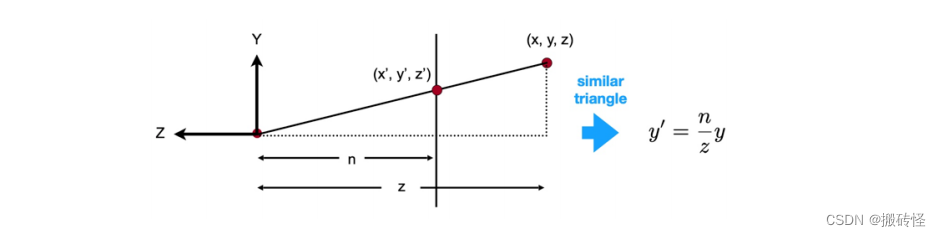
从 YZ 平面看过去,对于远平面上的点 (𝑥, 𝑦, 𝑧) 在投影变换后,根据相似三角形的性质,点的位置变为
( 𝑛𝑧𝑥,𝑛𝑧𝑦, 𝑧)。对于任意一个点点 (𝑥, 𝑦, 𝑧) 来说,变化过程为:
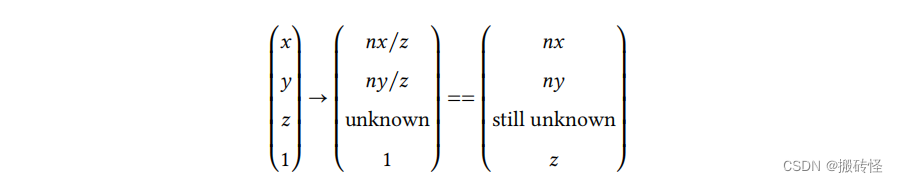
中间点的 z 值变化目前是不确定的。但是对于以上的变化结果我们可以得到变换矩阵的部分结果:
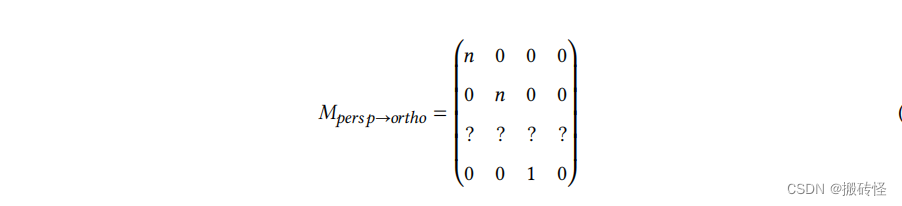
接下来求出未知量。对于近平面的上的点,应当满足变换:
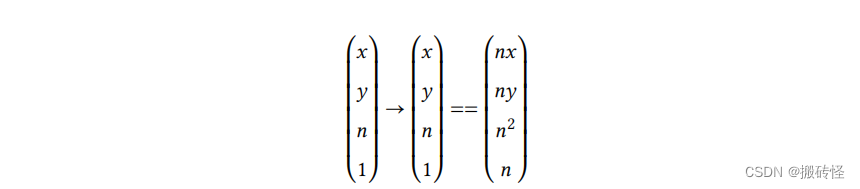
因此可以得到方程:
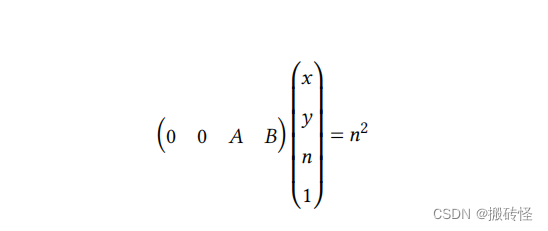
𝑛2 显然和 x,y 的值没有什么关系,因此 x,y 的系数为 0。但是方程不能解出,还需要一个方程。
对于远平面,我们选择中心点,变换应当满足:
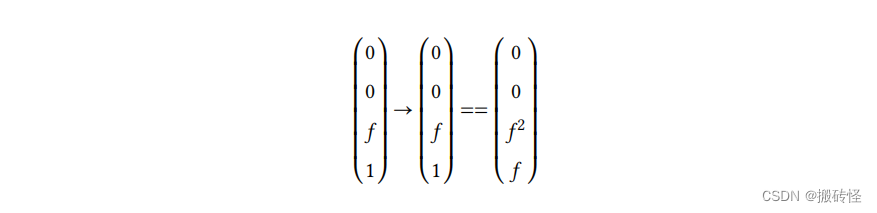
可以得到方程:
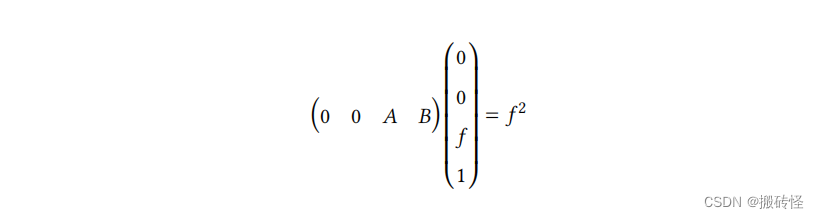
方程展开后可以得到:
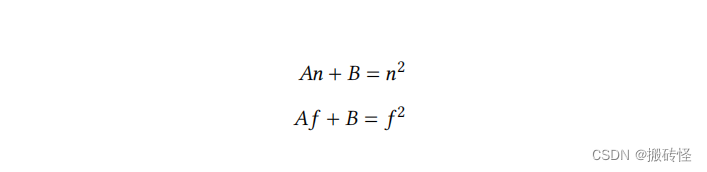
解得:
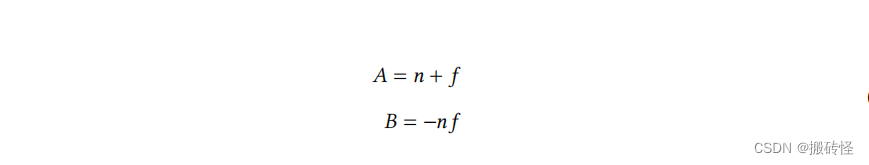
因此我们就解出了变换矩阵: