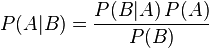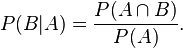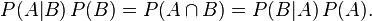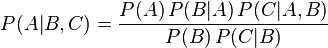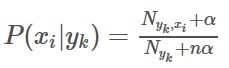基本贝叶斯定理

贝叶斯定理是关于随机事件A和B的 条件概率（或 边缘概率）的一则定理。

其中P(A|B)是在B发生的情况下A发生的可能性。

在贝叶斯定理中，每个名词都有约定俗成的名称：

• P(A)是A的先验概率或边缘概率。之所以称为"先验"是因为它不考虑任何B方面的因素。
• P(A|B)是已知B发生后A的条件概率，也由于得自B的取值而被称作A的后验概率。
• P(B|A)是已知A发生后B的条件概率，也由于得自A的取值而被称作B的后验概率。
• P(B)是B的先验概率或边缘概率，也作标准化常量（normalized constant）.

按这些术语，Bayes定理可表述为：

后验概率 = (相似度*先验概率)/标准化常量

也就是说，后验概率与先验概率和相似度的乘积成正比。

另外，比例P(B|A)/P(B)也有时被称作标准相似度（standardised likelihood），Bayes定理可表述为：

后验概率 = 标准相似度*先验概率

从条件概率推导贝叶斯定理

根据条件概率的定义。在事件B发生的条件下事件A发生的概率是

。

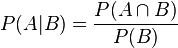同样地，在事件A发生的条件下事件B发生的概率

整理与合并这两个方程式，我们可以找到

这个引理有时称作概率乘法规则。上式两边同除以P(B)，若P(B)是非零的，我们可以得到贝叶斯 定理:

二.Bayes' Rule的推广

对于变量有二个以上的情况，贝式定理亦成立。例如：

这个式子可以由套用多次二个变量的贝式定理及条件机率的定义导出：

。

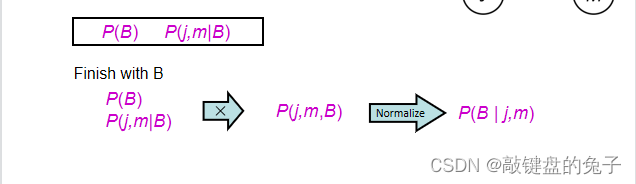
由上述推广，我们可以得到在PGM中一个经常应用的公式：

用文字叙述可表示为：后验概率 = 似然函数*先验概率