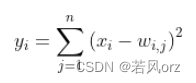从今天开始,带大家从LeNet5开始学习经典的网络模型。
一、LeNet-5
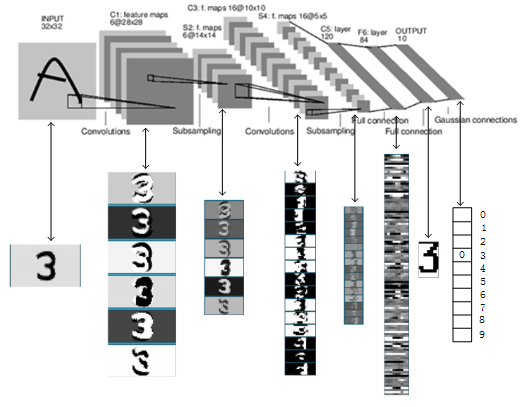
LeNet-5是LeNet系列的最终稳定版,它被美国银行用于手写数字识别,该网络有以下特点:
- 所有卷积核大小均为5*5,步长为1;
- 所有池化方法为平均池化;
- 所有激活函数采用Sigmoid
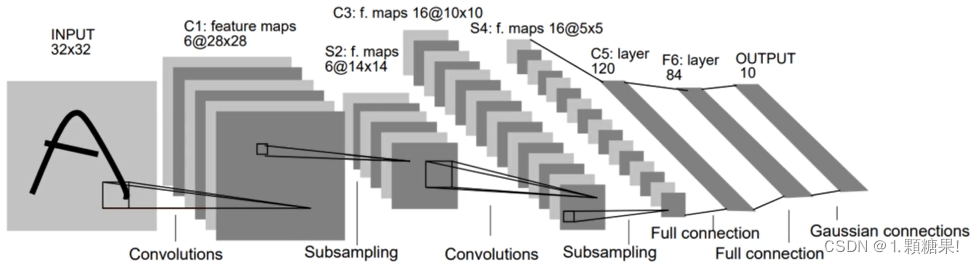
1.输入层:输入图像的尺寸统一归一化为32*32.
2.C1层:第一个卷积层
- 输入图片大小:32*32
- 卷积核大小:5*5,步长1,无填充
- 卷积核种类:6
- 输出特征图大小:28*28 32-5+1=28
- 神经元数量:28*28*6=4704
- 可训练参数:(5*5+1)*6=156 其中,1为偏置参数
- 连接数(和输入层的连接数):(5*5+1)*6*28*28=122304
3.S2层-池化层(下采样层)
- 输入特征图大小:28*28
- 采样区域:2*2
- 采样方式:4个输入相加,乘以一个可训练参数,再加上一个可训练偏置。结果通过sigmoid函数。
- 采样种类:6
- 输出特征图大小:14*14
- 神经元数量:14*14*6
- 连接数(和C1层连接):(2*2+1)*6*14*14
- S2中每个特征图的大小是C1中特征图大小的1/4.
4.C3层-第二个卷积层
- 输入:S2中所有6个或者几个特征图组合
- 卷积核大小:5*5
- 卷积核种类:16
- 输出特征图大小:10*10 14-5+1=10
- C3中的每个特征图是连接到S2中的所有6个或者几个特征图的,表示本层的特征图是上一层提取到的特征图的不同组合。存在的一个方式是:C3的前6个特征图以S2中3个相邻的特征图子集作为输入。接下来6个特征图以S2中4个相邻特征图自己为输入。然后的3个以不相邻的4个特征图子集作为输入。最后一个将S2中所有特征图作为输入。输出的16个通道并没有与输入的每个通道相连。这样设计的初衷有两个:
- 1.减小计算量;
- 2.打破对称性。
- 现在的网络设计中,很少会遵循这样的设计原则。
- 可训练参数:6*(3*5*5+1)+6*(4*5*5+1)+3*(4*5*5+1)+1*(6*5*5+1)=1516
- 连接数:10*10*1516=151600
5.S4层-池化层(下采样层)
- 输入:10*10
- 采样区域:2*2
- 采样方式:4个输入相加,乘以一个可训练参数,再加上一个可训练偏置。结果通过sigmoid函数。
- 采样种类:16
- 输出特征图大小:5*5
- 神经元数量:5*5*16=400
- 连接数:(2*2+1)*400=2000
- S4中每个特征图的大小是C3特征图大小的1/4
6.C5层-第三个卷积层
- 输入:5*5,即S4层的全部16个单元特征图(与S4全相连)
- 卷积核大小:5*5
- 卷积核种类:120
- 输出特征图大小:1*1 (5-5+1)
- 可训练参数:120*(16*5*5+1)=48120
- 连接数:1*1*48120=48120
- C5层是一个卷积层。由于S4层的16个图的大小为5*5,与卷积核的大小相同,所以卷积后形成的图的大小为1*1。这里形成120个卷积结果。每个都与上一层的16个图相连。所以共有(5*5*16+1)*120=48120个连接。
7.F6层-全连接层
- 输入:120维向量
- 输出:84维向量
- 计算方式:计算输入向量和权重向量之间的点积,再加上一个偏置,结果通过sigmoid函数输出。
- 可训练参数:84*(120+1)=10164
8.输出层-全连接层
- 输入:84维向量
- 输出:10维向量
- 可训练参数:84*10,其中10就是分类的类别数。一共有10个节点,分别代表数字0到9,且如果节点i的值为0,则网络识别的结果是数字i。采用的是径向基函数(RBF)的网络连接方式。假设x是上一层的输入,y是RBF的输出,则RBF输出的计算方式是:
下图是LeNet-5识别数字3的过程:
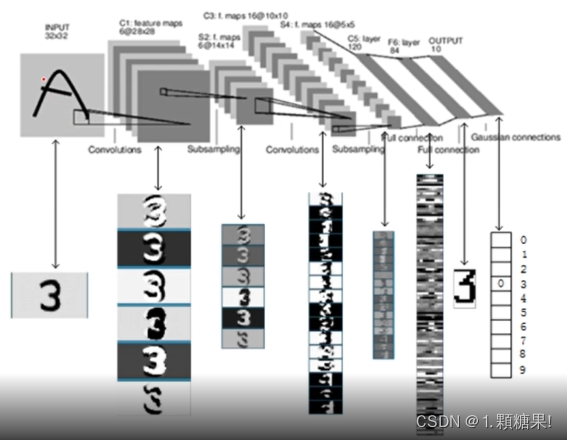
LeNet5的缺点:
输入图像太小,数据不足,在早期并没有在除手写数字识别之外的其他计算机视觉任务上取得大的突破。