一、LeNet-5的背景

LeNet-5诞生于上世纪90年代，是CNN的开山之作，最早的卷积神经网络之一，用于手写数字识别（图像分类任务），它的诞生极大地推动了深度学习领域的发展。LeNet在多年的研究和迭代后，Yann LeCun将完成的这项开拓性成果被命名为LeNet5，并发表在论文《Gradient-Based Learning Applied to Document Recognition》上，如今的AlexNet、ResNet等都是在其基础上发展而来的，在当年是一种用于手写体字符识别的非常高效的卷积神经网络。

二、传统分类算法在图像识别上的弊端

SVM：如果利用SVM算法进行图像分类，首先需要进行人为的特征工程，说白了就是在进行实际的分类任务前，需要去思考如何设计出能够区分图像类别的特征向量，再利用从原始图像抽取出的特征向量，使用支持向量机训练以达到图像分类的目的。暂且不管使用SVM在图像分类的准确率有多好，有一个很明显的问题就是特征向量的提取只能来自于训练样本的映射，这就可能会降低分类模型的泛化性，且提取特征向量的过程耗费很大的人力。另外，特征向量的设计极大的影响了分类效果，模型分类的准确率及其依赖设计的特征的好坏。

全连接神经网络：使用全连接神经网络进行图像分类，虽然极大程度的避免了耗时耗力的人为特征工程工作，但是仍然有非常多的弊端。首先第一个点是，全连接神经网络的输入为1维向量，而图像是2维向量，所以如果我们希望把图像输入进神经网络，必定会将2维图像的直接拉直成1维。我们把图像的三个通道都摊平了，并且塞到了一个1维向量中，那么我们的模型只能学到一个顺序排列的数组的特性，但是图片实际上并不是这样的，一个图像像素跟他上下左右的像素都有关系。2维转1维的过程中直接破坏了图像的空间特征，破坏了平移不变性。还有一个更大的弊端是，模型权重参数数量是千万级别的甚至更多，极大的增大了计算复杂度，并且需要更多的训练样本来保证分类准确度。假设输入图片大小是60x60，即输入是360维的1维向量，再假设全连接神经网络的第一层有100个神经元，那么这里就已经有(360+1)x100=36100个权重了，可想而知计算量有多大！

三、卷积神经网络的3个基本特征

深度神经网络的基本思想是通过构建多层网络，对目标进行多层表示，神经网络能够自动抽取目标对象的抽象特征，以期通过多层的高层次特征来表示数据的抽象语义信息，获得更好的特征鲁棒性。卷积神经网络是一种带有卷积结构的深度神经网络，其中卷积结构可以减少深层网络占用的内存量，相比全连接神经网络在保证精确度的同时降低了计算量，其中包含了三个关键的操作，也就是卷积神经网络的3大基本特征，其一是局部感受野，其二是权值共享，其三是 pooling 层。卷积神经网络的架构十分有效的减少了网络的参数个数，同时缓解了模型的过拟合问题。

四、LeNet-5的网络结构

LeNet-5的网络结构放在如今的深度学习时代不算难，是非常简单的网络结构了，所以非常适合作为对卷积神经网络的入门学习。网络结构图如下：

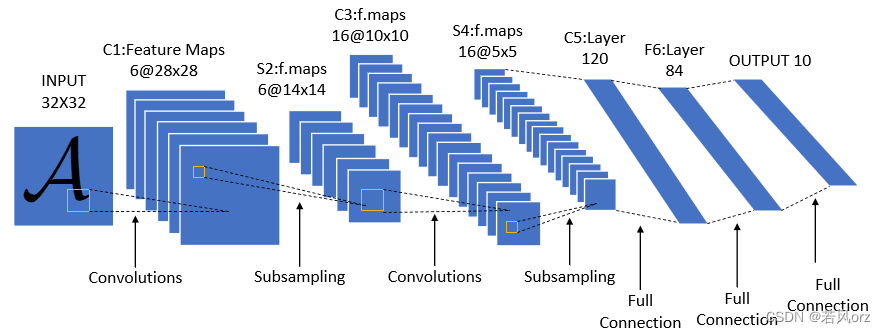
1、Input layer

LeNet-5的输入是一个32×32灰度图像，只有一层通道。

2、Conv1

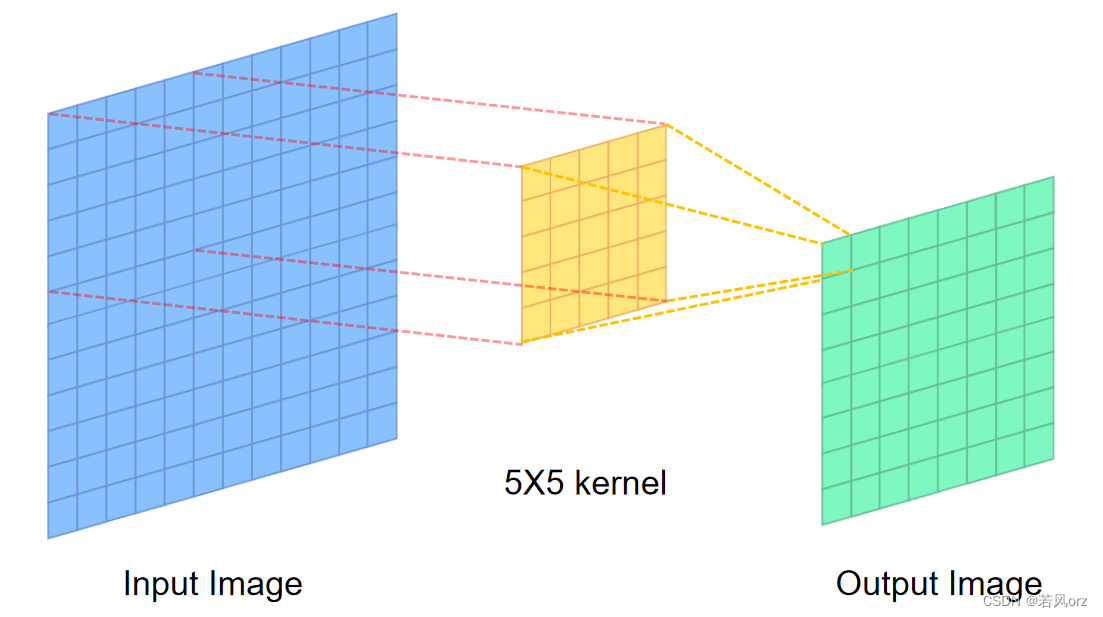
输入图片大小：32x32
卷积核大小：5x5，步长：1，不加padding。
卷积核个数：6
输出特征图大小：28x28
神经元数量：28x28x6
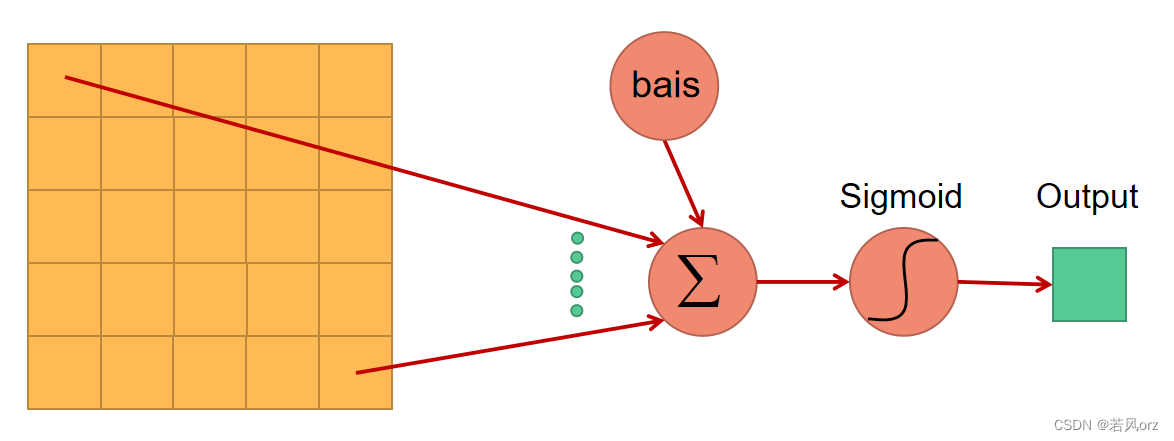
可训练参数为：(5x5+1)x6，“+1”是因为有偏置参数bias
连接数：(5x5+1)x6x28x28=122304，“+1”是因为卷积后的sigmoid激活也视为一次连接

3、Subsampling2

输入特征图大小：28x28
采样区域大小：2x2
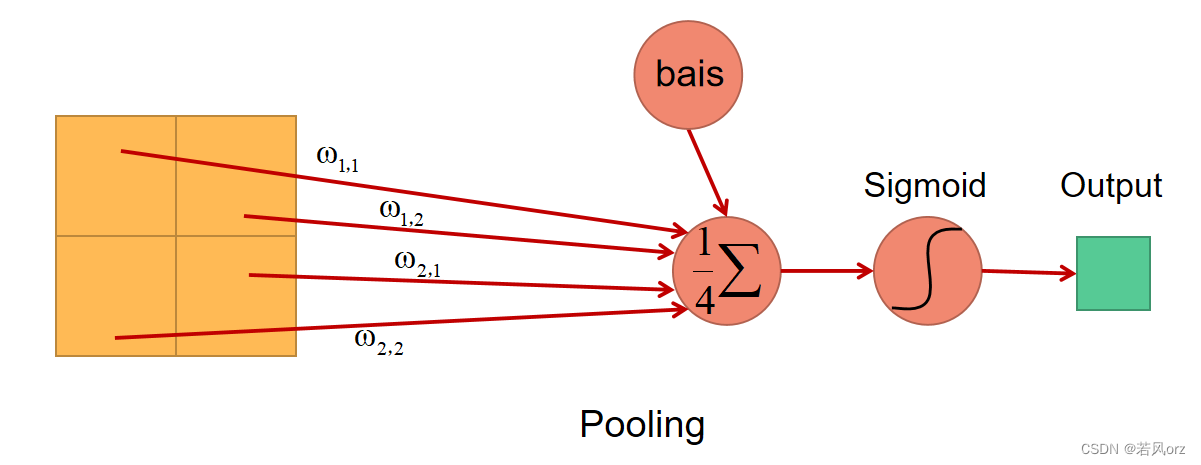
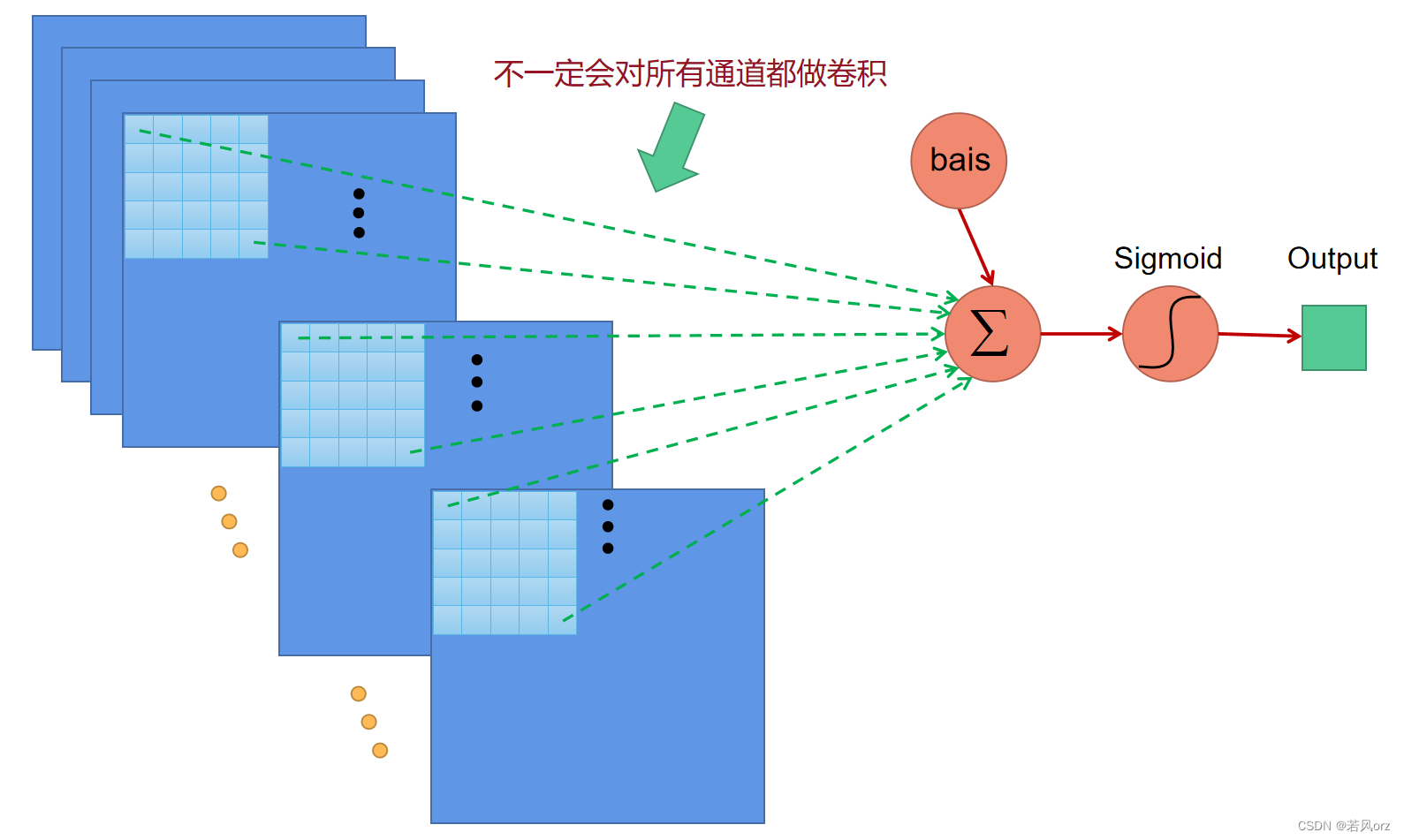
采样方式：4个输入相加，乘以一个可训练参数，再加上一个可训练偏置，结果通过sigmoid函数，步长为2。不理解的话可以看下图。LeNet-5采用方式的pooling方式和average pooling和maximun pooling是不同的，注意区分！！！
采样数量：6，因为有来自上一层的6个特征图
输出特征图大小：14x14
神经元数量：14x14x6
连接数（和Conv1层连接）：(2x2+1)x6x14x14=5880，这里也是一样的“+1”是因为sigmoid算一次连接
Subsampling2中每个特征图的大小是Conv1中特征图大小的1/4。

4、Conv3

输入：Subsampling2中所有6个或者几个特征图组合
卷积核大小：5*5
卷积核数量：16
输出特征图大小：10*10
于Conv1的区别：Conv3中的每个特征图是连接到Subsampling2中的所有6个或者几个特征图的，表示本层的特征图是上一层提取到的特征图的不同组合。存在方式是：①6个特征图以Subsampling2中3个相邻的特征图子集作为输入。②6个特征图以Subsampling2中4个相邻特征图子集为输入。③3个特征图以不相邻的4个特征图子集作为输入。④1个特征图将Subsampling2中所有特征图作为输入。输出的16个通道并没有与输入的每个通道相连。
在目前流行的卷积神经网络中，已较少使用这样的结构，这样设计的初衷有两个：

有利于提取多种组合特征，希望能检测到不同的模式
降低计算量

可训练参数：6x(3x5x5+1)+6x(4x5x5+1)+3x(4x5x5+1)+1x(6x5x5+1)
连接数：10x10x[6x(3x5x5+1)+6x(4x5x5+1)+3x(4x5x5+1)+1x(6x5x5+1)]=151600

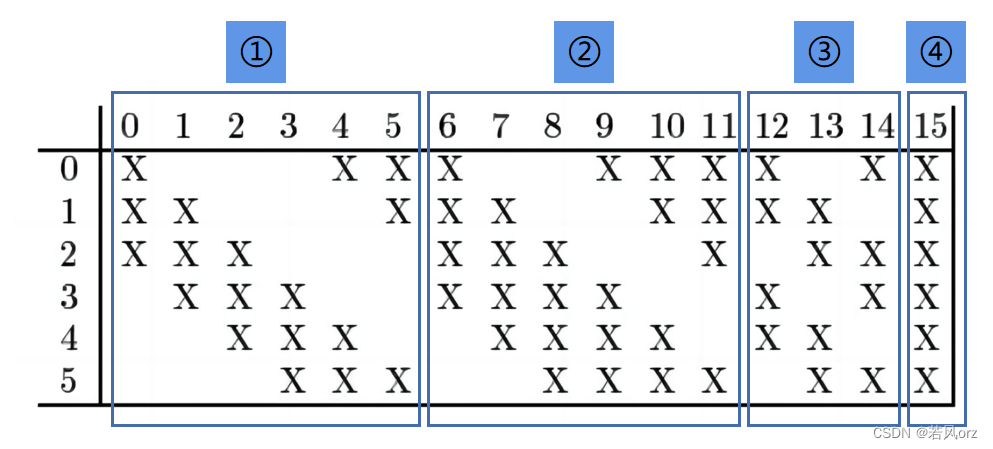
Conv3的前6个特征图（对应上图的①）与Subsampling2层相连的连续3个特征图相连接，后面6个特征图（对应上图的②）与Subsampling2层相连的连续4个相连接，再后面3个特征图（对应上图的③）与Subsampling2层部分不连续的4个特征图相连接，最后1个特征图（对应上图的④）与Subsampling2层的所有特征图相连。

5、Subsampling4

输入：10x10
采样区域大小：2x2
采样方式：与Subsampling2保持一致。4个输入相加，乘以一个可训练参数，再加上一个可训练偏置，结果通过sigmoid函数，步长为2。
采样种类：16
输出特征图大小：5x5
神经元数量：5x5x16
连接数：(2x2+1)x5x5x16=2000
S4中每个特征图的大小是Conv3特征图大小的1/4。

6、Conv5

输入：5x5，即使用Subsampling4的全部16个通道作为输入
卷积核大小：5x5
卷积核数量：120
输出特征图大小：1x1
可训练参数：120x(16x5x5+1)
连接数：(5x5x16+1)x120=48120

7、FC6

输入：120维向量
输出：84维向量
可训练参数：84x(120+1)=10164
计算方式：计算输入向量和权重向量之间的点积，再加上一个偏置，结果通过sigmoid函数输出

8、Output7

输入：84维向量
输出：10维向量
可训练参数：84x10=840
输出共有10个节点，分别代表数字0到9，如果节点i的输出值越接近为0，则网络识别的结果是数字i的可能性越高。这里采用的是欧式径向基函数（Euclidean Radial Basis Function，RBF）的网络连接方式，yi越接近于0，则标明输入越接近于i的比特图编码，本质上是比较"网络处理得到的数字比特图"与"真实比特图"之间的相似度。不过目前RBF已普遍用Softmax代替，RBF了解即可。RBF的计算方式为：

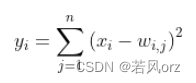
以上是LeNet-5的卷积神经网络的完整结构及详细介绍，整个网络共有60840个训练参数，340908个连接。

五、LeNet-5总结

卷积网络在本质上是一种输入到输出的映射，它能够学习大量的输入与输出之间的映射关系，在神经网络中自动提取图片特征。相比于传统机器学习分类方法，LeNet-5在图片分类上取得了重大突破，为卷积神经网络的后续发展奠定了非常好的基础。LeNet-5作为深度学习入门必学的网络，我们可以通过LeNet-5直观地了解一个卷积神经网络的构建方法，从而掌握对卷积神经网络的整体印象，从而为后续学习、分析、构建更复杂、更多层的卷积神经网络做准备。LeNet-5也有较为明显的弊端，如输入图像太小，只有32x32，数据量不够，数据集小且简单，对于复杂问题的处理结果并不理想，在早期并没有在除手写数字识别之外的其他计算机视觉任务上取得大的突破。且LeNet-5中使用的激活函数，池化方式，及最后输出层和损失函数的设置，都有更好的方法可以代替。