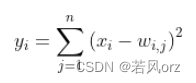加粗样式@LeNet5模型讲解

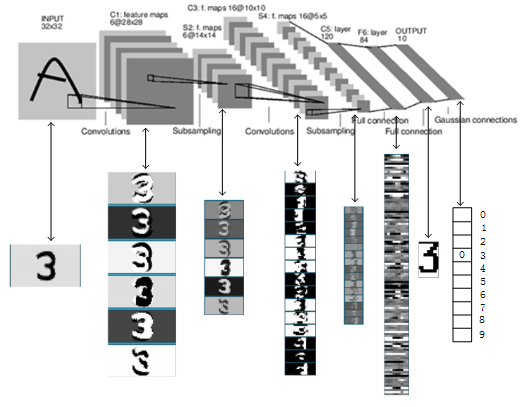
LeNet5模型总览

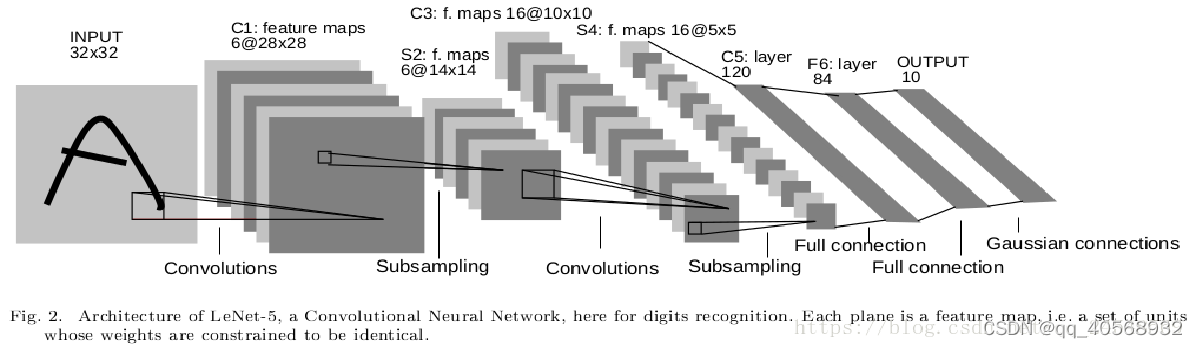
LeNet5模型图
总共8层网络，分别为：
输入层（INPUT）、卷积层（Convolutions,C1）、池化层（Subsampling，S2）、卷积层（C3）、池化层（Subsampling，S4）、卷积层（C5）、全连接层（F6）、输出层（径向基层）。

每层模型讲解

1.输入层（INPUT）：
输入的手写体是32×32像素的图片，论文中说输入像素的背景层(白色)的corresp值为-0.1，前景层(黑色)的corresp值为 1.175，使得平均输入大约为0，方差大约为1，从而加速了学习，要求手写体应该在中心，即20×20以内。

2.卷积层（Convolutions,C1）：提取特征
从LeNet5模型图中可以看出有6个特征平面（通过卷积核提取特征的结果叫特征平面），得到的每个特征平面使用的是一个5×5的卷积核，窗口滑动的权值就是卷积核的内容，特征平面有6个，说明有6个不同的卷积核，因此每个特征平面所使用的权值都是一样的，这样就得到了特征平面。那么特征平面有多少神经元呢？32×32通过一个5×5的卷积核运算，根据局部连接和平滑，需要每次移动1，因此从左移动到右时是28，因此特征平面是28×28的，即每个特征平面有28×28个神经元。6个特征平面对应6个不同的卷积核或者6个滤波器，每个滤波器的参数值也就是权值都是一样的。
该层总共有多少个连接，有多少个待训练的权值呢？
连接数：首先每个卷积核是5×5的，每个特征平面有28×28的神经元（每个神经元对应一个偏置值），总共有6个特征平面，因此连接数为：(5×5+1)×28×28×6 = 122304(+1表示加上一个偏差bias)。权值数：首先，每个特征平面神经元共用一套权值，而每套权值取决于卷积核的大小，因此权值数为：（5×5+1)×6 = 156个。

3.池化层（Subsampling，S2）：降低数据维度
池化层又叫下采样层，目的是压缩数据，降低数据维度，它和卷积有明显的区别，这里采用2×2的选择框进行压缩，通过选择框的数据求和再取平均值然后在乘上一个权值和加上一个偏置值，组成一个新的图片，每个特征平面采样的权值和偏置值都是一样的，因此每个特征平面对应的采样层只有两个待训练的参数。4×4的图片经过采样后还剩2×2，直接压缩了4倍。池化层具有激活函数，为sigmod函数，而卷积层没有激活函数。

4.卷积层（C3）：
这一层也是卷积层，和C2不同的是这一层有16个特征平面，每个特征平面对应的卷积核，和池化层的多个平面进行卷积。把C3的卷积层特征平面编号即0,1,2，…,15，把池化层S2编号为0,1,2,3,4,5。如图1所示：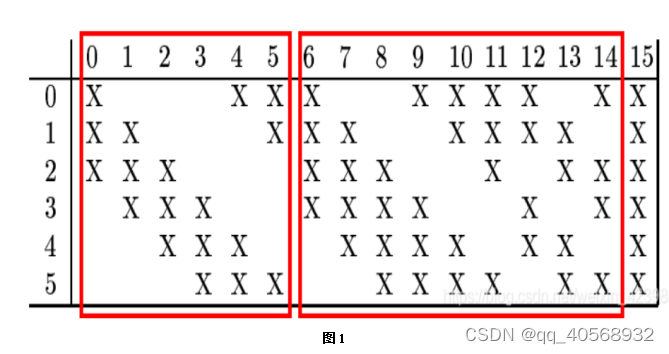
C3层和S2层的对应关系和前面不一样，主要体现在C3的每一个特征平面是对应多个池化层的采样数据，如上图，横向的数表示卷积层C3的特征平面，纵向表示池化层的6个采样平面，我们以卷积层C3的第0号特征平面为例，它对应了池化层的前三个采样平面即0,1,2，三个平面使用的是三个卷积核（每个采样平面是卷积核相同，权值相等，大小为5×5）,对应三个池化层平面，就是说有5×5×3个连接到卷积层特征平面的一个神经元，因为池化层所有的样本均为14×14的，而卷积窗口为5×5的，因此卷积特征平面为10×10，它不是所有的都是特征平面对应三个池化层平面，而是变化的，从上图可以清楚的看到前6个特征平面对应池化层的三个平面即0,1,2,3,4,5，而6-14每张特征平面对应4个卷积层，此时每个特征平面的一个神经元的连接数为5×5×4，最后一个特征平面是对应池化层所有的样本平面，这里大家好好理解。我们来计算一下连接数和待训练权值个数：
连接数：(5×5×3+1) ×10×10×6+(5×5×4+1) ×10×10×9+(5×5×6+1) ×10×10=45600+90900+15100=151600
权值数：(5×5×3+1)×6+(5×5×4+1)×9+5×5×6+1=456+909+151=1516
为什么不和前面的一样进行卷积呢？这里主要是为了打破对称性，提取深层特征，因为特征不是对称的，因此需要打破这种对称，以提取到更重要的特征。

5.池化层（S4）：
这一层采样和前面的采样是一样的，使用的采样窗口为2×2的，对C3层进行采样，得到16个采样平面，此时的采样平面为5×5的，本层存在激活函数，为sigmod函数。

6.卷积层（C5）：
这一层还是卷积层，且这一层的特征平面有120个，每个特征平面是5×5的，而上一层的池化层S2只有16个平面且每个平面为5×5，本层使用的卷积核为5×5，因此和池化层正好匹配，这里每个特征平面连接池化层的所有的采样层，每个卷积核只对应一个神经元，因此本层只有120个神经元并列排列，每个神经元连接池化层的所有层。C5层的每个神经元的连接数为5×5×16+1，因此总共的连接数为：（5×5×16+1)×120=48120,而这一层的权值和连接数一样，因此也有48120个待训练权值。
7.全连接层（F6）：
这一层其实就是BP网络的隐层，为全连接层，即这一层有84个神经元，每一个神经元都和上一次的120个神经元相连接，那么连接数为(120+1)×84=10164,因为权值不共享，隐层权值数也是10164，本层的输出有激活函数，激活函数为双曲正切函数公式
$f (a) = A t a n h (S a)$
根据论文解释：A是幅值，S是原点处的倾斜率，A的经验值是1.7159。输出层：该层有十个神经元，可以理解这是对于手写体10个数，哪个输出的数大，哪个神经元代表的数字就是输出，它不在是BP的神经输出层，而是基于径向基神经网络的输出层，这里使用的是更简单的欧几里得径向基函数。
径向基神经网络是基于距离衡量两个数据的相近程度的，RBF网最显著的特点是隐节点采用输入模式与中心向量的距离（如欧氏距离）。作为函数的自变量，并使用径向基函数作为激活函数。径向基函数关于N维空间的一个中心点具有径向对称性，而且神经元的输入离该中心点越远，神经元的激活程度就越低。上式是基于欧几里得距离，怎么理解那个式子呢？就是说F6层为84个输入用表示，而输出有10个用表示，而权值使用，上式说明所有输入和权值的距离平方和为依据判断，相近距离越小，输出越小则就去哪个，如果我们存储得到的值为标准的输出，如标准的手写体0,1,2,3等，那么最后一层就说明F6层和标准的作比较，和标准的那个图形越相似就说明就越是那个字符的可能性更大。这里的标准字符如图2所示：

这里标准的每个字符都是像素都是12×7=84。这就是解释了为什么F6层的神经元为84个，因为它要把所有像素点和标准的比较在进行判断，因此从这里也可以看出，这里不仅仅可以训练手写体数字，也可以识别其他字符，取决于网络的设计。例如我们让它识别可打印的ASCII码，把小图片添加到这里，同时增加输出的神经元个数就可以完成了。

模型代码(net)

根据LeNet5图搭建网络
import torch
from torch import nn
import torch.nn.functional as F# 定义一个网络模型
class MyLeNet5(nn.Module):# 初始化网络def __init__(self):super(MyLeNet5, self).__init__()# 输入1层，输出6层，卷积核5*5。N=(W-F+2P)/S+1。N：输出大小是28*28，# W：输入大小实际是28*28，F:卷积核大小5*5，S:步长大小1，P：填充值大小2# 定义卷积层c1# self.c1 = nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5, padding=2)self.c1 = nn.Conv2d(in_channels=1, out_channels=6, kernel_size=6, padding=2)# 激活函数self.Sigmoid = nn.Sigmoid()self.ReLU = nn.ReLU()# 使用平均池化定义一个池化层s2，卷积核为2*2,步长也为2self.s2 = nn.AvgPool2d(kernel_size=2, stride=2)# 定义一个卷积层c3,输入为6,输出为16,卷积核5*5# self.c3 = nn.Conv2d(in_channels=6, out_channels=16, kernel_size=5)self.c3 = nn.Conv2d(in_channels=6, out_channels=16, kernel_size=5)# 定义一个池化层s4，卷积核为2*2,步长也为2self.s4 = nn.AvgPool2d(kernel_size=2, stride=2)# 定义一个卷积层c5,输入为16,输出为120,卷积核5*5# self.c5 = nn.Conv2d(in_channels=16, out_channels=120, kernel_size=5)self.c5 = nn.Conv2d(in_channels=16, out_channels=120, kernel_size=4)# 设置一个频展层，因为图片执行到这里是1×1的形式，所以设置一个频展层将其展开。self.flatten = nn.Flatten()# 设置一个全连接层f6,输入120，输出84self.f6 = nn.Linear(120, 84)# 设置输出层output,输入84，输出10self.output = nn.Linear(84, 10)# 传播网络，定义函数forwarddef forward(self, x):# 池化层S2和S4的激活函数是sigmoid函数x = self.Sigmoid(self.c1(x))# x = self.ReLU(self.c1(x))x = self.s2(x)x = self.Sigmoid(self.c3(x))# x = self.ReLU(self.c3(x))x = self.s4(x)x = self.c5(x)x = self.flatten(x)x = self.f6(x)x = self.output(x)return xif __name__ == "__main__":# 随机产生一个张量x = torch.rand([1, 1, 28, 28])# 网络实例化model = MyLeNet5()y = model(x)

训练代码(train)

# 训练函数
import torch
from torch import nn
from net import MyLeNet5
from torch.optim import lr_scheduler
from torchvision import datasets, transforms
import os# 数据转化为tensor格式，原本为矩阵格式
data_transform = transforms.Compose([transforms.ToTensor()
])# 加载训练数据集
train_dataset = datasets.MNIST(root='path', train=True, transform=data_transform, download=True)# 整合格式
train_dataloader = torch.utils.data.DataLoader(dataset=train_dataset, batch_size=16, shuffle=True)
# 加载测试数据集
test_dataset = datasets.MNIST(root='path', train=False, transform=data_transform, download=True)
test_dataloader = torch.utils.data.DataLoader(dataset=test_dataset, batch_size=16, shuffle=True)# 如果有显卡，可以转到GPU
device = "cuda" if torch.cuda.is_available() else 'cpu'
# 调用net里面定义的模型，将模型数据转到GPU上
model = MyLeNet5().to(device)# 定义一个损失函数(交叉熵损失)
loss_fn = nn.CrossEntropyLoss()# 定义一个优化器
optimizer = torch.optim.SGD(model.parameters(), lr=1e-3, momentum=0.9)# 学习率每隔10轮，变为原来的0.1。训练过程越来越大时，防止抖动过大，找不到最低点
lr_scheduler = lr_scheduler.StepLR(optimizer, step_size=10, gamma=0.1)# 定义训练函数
def train(dataloader, model, loss_fn, optimizer):loss, current, n =0.0, 0.0, 0for batch, (X, y) in enumerate(dataloader):# 前向传播X, y = X.to(device), y.to(device)output = model(X)cur_loss = loss_fn(output, y)   # 损失函数_, pred = torch.max(output, axis=1)    # 输出每行最大的概率cur_acc =torch.sum(y == pred)/output.shape[0]# 优化器梯度清零optimizer.zero_grad()# 反向传播cur_loss.backward()optimizer.step()    # 梯度更新loss += cur_loss.item()current += cur_acc.item()n = n + 1print("train_loss" + str(loss / n))print("train_acc" + str(current / n))# 定义一个验证函数
def val(dataloader, model, loss_fn):model.eval()loss, current, n = 0.0, 0.0, 0#在模型不自动更新的情况下自主测试with torch.no_grad():for batch, (X, y) in enumerate(dataloader):# 前向传播X, y = X.to(device), y.to(device)output = model(X)cur_loss = loss_fn(output, y)  # 损失函数_, pred = torch.max(output, axis=1)  # 输出每行最大的概率cur_acc = torch.sum(y == pred) / output.shape[0]loss += cur_loss.item()current += cur_acc.item()n = n + 1print("val_loss" + str(loss / n))print("val_acc" + str(current / n))return current/n    # 返回一个精确度
# 开始训练
epoch = 50
min_acc = 0
for t in range(epoch):print(f'epoch{t+1}\n---------------')train(train_dataloader, model, loss_fn, optimizer)a = val(test_dataloader, model, loss_fn)    #精确度传给a# 保存最好的模型权重if a > min_acc:folder = 'sava_model'if not os.path.exists(folder):os.mkdir('sava_model')min_acc = aprint('save best model')torch.save(model.state_dict(), 'sava_model/best_model.pth')
print('Done!')

测试代码(test)

# 测试函数
import torch
from net import MyLeNet5
from torch.autograd import Variable
from torchvision import datasets, transforms
from torchvision.transforms import ToPILImage# 数据转化为tensor格式，原本为矩阵格式
data_transform = transforms.Compose([transforms.ToTensor()
])# 加载训练数据集
train_dataset = datasets.MNIST(root='path', train=True, transform=data_transform, download=True)# 整合格式
train_dataloader = torch.utils.data.DataLoader(dataset=train_dataset, batch_size=16, shuffle=True)
# 加载测试数据集
test_dataset = datasets.MNIST(root='path', train=False, transform=data_transform, download=True)
test_dataloader = torch.utils.data.DataLoader(dataset=test_dataset, batch_size=16, shuffle=True)# 如果有显卡，可以转到GPU
device = "cuda" if torch.cuda.is_available() else 'cpu'
# 调用net里面定义的模型，将模型数据转到GPU上
model = MyLeNet5().to(device)model.load_state_dict(torch.load("C:/Downloads/Pycharm/pycharm_learn/LeNet_5/sava_model/best_model.pth"))# 获取结果
classes = ["0","1","2","3","4","5","6","7","8","9",
]# 把tensor转化为图片，方便可视化
show = ToPILImage()# 送入验证
for i in range(10):X, y = test_dataset[i][0], test_dataset[i][1]show(X).show()# 张量扩展为4维X = Variable(torch.unsqueeze(X, dim=0).float(), requires_grad=False).to(device)with torch.no_grad():pred = model(X)predicted, actual = classes[torch.argmax(pred[0])], classes[y]print(f'predicted: "{predicted}", actual:"{actual}"')