T检验与方差分析

背景介绍
R语言实操过程--t test
- 单样本t检验
- 两个独立样本t检验
- 配对t检验
R语言实操过程--anova
- 单因素方差分析
- - 多重比较
- 双因素方差分析
完整代码

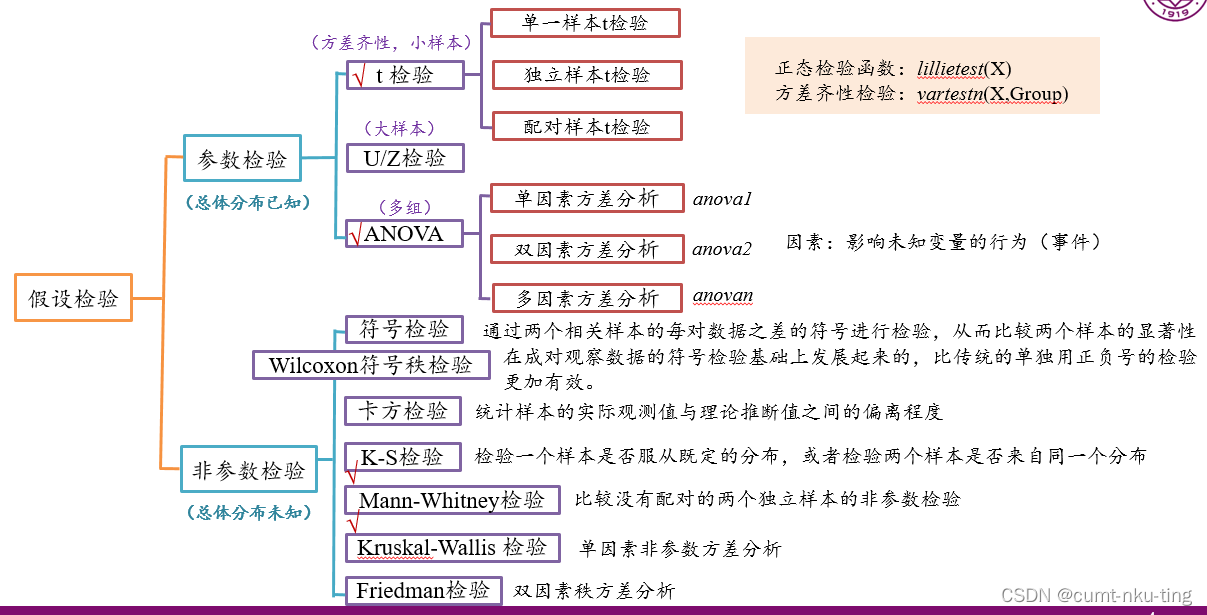
之前与大家分享了数据的独立性、正态性、方差齐性检验。如果还不清楚，大家可以通过这篇推文来学习和理解如何规范你的数据分析？。若满足所有条件，可选择参数分析进行，否则必须选择非参数分析。参数分析主要包括两组样本的t-test ，大于两组的one-way anova以及多重比较。此外，当因子数量大于1时，我们可以使用two-way anova等等。

背景介绍

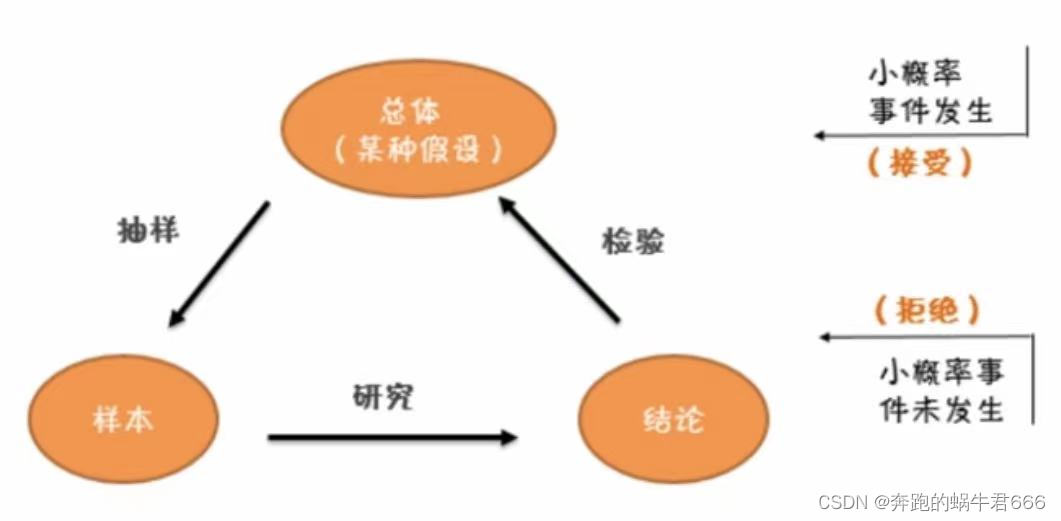
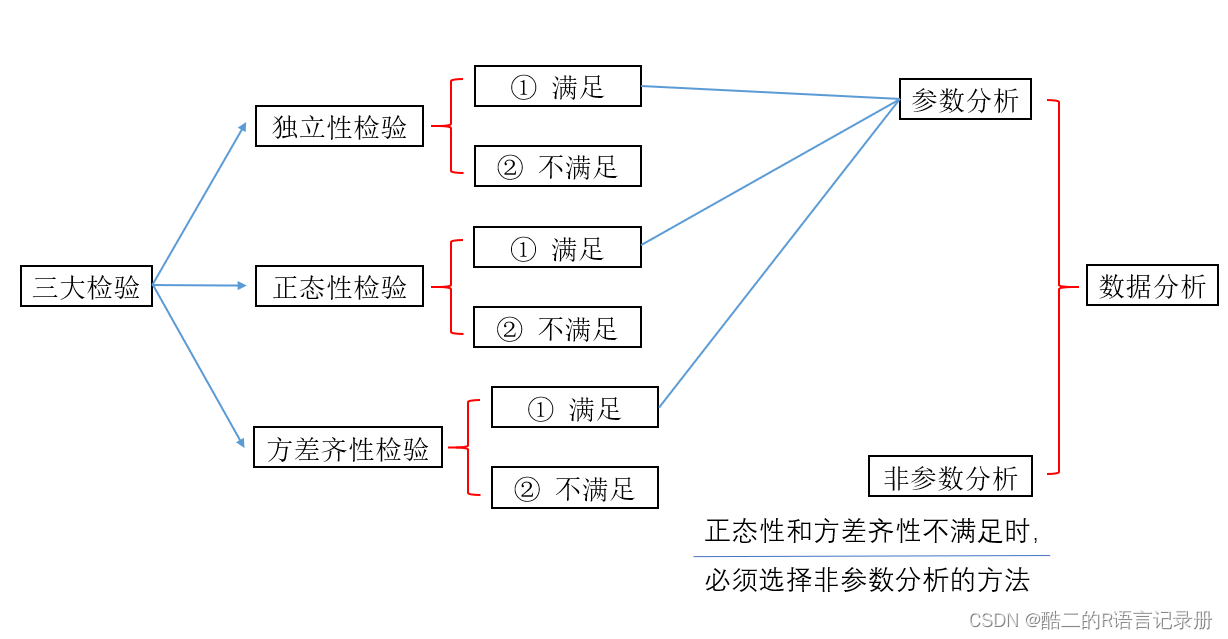
独立性、正态性、方差齐性检验，这三大检验的顺序，以及满足什么条件的时候该用参数与非参数分析。今天，利用下面的流程图做简单介绍：

1）顺序上，三大检验不存在一个孰先孰后的问题。三者都需要做相对应的检验，来判断数据适合用哪种分析方法更科学。

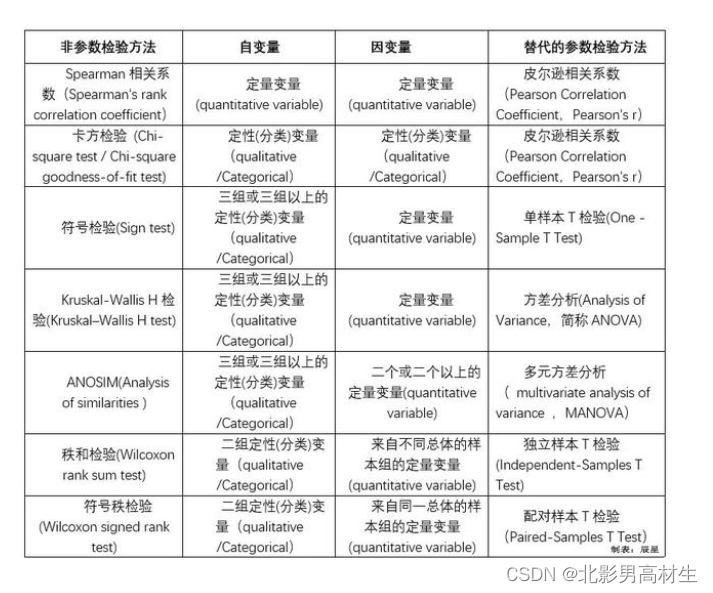
2）条件上，当满足三个条件时，可以选择使用参数分析了。（参数分析有很多种，主要包括t检验、方差分析、Pearson的相关分析等）当正态性与方差齐性都不满足时，必须选择非参数分析，否则统计分析的科学性将大打折扣。（非参数分析主要包括卡方检验、二项分布检验、K-S检验、秩和检验、符号检验、Spearman和Kendall的相关性分析等）

3）具体的原理，这里不做介绍，如果大家对统计学感兴趣的可以自行学习原理介绍。
在这里插入图片描述

R语言实操过程–t test

这里主要分享单样本t检验、两独立样本t检验和配对t检验。主要用到t.test() 函数。

单样本t检验

前提条件

随机样本
样本符合正态分布
方差同质

某全国500强公司的50名经常在上班时偷吃零食，其平均体重为122.8斤，标准差为8.5斤，试分析这些常偷吃零食的员工体重是否不同于专心工作员工的平均值110斤？

由于没有样本，构建符合题目的50个随机样本。

#设置种子数，保重每次结果一致
set.seed (1234)
x <- rnorm(n=50,mean=122.8,sd=8.5) # 生成50个符合正态，均值为122.8，标准差为8.5的样本
hist(x,col="light blue") # 画直方图的基础函数

由于使用生成正态分布的rnorm函数，这里就不做正态性的检验了。
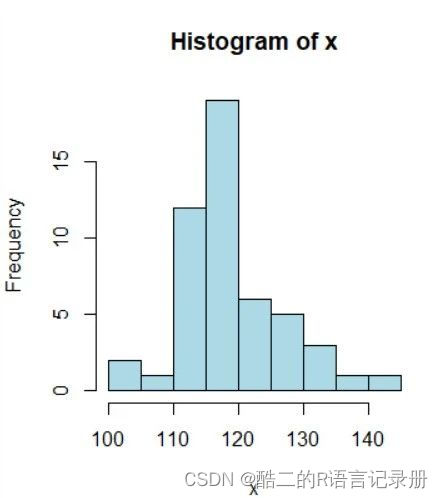
在这里插入图片描述
单一样本，已知总体均值，所以采用单一样本t检验即可50例偷吃零食员工与认真工作的员工的体重是否有差异。

t.test(x,mu=140) # 进行t检验

在这里插入图片描述
以0.05水平为标准，结果为p<0.05，具体统计学意义，表明偷吃与认真的员工体重是存在显著差异。

两个独立样本t检验

前提条件

两个样本应该是相互独立的
样本来自的两个总体应该服从正态分布

根据样本数据对两个样本来自的两个独立总体的均值是否有显著差异进行判断。

使用甲乙两台机床来加工同种零件，两种机床加工零件的尺寸服从正态分布，且方差相同，为检验甲乙两台机床加工的零件尺寸均值是否一致（p=0.05），从两种机床加工的零件中分别抽取若干零件测得的其尺寸如下：

#甲机床加工数据
x1<-c(20.5,19.8,19.7,20.4,20.1,20.0,19.0,19.9)
#乙机床加工数据
x2<-c(20.7,19.8,19.5,20.8,20.4,19.6,20.2)
#进行两样本t检验，指定方差相等
t.test(x1,x2,var.equal=T)

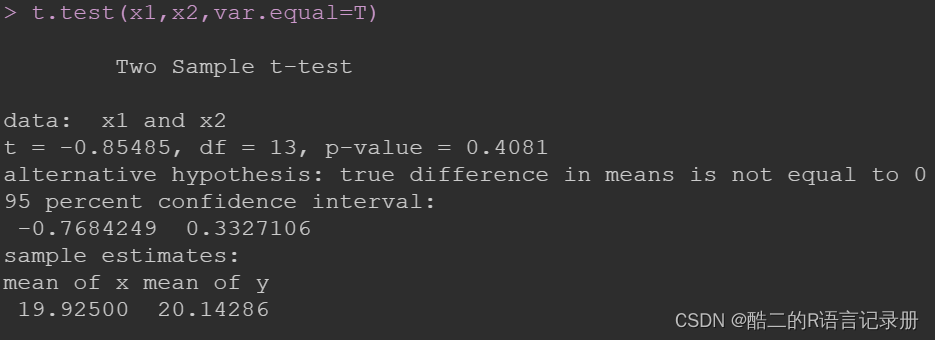
在这里插入图片描述
从结果来看，p=0.4081>0.05，则不能拒绝原假设，即认为两台机床加工零件的尺寸均值没有显著性区别。同时结果也给出了两台机床加工零件尺寸样本数据的均值分别为：19.925和20.14286。

配对t检验

前提条件

两样本必须是配对的.这里有两层意思,即一是两样本的观察值数目相同,两样本的观察值的顺序不随意更改
样本来自的两个总体必须服从正态分布

配对设计主要有4种情况：同一受试对象处理前后的数据，同一受试对象两个部位的数据，同一样品用两种方法检验的结果，配对的两个受试对象分别接受两种处理后的数据。

判断简便法和常规法测定尿铅含量的差别有无统计意义，对12份人尿同时用两种方法进行测定，所得结果如下表所示，请分析两种测定方法的测量结果是否不同？

#读取两组样本的数据
x <- c(2.41,2.90,2.75,2.23,3.67,4.49,5.16,5.45,2.06,1.64,1.06,0.77)
y <- c(2.80,3.04,1.88,3.43,3.81,4.00,4.44,5.41,1.24,1.83,1.45,0.92)
#配对样本t检验
t.test(x,y,paired=T) # paired=T 表示执行配对t检验

在这里插入图片描述
配对t检验的结果为：p=0.874>0.05，不能拒绝原假设H0，显然两种方法测定尿铅含量的结果没有显著差异。

R语言实操过程–anova

在实验设计的时候，通常以单因素或者双因素为主。这里主要分享单因素和双因素方差分析（偶尔用到大于两个因素的实验，方法相同）。主要用到aov() 函数。

方差分析(ANOVA)主要检验不同处理间是否有显著差异，当仅有一个类别型变量(即只有一类处理)，称为单因素方差分析(one-way ANOVA)，当有两个类别型变量(即有两类处理),称为双因素方差分析(two-way ANOVA)，依次类推。单因素方差分析只能告诉处理间是否有显著差异，需要结合多重比较(一般使用TukeyHSD函数)显示哪两种处理水平有显著差异。双因素方差分析能告诉两类处理对响应变量是否有显著影响和交互影响，若无交互作用，两因素方差分析结果近似于分开做两次单因素方差分析，即只考虑两类处理的差异，可以只做单因素方差分析（可能误差很大），若有交互作用，必须做双因素方差分析显示其交互作用。

单因素方差分析

前提条件

样本独立性
样本总体必须服从正态分布
方差齐性

选择R自带的数据集PlantGrowth，研究两个处理和一个对照组对植物产量的影响，每组10例共3记录，主要考察处理对提高植物产量有无影响。
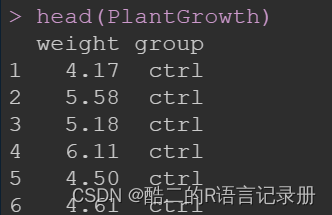
在这里插入图片描述
数据构成：因变量weight，因子变量group，三个水平依次为ctrl、trt1、trt2。

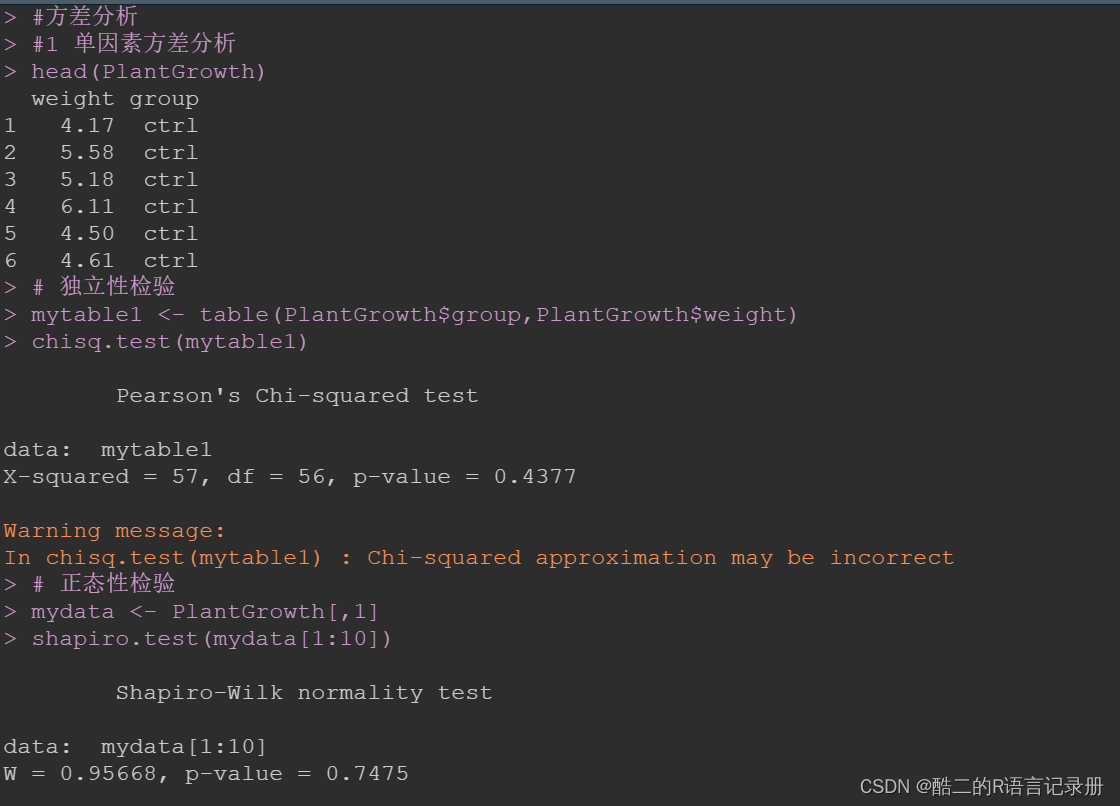
常规的数据分析顺序，先进行三大检验（复习上期内容）。通常我用以下三个函数进行数据的检验，chisq.test-独立性检验、shapiro.test-正态性、bartlett.test-方差齐性。

#1 单因素方差分析
head(PlantGrowth)
# 独立性检验
mytable1 <- table(PlantGrowth$group,PlantGrowth$weight)
chisq.test(mytable1)
# 正态性检验
mydata <- PlantGrowth[,1]
shapiro.test(mydata[1:10]) # 对应group 每组水平下的检验
shapiro.test(mydata[11:20])
shapiro.test(mydata[21:30])
# 方差齐性
bartlett.test(weight~group,data = PlantGrowth)

从三大检验的结果来看，p值均>0.05，也就是都接受了原假设，满足条件。
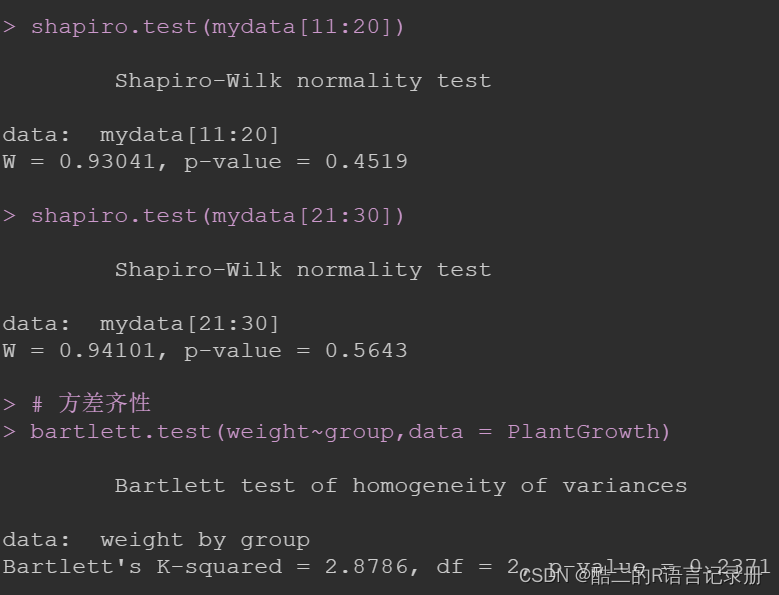
在这里插入图片描述

单因素方差分析

ANOVA <- aov(weight~group,data = PlantGrowth)# weight 因变量在~的左边，group 自变量/处理在~右边
summary(ANOVA)

方差分析表的p=0.0159<0.05，拒绝原假设（H0：3组样本数据均值相等，无差异），说明3组样本均值有差异，不同处理方式对植物产量有显著影响。
在这里插入图片描述
特别注意：对于方差不齐的情况，我们可以尝试用一下oneway.test()函数。

oneway.test(weight~group,data = PlantGrowth,var.equal = F)# “var.equal = F” 表示两样本方差不同（缺省状态，默认状态），“var.equal = T”表示方差相同#

由于前面检验了方差齐性，是相当的。因此，这里结果与上面aov的结果相同。
在这里插入图片描述

多重比较

这里介绍两种LSD.test() 和 Duncan() 函数

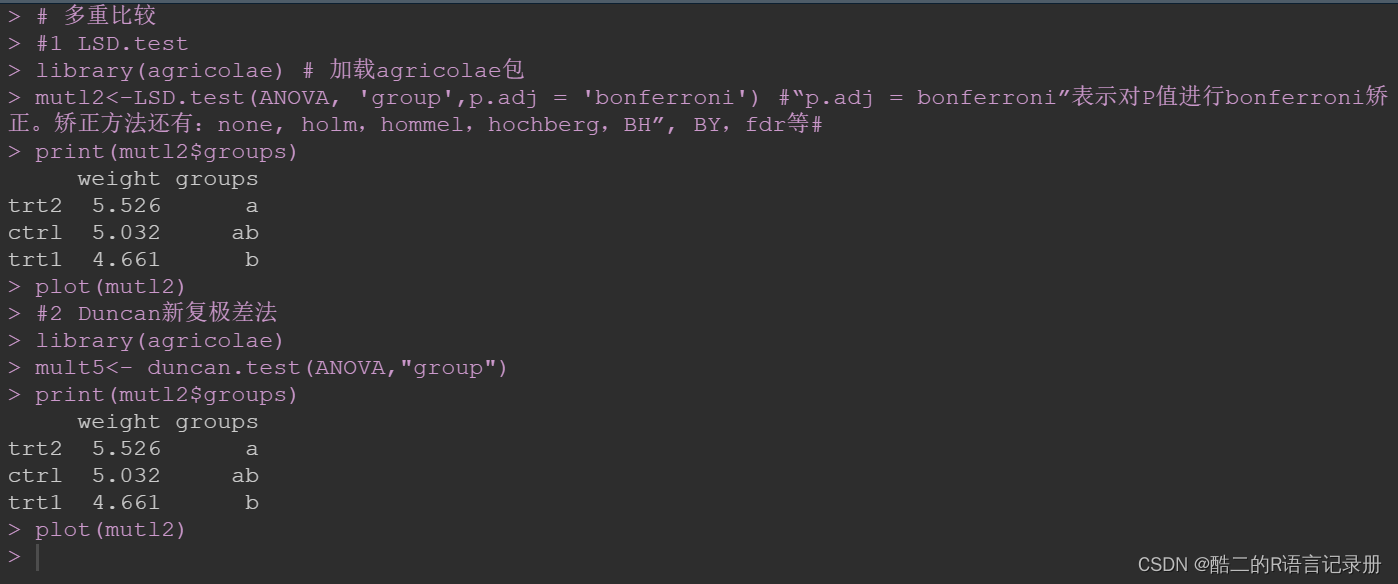
#1 LSD.test
library(agricolae) # 加载agricolae包
mutl2<-LSD.test(ANOVA, 'group',p.adj = 'bonferroni') #“p.adj = bonferroni”表示对P值进行bonferroni矫正。矫正方法还有：none, holm，hommel，hochberg，BH”, BY，fdr等#
print(mutl2$groups)
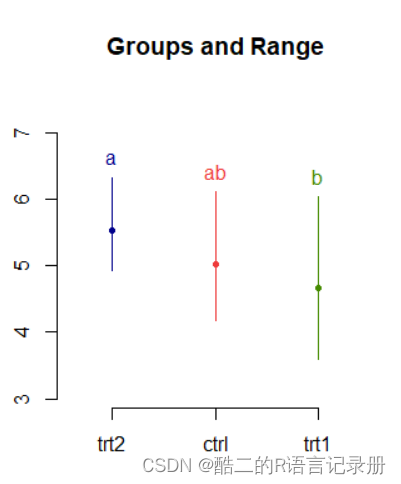
plot(mutl2)#2 Duncan新复极差法
library(agricolae)
mult5<- duncan.test(ANOVA,"group")
print(mutl2$groups)
plot(mutl2)

这两种能够直接展示显著性差异的结果
在这里插入图片描述

双因素方差分析

前提条件与单因素方差一致

双因素方差分析用于检验两个分类变量（自变量）与一个连续变量（因变量）之间的关系。

比方说，如果一个分类变量有两个组别，另外一个分类变量有三个组别，那么一共就有2×3（ = 6）个组别。这里主要介绍样本量相等的情况。

利用R自带的“ToothGrowth”数据集，是研究维生素C对于豚鼠牙齿生长的影响。研究一共包含60只豚鼠，每只豚鼠通过两种给药方式（supp: OJ与VC）给予三种不同剂量的维生素C（dose: 0.5, 1, 2 mg/day）。

# 双因素方差分析
head(ToothGrowth)
summary(ToothGrowth) # 查看数据集的总体情况
str(ToothGrowth) # 查看数据结构

从上述可知，此数据集包含60行*3列的数据。
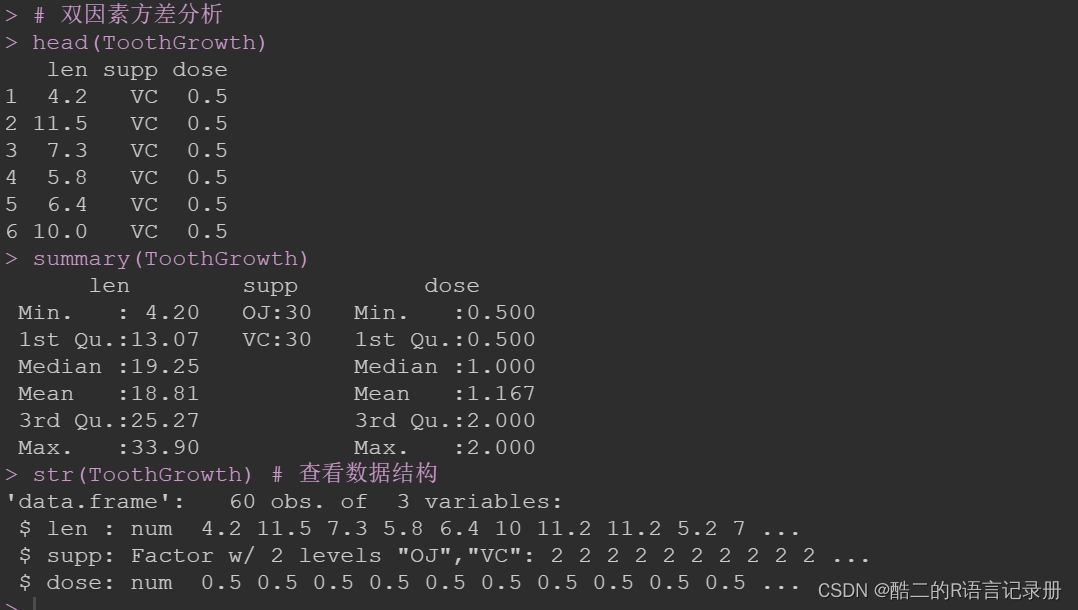
在这里插入图片描述
其中，supp是一个两水平（2 levels）的分类变量（factor）；变量dose在R中是以数值型（num）变量的形式保存。

而双因素方差分析要求两个自变量均为分类变量（categorical variable或factor），所以应将dose转换为factor的形式，以备后续分析使用。

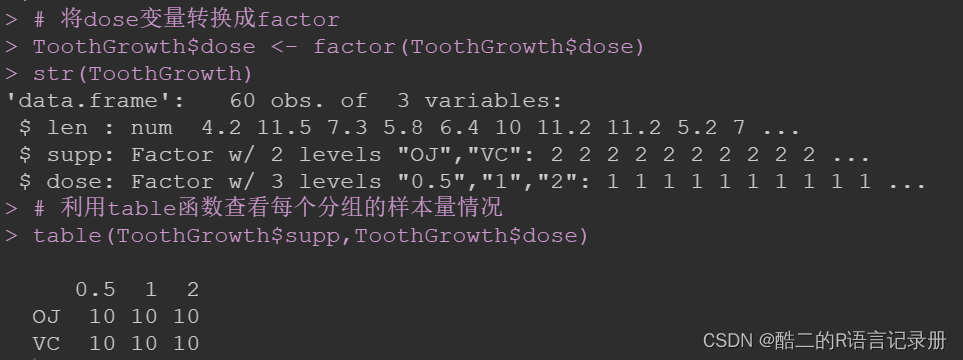
# 将dose变量转换成factor
ToothGrowth$dose <- factor(ToothGrowth$dose)
str(ToothGrowth)
# 利用table函数查看每个分组的样本量情况
table(ToothGrowth$supp,ToothGrowth$dose)

结果可以看出，不同分类变量的样本量是相同的
在这里插入图片描述
简单作图，对样本观测值进行一个初步的描述：

library(ggplot2)
ggplot(ToothGrowth,aes(dose,len,color=supp))+# data=Too... x=dose,y=len,对不同方式进行绘制颜色geom_boxplot() # geom_boxplot 绘制默认的箱线图

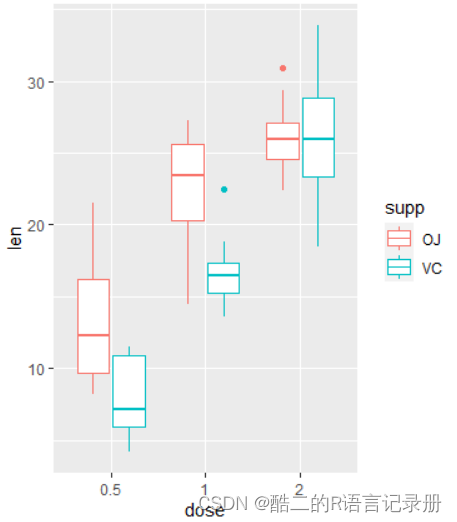
在这里插入图片描述
进一步，通过双因素方差分析来判断不同因子对豚鼠牙齿生长的影响。

# 未包含dose*supp or dose:supp的交互项
anova.1 <- aov(len ~ dose + supp, data = ToothGrowth)
summary(anova.1)

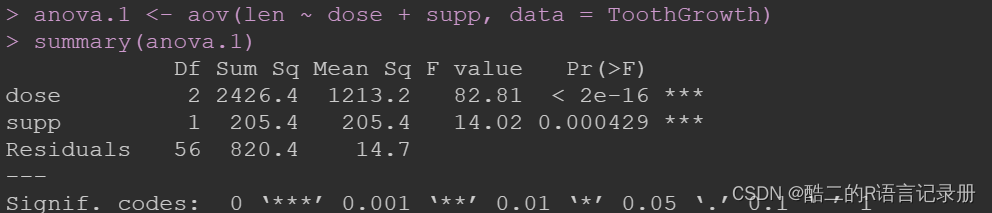
在这里插入图片描述
如果认为dose与supp之间可能存在交互作用；即，想要研究给药剂量（dose）与牙齿生长（len）之间的关系会不会随着给药方式的不同（supp）而改变，则添加交互项。

# 含交互项
anova.2 <- aov(len ~ dose + supp + dose:supp, data = ToothGrowth)
summary(anova.2)
anova.2 <- aov(len ~ dose + supp + dose*supp, data = ToothGrowth)
summary(anova.2)

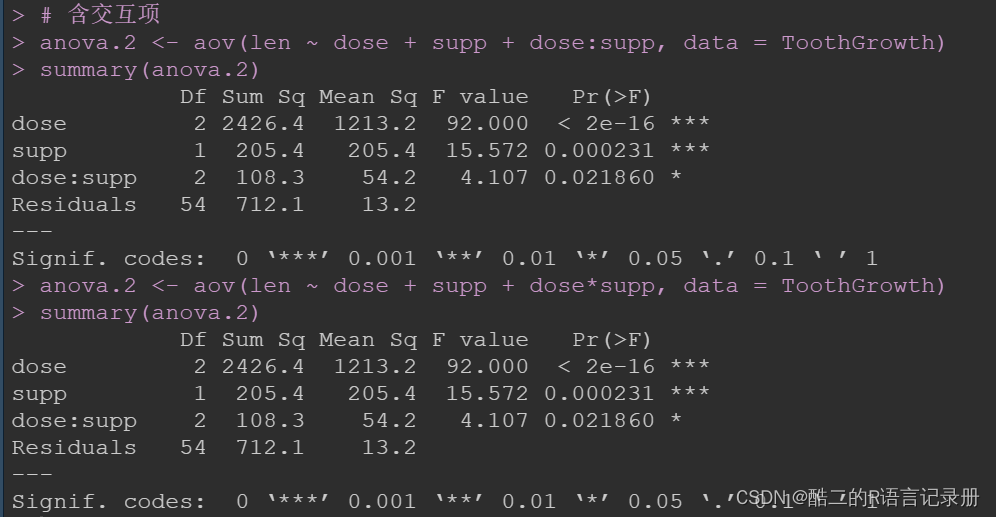
在这里插入图片描述
根据上述结果，将p值设定在0.05水平上，可以得出以下结论：

supp的p值为0.00049，提示不同的给药方式与不同的牙齿长度有关。
dose的p值为<2e-16，提示不同的药物剂量与不同的牙齿长度有关。
（注：上述变量的p值来自anova.1，而不是anova.2）
dose与supp交互项的p值为0.02，提示给药剂量与牙齿长度之间的关系随着给药方式的不同而改变。

完整代码

###########################
# 参数分析之t检验与方差分析
###########################
# t检验
#1 单样本t检验
#设置种子数，保证每次结果一致
set.seed (1234)
x <- rnorm(n=50,mean=122.8,sd=8.5) # 生成50个符合正态，均值为122.8，标准差为8.5的样本
hist(x,col="light blue") # 画直方图的基础函数
t.test(x,mu=140) # 进行t检验#2 两独立样本t检验
#甲机床加工数据
x1<-c(20.5,19.8,19.7,20.4,20.1,20.0,19.0,19.9)
#乙机床加工数据
x2<-c(20.7,19.8,19.5,20.8,20.4,19.6,20.2)
#进行两样本t检验，指定方差相等
t.test(x1,x2,var.equal=T)#3 配对t检验
#读取两组样本的数据
x <- c(2.41,2.90,2.75,2.23,3.67,4.49,5.16,5.45,2.06,1.64,1.06,0.77)
y <- c(2.80,3.04,1.88,3.43,3.81,4.00,4.44,5.41,1.24,1.83,1.45,0.92)
#配对样本t检验
t.test(x,y,paired=T) # paired=T 表示执行配对t检验#方差分析
#1 单因素方差分析
head(PlantGrowth)
# 独立性检验
mytable1 <- table(PlantGrowth$group,PlantGrowth$weight)
chisq.test(mytable1)
# 正态性检验
mydata <- PlantGrowth[,1]
shapiro.test(mydata[1:10])
shapiro.test(mydata[11:20])
shapiro.test(mydata[21:30])
# 方差齐性
bartlett.test(weight~group,data = PlantGrowth)# 单方差分析
ANOVA <- aov(weight~group,data = PlantGrowth)# weight 因变量在~的左边，group 自变量/处理在~右边
summary(ANOVA)
oneway.test(weight~group,data = PlantGrowth,var.equal = F)# “var.equal = F” 表示两样本方差不同（缺省状态，默认状态），“var.equal = T”表示方差相同## 多重比较
#1 LSD.test
library(agricolae) # 加载agricolae包
mutl2<-LSD.test(ANOVA, 'group',p.adj = 'bonferroni') #“p.adj = bonferroni”表示对P值进行bonferroni矫正。矫正方法还有：none, holm，hommel，hochberg，BH”, BY，fdr等#
print(mutl2$groups)
plot(mutl2)#2 Duncan新复极差法
library(agricolae)
mult5<- duncan.test(ANOVA,"group")
print(mutl2$groups)
plot(mutl2)# 双因素方差分析
head(ToothGrowth)
summary(ToothGrowth) # 查看数据集的总体情况
str(ToothGrowth) # 查看数据结构
# 将dose变量转换成factor
ToothGrowth$dose <- factor(ToothGrowth$dose)
str(ToothGrowth)
# 利用table函数查看每个分组的样本量情况
table(ToothGrowth$supp,ToothGrowth$dose)library(ggplot2)
ggplot(ToothGrowth,aes(dose,len,color=supp))+# data=Too... x=dose,y=len,对不同方式进行绘制颜色geom_boxplot() # geom_boxplot 绘制默认的箱线图# 未包含dose*supp or dose:supp的交互项
anova.1 <- aov(len ~ dose + supp, data = ToothGrowth)
summary(anova.1)
# 含交互项
anova.2 <- aov(len ~ dose + supp + dose:supp, data = ToothGrowth)
summary(anova.2)
anova.2 <- aov(len ~ dose + supp + dose*supp, data = ToothGrowth)
summary(anova.2)