目录

一、配对：Wilcoxon符号-秩检验

分析

操作

结果及分析

二、独立样本：Mann-Whitney U检验

分析

操作

结果及分析

三、单因素ANOVA：Kruskal-Wallis检验

分析

操作

结果及分析

---

一、配对：Wilcoxon符号-秩检验

分析：

配对t检验适用于两组差值近似服从正态分布的数据。当不满足该前提时，可选择Wilcoxon符号秩检验。

案例：研究者拟判断同一组研究对象在药物治疗前后体内甘油三酯水平的变化，本研究的数据为非正态分布。针对这种情况，我们可以使用Wilcoxon符号秩检验。

需要满足3项假设：

假设1：观测变量是连续变量或有序分类变量

假设2：研究数据可以被分为两组，如本研究数据可以分为治疗前和治疗后两组。

假设3：数据结构为配对形式，如本研究数据属于研究对象自身配对的形式。

 

建立检验假设，确定检验水准：

H0：差值的总体中位数等于0

H1：差值的总体中位数不等于0

检验水准α=0.05

操作：        

1、评估差值是否正态分布，不是，可用非参数检验

2、连续变量（额外计算中位数）转换-计算变量；分析-比较平均值-平均值

3、分析-非参数检验-旧对话框-2个相关样本

结果及分析：

1、是否正态

2、Wilcoxon符号秩检验显示，Z=-3.928，P<0.001，按检验水准α=0.05，拒绝H0，说明两组数据中位数差值与0的差异具有统计学意义，即治疗前和治疗后研究对象甘油三酯水平中位数不同。结合中位数的结果可知，该药物有助于降低研究对象的甘油三酯水平（P<0.001）。

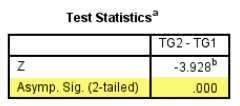
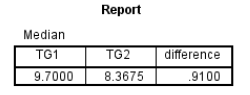
3、连续变量（额外计算中位数），基线时研究对象的甘油三酯水平中位数为9.70mmol/L，药物治疗后研究对象的甘油三酯水平中位数为8.37 mmol/L，差值的中位数位0.9100 mmol/L。

二、独立样本：Mann-Whitney U检验

分析：

当资料不服从正态分布，可选择Mann-Whitney U检验。

案例：某研究者想了解某工作岗位男性和女性的收入差异。该研究者招募20名男性和20名女性，收集了每个研究对象的性别（变量名为gender）和每月平均收入水平（变量名为income）。由于一般情况下收入水平不服从正态分布（仅为模拟数据，实际使用时需要专业判断或结合正态性检验结果），因此可以使用Mann-Whitney U检验。

使用Mann-Whitney U检验时，需要考虑以下3个假设。

假设1：有一个因变量，且因变量为连续变量或等级变量。

假设2：有一个自变量，且自变量为二分类。

假设3：具有相互独立的观测值。

 

建立检验假设，确定检验水准：

H0：两个总体分布位置相同

H1：两个总体分布位置不同

检验水准α=0.05

操作：

1、拆分数据并评估是否符合正态分布

2、连续变量（额外计算中位数）分析-比较平均值-平均值：如果实际研究中，各组因变量的分布形状基本一致，则需要计算并汇报各组因变量的中位数。如果各组因变量的分布形状不一致，则在统计描述时不必汇报

3、分析-非参数检验-旧对话框-2个独立样本

结果及分析：

1. 是否正态
2. Test Statistics表格中Mann-Whitney U代表检验的U统计量值为148.0。

当每个分组的样本量小于20时，SPSS软件计算精确P值，选择精确P值来判断检验假设。当样本量大于20时，选择渐进P值来判断检验假设。

本例中每组的样本量为20个，结果报告了精确P值为【】，本例选用精确P值判断检验假设，P值小于检验水准0.05，因此拒绝原假设H0，即认为男性和女性的收入水平分布有统计学差异。

      3.中位数

三、单因素ANOVA：Kruskal-Wallis检验

分析：

由于CWWS得分不服从正态分布，因此可以使用Kruskal-Wallis检验。Kruskal-Wallis检验是基于秩次的非参数检验方法，用于检验多组间连续或有序分类变量是否存在差异。

使用Kruskal-Wallis检验时，需要考虑以下3个假设。

假设1：有一个因变量，且因变量为连续变量或有序分类变量。

假设2：存在多个分组（≥2个）。

假设3：具有相互独立的观测值。

 

建立检验假设，确定检验水准：

H0：三组【】的总体分布位置相同

H1：三组【】的总体分布位置不全相同

检验水准α=0.05

 

多重比较建立检验假设，确定检验水准：

H0：第i组与第j组所代表的总体中位数相等

H1：第i组与第j组所代表的总体中位数不等

检验水准α=0.05

操作：

1、观察是否服从正态，画直方图  数据-拆分文件（记得合并）

2、连续变量（额外计算中位数）分析-比较平均值-平均值：如果实际研究中，各组因变量的分布形状基本一致，则需要计算并汇报各组因变量的中位数。如果各组因变量的分布形状不一致，则在统计描述时不必汇报

3、分析-非参数检验-独立样本

        

结果及分析：

1. 是否正态
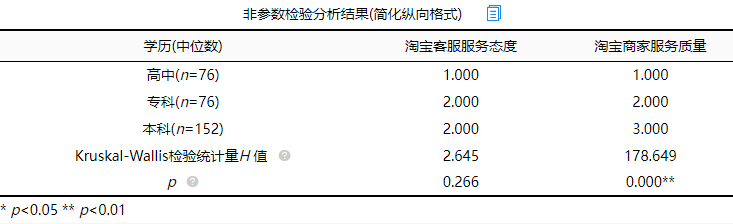
2. 比较不同工作年限人群之间CWWS评分的分布差异，采用Kruskal-Wallis检验。H= 【】，P<0.001，拒绝H0，可以认为各组CWWS评分的分布不全相同，差异具有统计学意义。

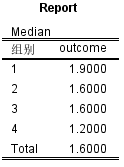
    3.根据直方图判断各组中CWWS评分分布的形状基本一致。工作0-5年CWWS评分中位数为3.82（n=7），6-10年CWWS评分中位数为5.50（n=9），11-15年CWWS评分中位数为6.29（n=8），>16年CWWS评分中位数为7.47（n=7），总的CWWS评分中位数为5.85（n=31）。

   4.事后校正/两两比较：查看-成对比较

SPSS也提供了调整后P值（Adj. Sig.），其思想还是采用Bonferroni法调整α水平。该列是将原始P值（Sig.）乘以比较次数得到，因此可以直接和0.05比较，小于0.05则认为差异有统计学意义。

以上结果可以描述为：采用Bonferroni法校正显著性水平的事后两两比较发现，CWWS评分的分布在【】（调整后P=0.002）、【】（调整后P<0.001）的差异有统计学意义，其它组之间的差异无统计学意义。

 

PS.   参考链接：https://www.mediecogroup.com/zhuanlan/lessons/109/