第4章 Stata参数检验

article/2025/9/15 2:17:35

4.1单一样本T检验

案例延伸

4.2独立样本T检验

案例延伸

1.改变置信水平

2.在异方差假定条件下进行假设检验

4.3配对样本T检验

案例延伸

1.改变置信水平

4.4单一样本方差的假设检验

案例延伸

4.5双样本方差的假设检验

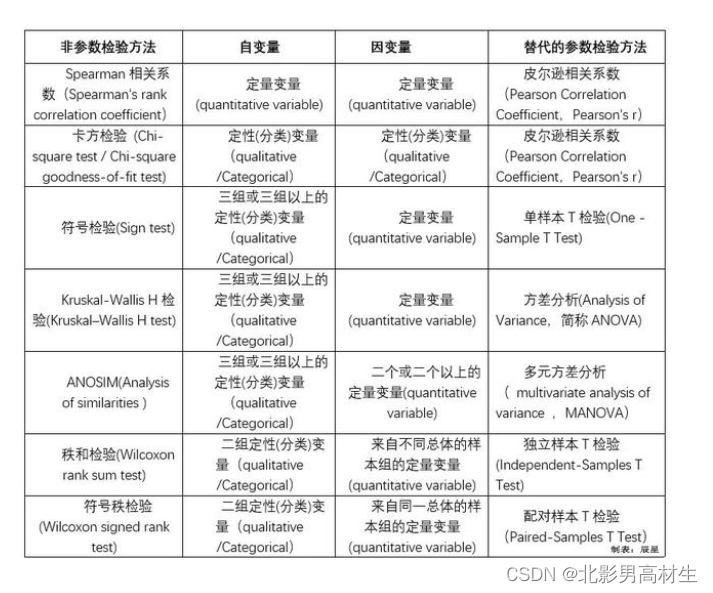
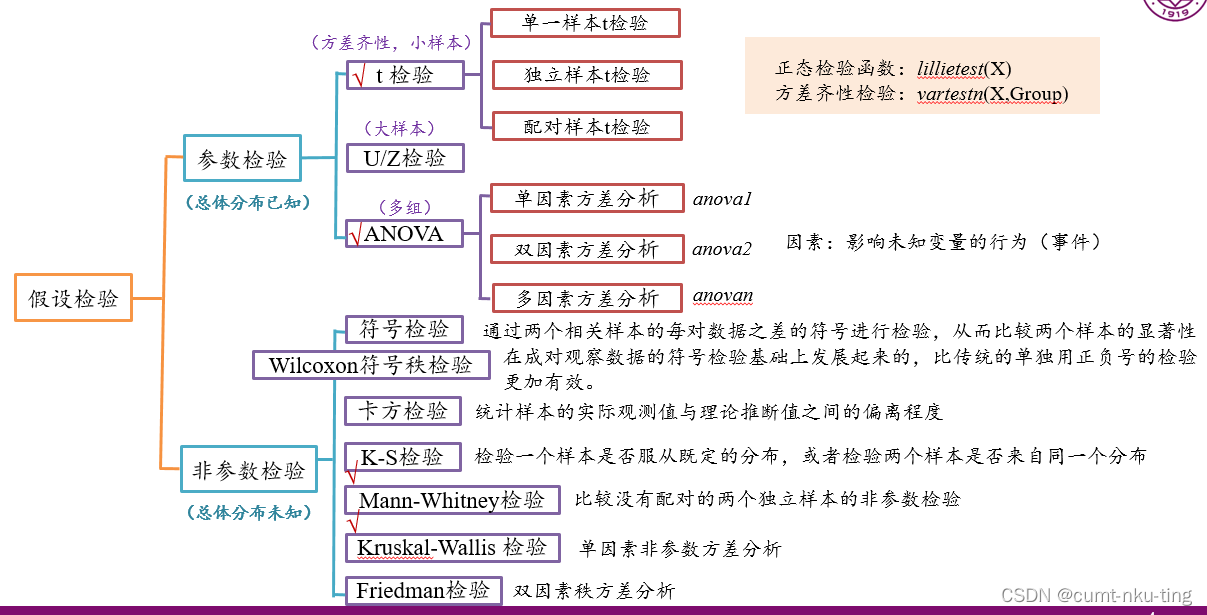
参数检验（Parameter Test）是指对参数的平均值、方差、比率等特征进行的统计检验。参数检验一般假设统计总体的具体分布为已知，但是其中一些参数或者取值范围不确定，分析的主要目的是估计这些未知参数的取值，或者对这些参数进行假设检验。参数检验不仅能够对总体的特征参数进行推断，还能够对两个或多个总体参数进行比较。常用的参数检验包括单一样本T检验、独立样本T检验、配对样本T检验、单一样本方差和双样本方差的假设检验等。

4.1单一样本T检验

单一样本T简单是假设检验中最基本也是最常用的方法之一。与所有的假设检验一样，其依据的基本原理也是统计学中的“最小概率反证法”原理。通过单一样本T检验，我们可以实现样本均值和总体均值的比较。检验的基本程序是首先提出原假设检和备择假设，规定好检验的显著水平，然后确定适当的检验统计量，并计算检验统计量的值。最后依据计算值和临界值的比较结果做出统计决策。

数据（案例4.1）是河南省某高校5年前对大四学生体检时，发现学生的平均体重是67.4KG.最近又抽查测量了该校53名大四学生的体重。试用单一样本T检验的操作命令判断该校大四学生的体重与5年前相比是否有显著差异。

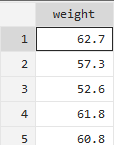
ttest weight=67.4

我们可以看出一共有53个样本参与了假设检验，样本的均值是58.61887、标准误是0.7094891、标准差是5.165159、95%置信度区间是[57.19517 60.04256]。样本的T值是-12.3767、自由度是52，Pr(|T|>|t|)=0.0000,远小于0.05，需要拒绝原假设，也就是说该校大四学生的体重与五年前相比有显著差异。

案例延伸

我们要把显著性水平跳到1%，也就是说置信水平为99%。

ttest weight=67.4，level(99)

从上面得分系结果中可以看出与95%置信水平不同得地方在于置信区间得到了进一步的放大，这是正常的结果，因为这是要取得更高置信水平所必须付出的代价。

4.2独立样本T检验

独立样本T检验也是假设检验中最基本最常用的方法之一。通过独立样本T检验我们可以实现两个独立样本的均值比较。独立样本T检验过程的基本程序也是首先提出原假设和备择假设，规定好检验的显著性水平，然后确定适当的检验统计量，并计算检验统计量的值，最后依据计算值和临界值的比较结果做出统计决策。

数据（案例4.2）给出lAB两所学校各40名高三学生的高考英语成绩。试用独立样本T检验方法研究两所学校被调查的高三学生的高考英语成绩之前有无明显的差异（设定显著性水平为5%）。

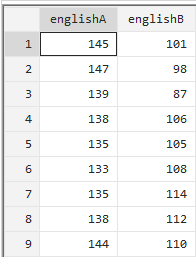
ttest englishA=englishB,unpaired

从上图我们可以看出一共有80个有效样本参与了假设检验，自由度为78，其中变量englishA包括40个样本，均值是135.175，标准差为11.70336，标准误是1.850463，95%的置信区间是[131.4321,138.9197];变量englishB不再过多赘述。Pr（|T|>|t|）=0.0000远小于0.05，需要拒绝原假设，也就是说两个两所学校被调查的高三学生的高考英语成绩之间存在明显的差别。

案例延伸

1.改变置信水平

ttest englishA=englishB,unpaired level(99)

2.在异方差假定条件下进行假设检验

上面的检验过程是假定两个样本代表的总体之间存在相同的方差，如果假定两个样本代表的总体之间的方差并不相同。操纵命令如下

ttest englishA=englishB ,unpaired level(99) unequal

4.3配对样本T检验

通过配对样本T检验，我们可以实现对成对数据的样本均值比较。其与独立样本T检验的区别是；两个样本来自于同一总体，而且数据的顺序不能调换。基本程序也是首先提出原假设和备择假设，规定好检验的显著性水平，然后确定适当的检验统计量，并计算检验统计量的值，最后依据计算值和临界值的比较结果做出统计决策。

数据（案例4.3）为了研究一种减肥药品的效果，特抽取了30名实验者进行检验，服用该产品一个疗程前后的体重在数据中。试用配对样本T检验的方法判断该药物能否引起实验者体重的明显变化（设定显著性水平为5%）。

ttest qian=hou

结果与上述相差无几，最后结论是药物能引起实验者体重的明显变化。

案例延伸

1.改变置信水平

ttest qian=hou,level(99)

4.4单一样本方差的假设检验

方差的概念是用来反应波动情况，常用语质量控制与市场波动等情况。单一总体方差的假设检验的基本程序也是首先提出原假设和备择假设，规定好检验的显著性水平，然后确定适当的检验统计量，并计算检验统计量的值，最后依据计算值和临界值的比较结果做出统计决策。

数据（案例4.4）为研究某只股票的收益波动情况，某课题组对该股票连续60天的收益率情况进行了调查研究。试对该数据进行假设检验其方差是否等于1（设显著性水平为5%）

sdtest return=1

结果如图所示我们可以看到一共有60个样本参与了假设检验，自由度为59，均值为0.2539735，标准差为0.4813014，标准误为0.621357，95%的置信区间是[0.1296402,0.3783069]。2*Pr(C<c)=0.0000,远小于0.05所以拒绝原假设，也就是说该股票的收益率方差不显著等于1。