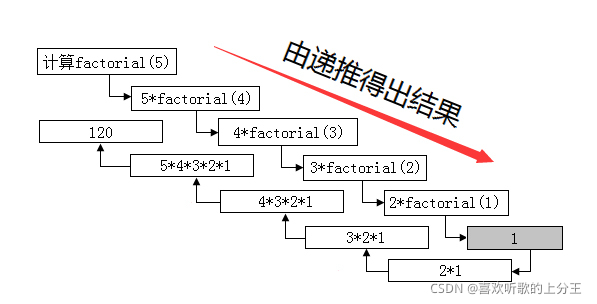
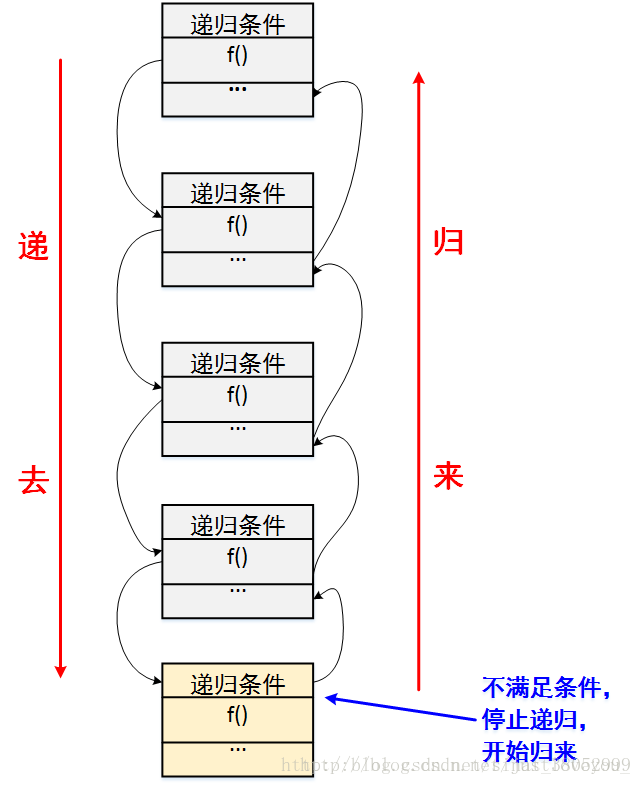
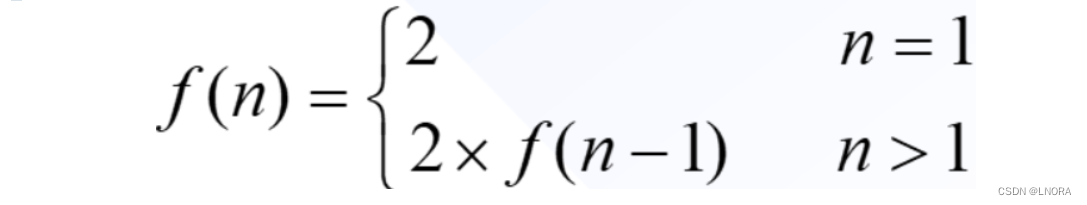递归算法整理合集

​递归是常见的算法和编程思想，也是初学者几乎最早接触的算法思想之一。递归算法的优点是代码简洁清晰，逻辑简单易懂；缺点一是算法运行复杂度较高，二是容易在具体代码实现的时候调用栈的层次考虑不周，导致出现错误。但是如果仅仅想实现一个复杂的问题，而不是很关注复杂度的时候，递归算法无疑是一个很好的选择。(实际上，现有的编译器优化很多已经能够自动将递归代码优化为非递归结构实现，因此，如果实用中开启编译器优化，则大多数递归算法的复杂度其实也可以不必考虑)

​本文对递归算法的一些典型题目和例子做了梳理，代码示例有的是用C++，有的是用python，之所以用不同的语言混杂，纯属是具体例题的方便起见，有些地方使用python而不用C++，只是为了更加方便阅读和理解主要思路，而不是过多地关注底层的代码细节。

例题1：斐波拉契数列

​斐波拉契数列是最容易想到的递归算法典例，但是直接递归复杂度为指数级别，很容易即超出时间限制，如果将每次计算的结果变成数组，其思想还是递归的思想，但更改了一种实现方式，则算法复杂度会降低为O(n)量级，代码如下：

class Solution {
public:int fib(int n) {int a[31]={0,1};for(int i=2;i<31;i++){a[i]=a[i-1]+a[i-2];}return a[n];}
};

例题2:全排列问题

​全排列问题是面试中经常会考察的算法题目，即给出一组不重复的数字，要求输出所有的可能的排列。由基础的组合数学知识，我们可以知道，一共有$n!$种可能的排列，但是如何通过计算机输出呢？

​如果采取递归的思想，容易想到，每个数字作为第一个数字，都会对应$(n-1)!$种排列，即剩下的$(n-1)$个元素的排列数，这样就可以构造递归的结构了，这里用python实现如下：

class Solution:def permute(self, nums: List[int]) -> List[List[int]]:if len(nums)==1:return [nums]if len(nums)==2:return [nums,nums[::-1]]ans = []for a in nums:tmp = copy.deepcopy(nums)# 这里用到deepcopy就是因为python的列表对象直接相等是浅复制，会不对，当然也可以用别的方法去除某元素，比如拼接tmp.remove(a)for i in self.permute(tmp):ans.append([a]+i)return ans

例题3:N皇后问题

​N皇后问题是比较难的递归题目，通常用DFS算法实现，而DFS一般又通过递归实现。

​目前比较简洁和高效的题解是这样的：

​

​首先，我们是逐行扫描的，因此不需要考虑行的重合问题；其次，列的重合问题也比较容易考虑，只需要一个长度为N的数组来进行记录即可；最后，需要考虑的是对角线元素，这里不能头大，只需要观察规律，就可以发现对角线元素的特点。对于每一条对角线而言，都是一条截距固定且斜率绝对值为1的直线，因此，$i+y$的值或者$n-x+y$的值必然是固定的，比如过$(0,1)$和$(1,0)$格子，即构成一个/型对角线，又比如$(0,2)$和$(1,3)$，满足$4-0+2=4-1+3$,因此也在一条\对角线上。这样有什么好处呢？这样的好处就是对角线是否有值了就可以直接一条对角线用一个$a[i+j]$或$a[n-i-j]$来记录了，对应的记录对角线的数组应该多大呢？只需要考虑一下边界就可以了。对于/型对角线，可以知道最大的$i+j=n-1+0=n-1$，最小的$i+j=1+0=1>0$所以只需要长度为$n$的数组就可以了；对于\型对角线，可以知道最大的$n-i+j=n-0+0=n$，最小的$n-(n-1)+0=1+0=1>0$所以也是只需要长度为$n$的数组就可以了。

​下面就可以递归了：

​从第一行开始，每一列进行搜索，然后当前这一列和对应的对角线(四角的元素只有一个，其实无所谓对角线)标记为访问过，即为True，之后，就从第二行开始，如果没有冲突，就继续执行此摆放程序，即深度优先搜索DFS，但行数为下一行，如果有冲突，则continue，不再递归，即停止此路径的搜索，相当于DFS剪枝。需要注意的是，由于递归调用了全局变量，因此，每次递归调用后，需要把函数值恢复为原来的值，这一点比较绕，需要注意！代码如下：

class Solution {
public:vector<vector<string>> solveNQueens(int n) {vector<vector<string>> ans;vector<string>board(n,string(n,'.'));vector<bool> col(n,false); //记录列vector<bool> r(n,false);   //记录正对角线vector<bool> l(n,false);   //记录反对角线backtrace(ans,board,col,l,r,0,n);return ans;}void backtrace(vector<vector<string>> &ans,vector<string> &board,vector<bool>  &col,vector<bool>  &l,vector<bool>  &r,int row,int n){if(row==n){ans.push_back(board);return;}for(int j=0;j<n;j++){if(col[j]||r[j+row]||l[n-j+row])continue;col[j]=r[j+row]=l[n-j+row] = true;board[row][j] = 'Q';backtrace(ans,board,col,l,r,row+1,n);//注意此处要恢复原来的值，保存栈现场col[j]=r[j+row]=l[n-j+row] = false;board[row][j] = '.';}}
};

例题4:岛屿数量问题

​岛屿数量问题也是比较常见的算法题，即给出一个01矩阵，要求其中的闭集数量，即1连成片可以构成一个“岛屿”，要求一共有多少个“岛屿”存在。

​这个就不同于上面的DFS了，这个是找到邻居，标记，邻居的邻居也要标记，因此是广度优先搜索，是BFS问题，通过BFS+递归，可以很漂亮地解决这个问题。具体思路是这样的：

​按行按列遍历矩阵的每一个元素，如果元素是0，那是水域，跳过即可；如果这个元素为1说明为陆地，记录数量+1，这个点置为0，同时对此元素BFS递归，即任何于其相邻的1元素在此时都会被搜索到，搜索到怎么办呢？就是把搜索到的邻域的1都置为0,这样统计数量就很容易了。总体思想就是递归+BFS，还有一点并查集的思想。

​代码实现如下：

class Solution:def numIslands(self, grid: List[List[str]]) -> int:n=len(grid)m=len(grid[0])count=0def dfs(x,y):for i,j in [[x+1,y],[x-1,y],[x,y+1],[x,y-1]]:if 0<=i<n and 0<=j<m and grid[i][j]=='1':# 只有搜索到陆地的时候才操作grid[i][j] = '0'dfs(i,j)for i in range(n):for j in range(m):if grid[i][j]=='1':grid[i][j]='0'dfs(i,j)count+=1return count

例题5:二叉树的前中后序遍历

​二叉树的前中后序遍历问题是典型的递归实现算法，不再多言，如下所示：

struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
//前序遍历
void preorder(TreeNode *root,vector<int>&path){if(root){path.push_back(root->val);preorder(root->left,path);preorder(root->right,path);}
}
//中序遍历
void inorder(TreeNode *root,vector<int>&path){if(root){inorder(root->left,path);path.push_back(root->val);inorder(root->right,path);}
}
//后序遍历
void postorder(TreeNode *root,vector<int>&path){if(root){postorder(root->left,path);postorder(root->right,path);path.push_back(root->val);}
}

例题6:N叉树的后序遍历

N叉树的遍历和二叉树其实没有本质的区别，只不过多了个for循环而已，这里以后序遍历为例，看一下代码实现：

/*
// Definition for a Node.
class Node {
public:int val;vector<Node*> children;Node() {}Node(int _val) {val = _val;}Node(int _val, vector<Node*> _children) {val = _val;children = _children;}
};
*/
class Solution {
public://这里必须要分开两个函数调用，否则一个函数要返回值，无法递归vector<int> postorder(Node* root) {vector<int> ret;dfs(ret,root);return ret;}void dfs(vector<int>& ret,Node* root){if(root){for(int i=0;i<root->children.size();i++)dfs(ret,root->children[i]);ret.push_back(root->val);}}
};

例题7:快速幂算法

​著名的快速幂算法常用来计算大指数，广泛应用于密码学等领域。快速幂算法也应用了递归的基本思想，即每次幂为原来的1/2处理，从而以指数级别降幂运算，其实也是递归的思想，代码如下：

def myPow(x, n):if x == 0.0: return 0.0res = 1if n < 0: x, n = 1 / x, -nif n==0:return 1elif n%2==1:return myPow(x,n-1)*xelse:temp = myPow(x,n//2)return temp ** 2

​当然，平时应用的快速幂算法多是非递归位运算实现，但由于本文主要讲解递归算法，就不在这里详细说明了。

​以上就是梳理的一些经典的递归算法例题，供大家参考。