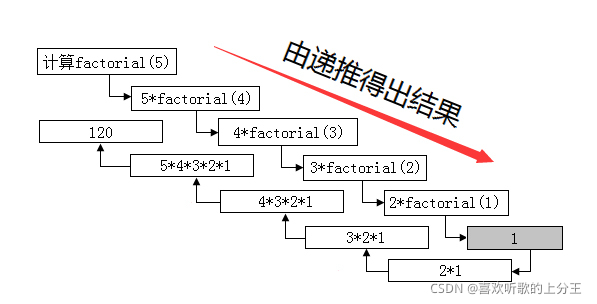
递归

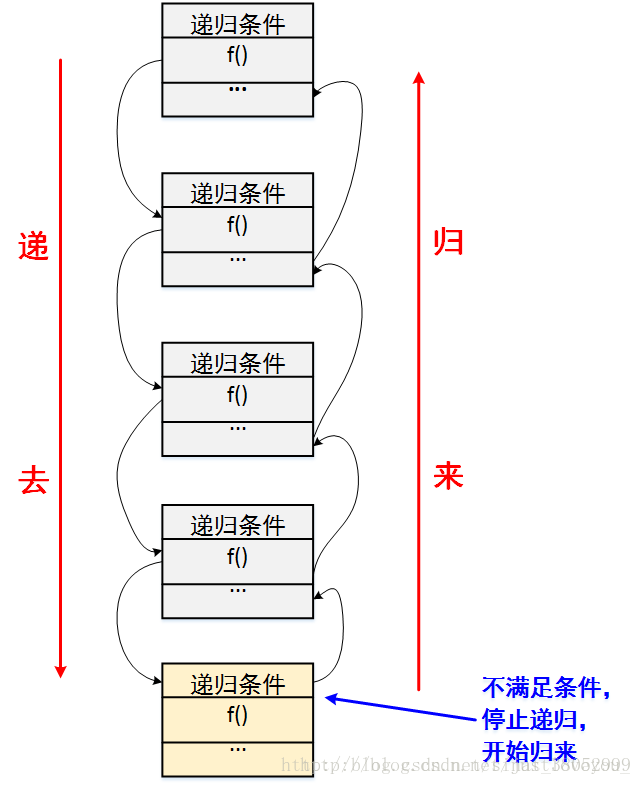
程序调用自身的编程技巧称为递归（ recursion），它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解。一般来说，递归需要有边界条件、递归前进段和递归返回段。当边界条件不满足时，递归前进；当边界条件满足时，递归返回。

递归常见形式：

指数型
排列型
组合型

我们以斐波那契数列为例：
1 1 2 3 5 8 13 21 … 即从第三项开始，每一项的值为前两项的和，那么如果我们写成函数的形式的话就是f(n)=f(n-1)+f(n-2),下面我们用代码实现求斐波那契数列第n项的数值

#include<iostream>
using namespace std;int fib(int n){if(n==1 || n==2) return 1;//边界条件return fib(n-1)+fib(n-2);
}int main()
{int n;cin>>n;cout<<fib(n);return 0;
}

每个递归过程都对应一棵递归搜索树

搜索树的每一个枝可以理解为进行了一次递归操作，对于每一层的枝数如果随着问题规模的增长而增长的话可以使用循环结构，如果枝数不随着问题规模的增长而增长的话可以使用顺序递归结构

下面我们通过图示的方式来理解上述过程，我们假设求第五个数及n=5

因为c++代码是一行一行从上向下执行的，当n=5时进入fib(5),此时n!=1 && n!=2,所以继续向下执行,执行到return fib(n-1)+fib(n-2) ,那么就是执行return fib(4)+fib(3);假设是按照从左到右的顺序执行（即先计算fib(4),再计算fib(3)）在这里插入图片描述因为我们要计算fib(4)(规模变小了),此时又进入了fib函数,此时n!=1 && n!=2,所以继续向下执行,执行到return fib(n-1)+fib(n-2) ,那么就是执行return fib(3)+fib(2);
按照约定我们要计算fib(3),此时又进入了fib函数,此时n!=1 && n!=2,所以继续向下执行,执行到return fib(n-1)+fib(n-2) ,那么就是执行return fib(2)+fib(1);
在这里插入图片描述
按照约定我们要计算fib(2),此时又进入了fib函数,此时n=2,满足递归结束条件，返回1，此时计算fib(3)时的 return fib(2)+fib(1)这个式子的fib(2)已经返回结果1，下面继续执行fib(1)，此时又进入了fib函数,此时n=1,满足递归结束条件，返回1。
在这里插入图片描述

此时fib(3) 的执行语句 return fib(2)+fib(1)这个式子已经执行完毕，return 1+1 ，即fib(3)的结果已经计算为2，将结果返回给上一层。
在这里插入图片描述
此时我们计算f(4)时的return fib(3)+fib(2)式子fib(3)已经计算完毕并将结果2返回，此时继续执行fib(2),因为n=2,满足递归结束条件，将结果1返回，此时fib(4)的return fib(3)+fib(2)已经计算完毕，return 2+1,即fib(4)计算完毕将结果返回上一层（fib的return语句中）。
在这里插入图片描述
此时我们计算f(5)时的return fib(4)+fib(3)式子fib(4)已经计算完毕并将结果3返回，此时继续执行fib(3)，按照约定我们要计算fib(3),此时又进入了fib函数,此时n!=1 && n!=2,所以继续向下执行,执行到return fib(n-1)+fib(n-2) ,那么就是执行return fib(2)+fib(1);
在这里插入图片描述
按照约定我们要计算fib(2),此时又进入了fib函数,此时n=2,满足递归结束条件，返回1，此时计算fib(3)时的 return fib(2)+fib(1)这个式子的fib(2)已经返回结果1，下面继续执行fib(1)，此时又进入了fib函数,此时n=1,满足递归结束条件，返回1。
在这里插入图片描述
此时计算fib(5)时的return fib(4)+fib(3)式子中fib(4)和fib(3)均已计算完毕，则return 3+2并将结果返回即fib(5)的值为5。

常见递归形式例题分析：

重要注意事项:
递归(dfs)算法设计最重要的就是顺序，使每种情况都不重不漏。

题目来源acwing

1. 递归实现指数型枚举

从 1∼n 这 n 个整数中随机选取任意多个，输出所有可能的选择方案。

输入格式
输入一个整数 n。

输出格式
每行输出一种方案。

同一行内的数必须升序排列，相邻两个数用恰好 1 个空格隔开。

对于没有选任何数的方案，输出空行。

本题有自定义校验器（SPJ），各行（不同方案）之间的顺序任意。

数据范围
1≤n≤15
输入样例：

输出样例：

题目分析：
任意选取多个，即等价为1-n个数，每个数有选或者不选两种情况，一共有2的n次方种情况，且每一种情况这n个数中的每一个数要么选，要么不选。我们从第一个数开始，因为所有的情况中第一个数的选择只有选和不选两种情况。
递归搜索树如下：

在这里插入图片描述

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>using namespace std;const int N = 16;int n;
int st[N];  // 状态，记录每个位置当前的状态：0表示还没考虑，1表示选它，2表示不选它void dfs(int u)
{if (u > n){for (int i = 1; i <= n; i ++ )if (st[i] == 1)printf("%d ", i);printf("\n");return;}st[u] = 2;dfs(u + 1);     // 第一个分支：不选st[u] = 0;  // 恢复现场st[u] = 1;dfs(u + 1);     // 第二个分支：选st[u] = 0;
}int main()
{cin >> n;dfs(1);return 0;
}

2. 递归实现排列型枚举

把 1∼n 这 n 个整数排成一行后随机打乱顺序，输出所有可能的次序。

输入格式
一个整数 n。

输出格式
按照从小到大的顺序输出所有方案，每行 1 个。

首先，同一行相邻两个数用一个空格隔开。

其次，对于两个不同的行，对应下标的数一一比较，字典序较小的排在前面。

数据范围
1≤n≤9
输入样例：

输出样例：

题目分析：
当要求字典序的时候，我们从小到大枚举每个数，结果就是字典序。这里我们从位置的角度来思考问题，每个位置应该放哪些数。当第一个位置放1时…,放2时…,放3时…。
递归搜索树如下：
在这里插入图片描述

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>using namespace std;const int N = 10;int n;
int state[N];   // 0 表示还没放数，1~n表示放了哪个数
bool used[N];   // true表示用过，false表示还未用过void dfs(int u)
{if (u > n)  // 边界{for (int i = 1; i <= n; i ++ ) printf("%d ", state[i]); // 打印方案puts("");return;}// 依次枚举每个分支，即当前位置可以填哪些数for (int i = 1; i <= n; i ++ )if (!used[i]){state[u] = i;used[i] = true;dfs(u + 1);// 恢复现场state[u] = 0;used[i] = false;}
}int main()
{scanf("%d", &n);dfs(1);return 0;
}

3. 递归实现组合型枚举

组合型枚举也可以考虑位置，与排列型枚举类似，但是需要一些其他的限制条件

从 1∼n 这 n 个整数中随机选出 m 个，输出所有可能的选择方案。

输入格式
两个整数 n,m ,在同一行用空格隔开。

输出格式
按照从小到大的顺序输出所有方案，每行 1 个。

首先，同一行内的数升序排列，相邻两个数用一个空格隔开。

其次，对于两个不同的行，对应下标的数一一比较，字典序较小的排在前面（例如 1 3 5 7 排在 1 3 6 8 前面）。

数据范围
n>0 ,
0≤m≤n ,
n+(n−m)≤25
输入样例：

5 3

输出样例：

题目分析：
跟排列的分析方式一样，只不过要求每一行也是字典序，这就需要额外增加限制条件。
递归搜索下如下：
在这里插入图片描述

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>using namespace std;const int N = 30;int n, m;
int way[N];void dfs(int u, int start)//u表示当前选了几个数{if (u + n - start < m) return;  // 剪枝if (u == m + 1){for (int i = 1; i <= m; i ++ ) printf("%d ", way[i]);puts("");return;}for (int i = start; i <= n; i ++ ){way[u] = i;dfs(u + 1, i + 1);way[u] = 0; // 恢复现场}
}int main()
{scanf("%d%d", &n, &m);dfs(1, 1);return 0;
}

全排列剪枝

#include<iostream>
using namespace std;
const int N = 27;
int num[N];
bool judge[N];
int n,m;
void dfs(int u){if(u>m){for(int i=1;i<=m;i++){printf("%d ",num[i]);}cout<<endl;return ;}for(int i=1;i<=n;i++){if(!judge[i]){num[u]=i;if(num[u]>num[u-1])//剪枝{judge[i]=true;dfs(u+1);judge[i]=false;}}}
}
int main()
{cin>>n>>m;dfs(1);return 0;
}