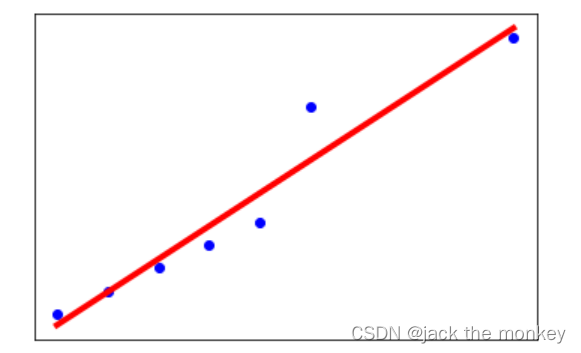
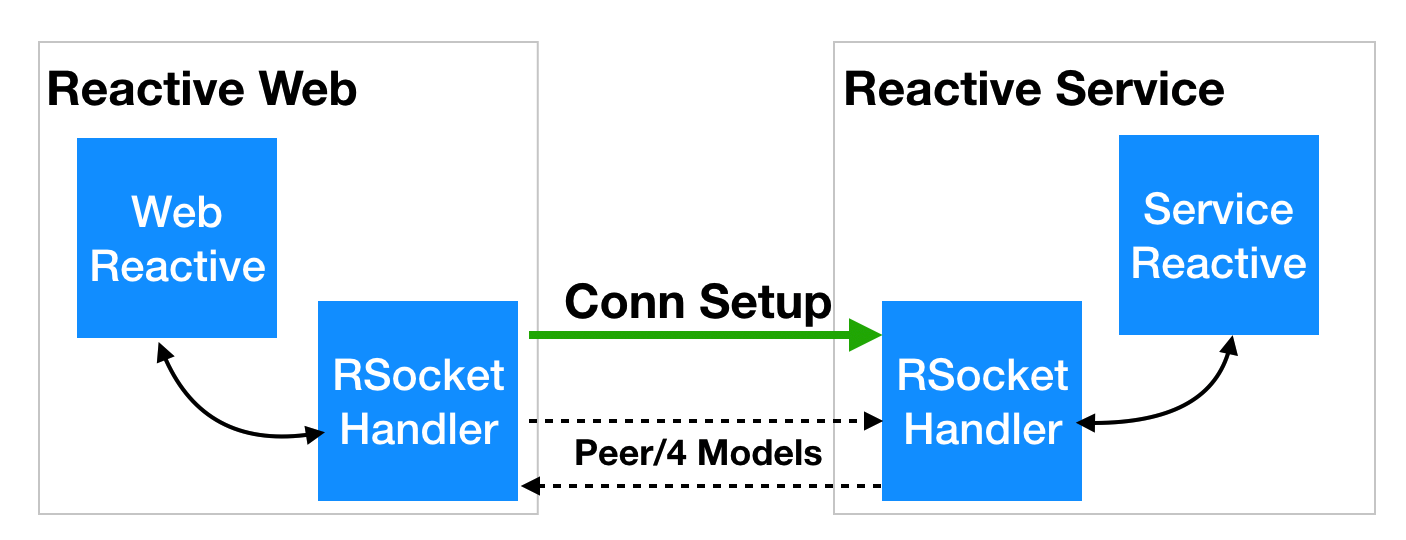
一、一元线性回归之轿车价格案例
% clear all
% clc
% x=1:10;
% y=[2650,1942,1493,1086,766,539,485,291,224,202];
% for i=1:10
% plot(x(i),y(i),'or');
% hold on
% end
% xlabel('x');
% ylabel('y');作出图像:

发现指数关系,我们另外令Z=lny
clc
clear all
x=1:10;
y=[2650,1942,1493,1086,766,539,485,291,224,202];
z=zeros(size(y));
N=length(y);
hold on
for i =1:N
z(i)=log(y(i));
plot(x(i),z(i),'ok');
end
xlabel('x');
ylabel('y');

各点基本处于一条直线附近,故可认为是z=a+bx
clear all
clc
x=1:10;
y=[2650,1942,1493,1086,766,539,485,291,224,202];
z=zeros(size(y));
N=length(y);
for i =1:N
z(i)=log(y(i));
end
[p,s]=polyfit(x,z,1)%求解参数值
输出结果:
p =
-0.2984 8.1671
s =包含以下字段的 struct:
R: [2×2 double]
df: 8
normr: 0.2316
多元线性回归:
b =
-20.5297
19.1269
8.0045
-1.5867
-0.1465
bint =-29.4308 -11.6286
10.8237 27.4301
-2.3947 18.4038
-3.4423 0.2689
-0.2873 -0.0058
r =0.0027
-0.0493
0.0429
-0.0041
0.0160
-0.0323
0.0547
-0.0306
rint =-0.0220 0.0274
-0.2312 0.1326
-0.1380 0.2238
-0.2375 0.2293
-0.0344 0.0664
-0.1565 0.0918
-0.1172 0.2266
-0.1200 0.0589
stats =0.9960 187.9515 0.0006 0.0032
别的案例:

进行多元回归的分析:
clc;clear
x1=[1.5 2.0 1.5 2.5 3.3 2.3 4.2 2.5];
x2=[5.0 2.0 4.0 2.5 3.0 3.5 2.5 3.0];
y=[96 90 95 92 95 95 94 94];
X=[ones(length(y),1),x1',x2'];
Y=y';
[b,bint,r,rint,starts]=regress(Y,X)
输出结果:
b =
83.2116
1.2985
2.3372
bint =78.8058 87.6174
0.4007 2.1962
1.4860 3.1883
r =-0.8451
-0.4829
0.4921
-0.3007
0.4920
0.6219
-0.5080
0.5308
rint =-1.4414 -0.2488
-1.5896 0.6239
-1.1901 2.1742
-2.1650 1.5637
-1.2450 2.2289
-1.1981 2.4418
-1.5594 0.5433
-1.3544 2.4159
stats =0.9089 24.9408 0.0025 0.4897
b =83.2116
1.2985
2.3372
bint =78.8058 87.6174
0.4007 2.1962
1.4860 3.1883
r =-0.8451
-0.4829
0.4921
-0.3007
0.4920
0.6219
-0.5080
0.5308
rint =-1.4414 -0.2488
-1.5896 0.6239
-1.1901 2.1742
-2.1650 1.5637
-1.2450 2.2289
-1.1981 2.4418
-1.5594 0.5433
-1.3544 2.4159
stats =0.9089 24.9408 0.0025 0.4897
得到: