🤵♂️ 个人主页:@艾派森的个人主页
✍🏻作者简介:Python学习者
🐋 希望大家多多支持,我们一起进步!😄
如果文章对你有帮助的话,
欢迎评论 💬点赞👍🏻 收藏 📂加关注+
目录
回归分析概述
线性回归
曲线估计
二元logistic回归分析
多元logistic回归分析
回归分析概述

相关分析与回归分析
- 相关分析只表明变量间相关关系的性质和程度,回归分析是要确定变量间相关的具体数学形式
- 回归分析是一种预测性的建模技术,它研究的是因变量(目标)和自变量之间的关系
回归分析的一般步骤
- 1 确定回归分析中的解释变量和被解释变量
- 2 确定回归模型
- 3 建立回归方程
- 4 对回归方程进行各种检验
- 5 利用回归方程进行预测
线性回归
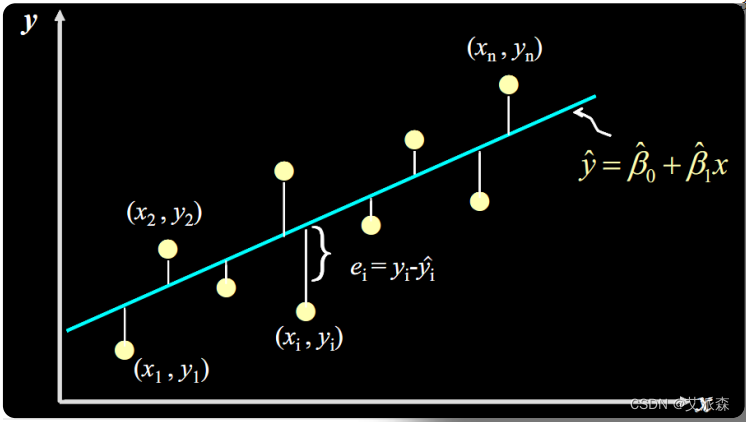
线性回归介绍
线性回归(linear regression)是分析变量间数量依存关系的统计分析方法。如果某一个变量随着另一个变量的变化而变化,并且它们的变化关系呈直线趋势,就可以用直线回归方程来定量地描述它们之间的数量依存关系,这就是线性回归分析。
一元线性回归的数学模型为:
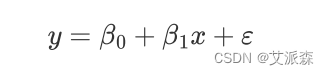
上式表明,被解释变量y的变化可由两个部分解释:
第一,由解释变量x的变化引起的y的线性变化部分,即y=β0+β1x;
第二,由其他随机因素引起的y的变化部分,即ε。
【案例】:碘含量与患病率的分析
操作步骤:
①导入数据
②【分析】-->【回归】-->【线性】
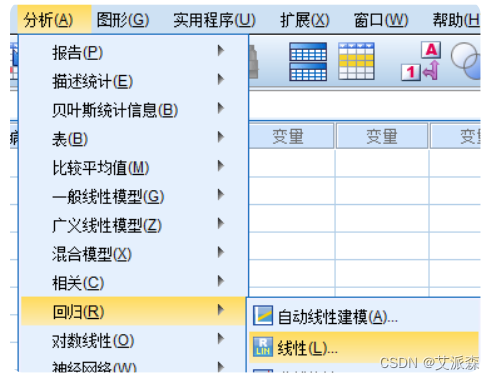
③选择自变量和应变量,点击统计
④ 勾选如下图选项,点击继续,点击图
⑤ 勾选直方图和概率图
⑥选项按钮中直接使用默认参数即可。
⑦点击“确定”按钮,查看统计结果:
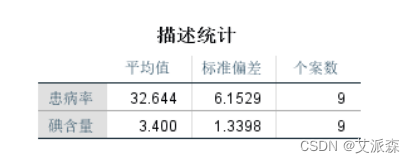
从描述统计中可以看到患病率和碘含量的平均值、标准偏差和个案数。
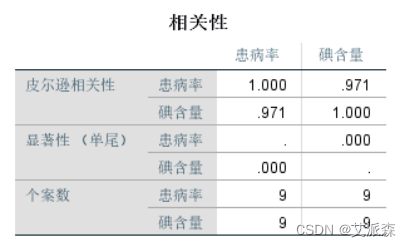
从相关性中可以看到,患病率和碘含量相关系数0.971,显著性为0。说明碘含量和患病率显著相关。

由表可见,只有一个自变量,变量选择的方法为强行输入法,也就是将所有的自变量都放入模型中。
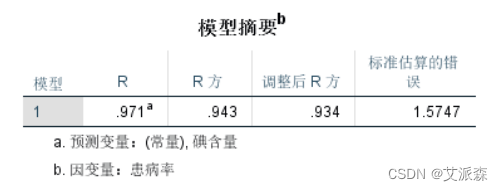
上表可看到,是对回归方程拟合情况的描述,可知相关系数的取值(R),相关系数的平方即决定系数,决定系数值为0.943, 初步判断模型拟合效果良好。
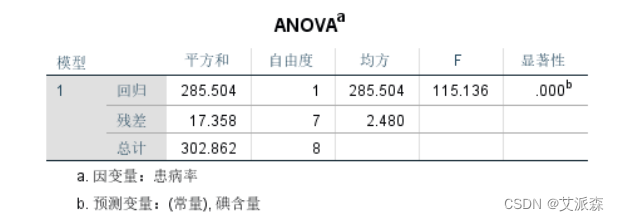
对回归方程的显著性检验,一元线性回归方程的显著性检验 的原假设H0是β1=0,即回归系数与零无显著性差异。F=115.136,P=0.000,概率P值小于α,应该拒绝原假设,认为 回归系数与零存在显著差异,被解释变量(患病率)与解释变量(碘含量)的线性关系显著,可以用线性模型描述和反映它们之间的关系。
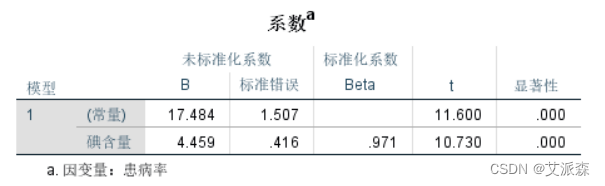
在一元线性回归分析中,回归方程的显著性检验和回归系数的显著性检验的作用是相同的,同时,回归方程的显著性检验中的F统计量等于回归系数的显著性检验中的t统计量的平方,即F=t2。
上面已经得出回归公式,接下来我们需要检验数据是否可以做回归分析,它对数据的要求是苛刻的,有必要就残差进行分析,下面是残差的正态性图形结果。
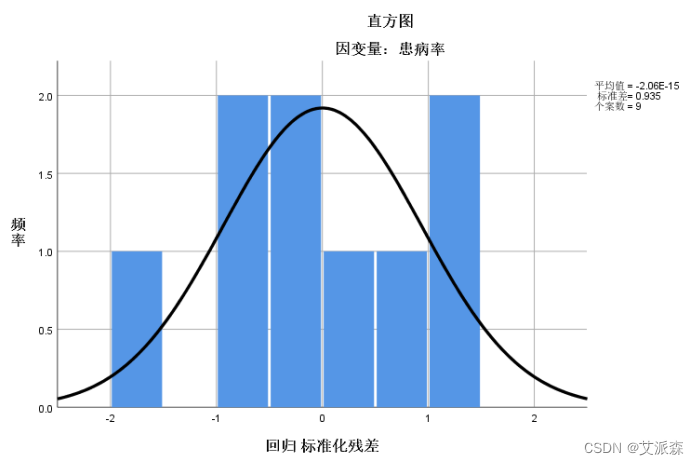

从标准化残差直方图来看,左右两侧不完全对称;从标准化残差的P-P图来看,散点并没有全部靠近斜线,并不完美。 综合而言,残差正态性结果不是最好的,当然在现实分析当中, 理想状态的正态并不多见,接近或近似即可考虑接受。
曲线估计

曲线估计介绍
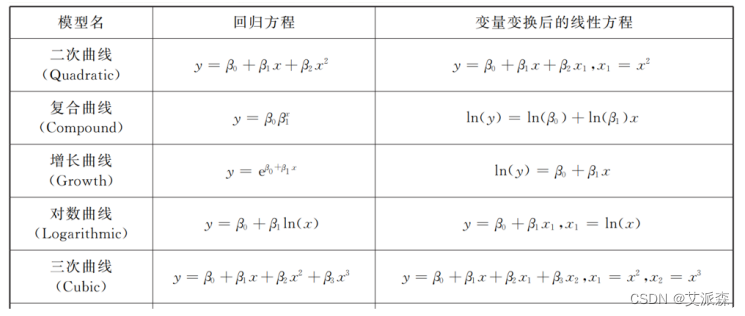
变量间相关关系的分析中,变量之间的关系并不总表现为线性关系,非线性关系也是极为常见的,可通过绘制散点图的方式粗略考察这种非线性关系。
变量之间的非线性关系可以划分为本质线性关系和本质非线性关系。
- 本质线性关系:变量关系形式上虽然呈非线性关系(如二次曲线),但可通过变量变换转化为线性关系,最终可进行线性回归分析,建立线性模型
- 本质非线性关系:变量关系不仅形式上呈非线性关系,而且无法通过变量变换转化为线性关系,最终无法进行线性回归分析和建立线性模型
注意: 曲线估计是解决本质线性关系问题的!
【案例】——年人均可支配收入与教育支出的关系分析
操作步骤:
①导入数据
②【分析】-->【回归】-->【曲线估计】
③选择因变量、个案标签等
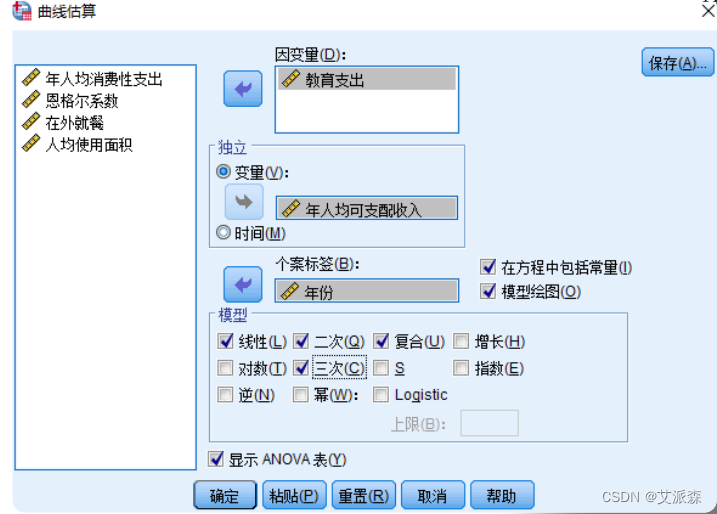
④点击“确定”按钮,结果如下:
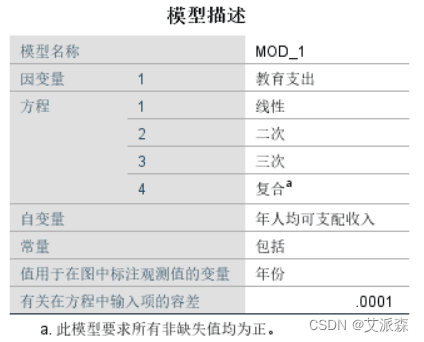
在模型描述中可以看到,因变量:教育支出,自变量为:年人均可支配收入。方程有4个,一个线性方程,一个二次方程,一个 三次方程,一个复合方程。包括常量。

从“个案处理摘要”可以看出,排除的个案为12,说明变量中所有 的个案带有“缺失值”,个案总数为28个。
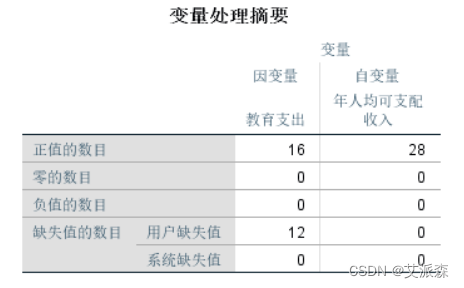
从变量处理摘要中可以看到,教育支出16个,有12个缺失值。 年人均可支配收入28个,没有缺失值。
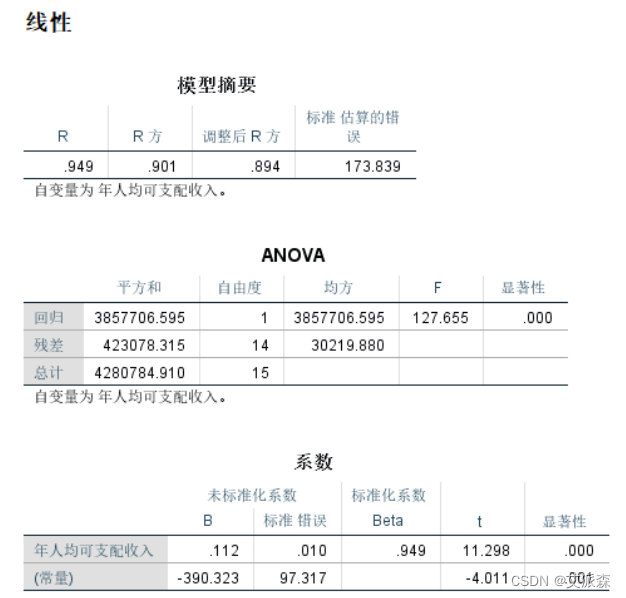
一元线性回归方程,拟合优度判定系数为0.901,显著性小于0.05。
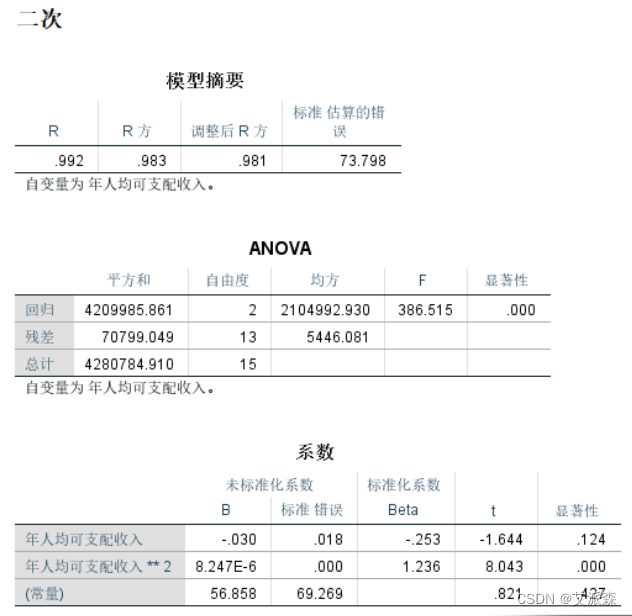
二次曲线回归方程,拟合优度判定系数为0.983。回归方程和各回归系数显著性大于0.05,表明模型不显著,二次曲线模型不合理。

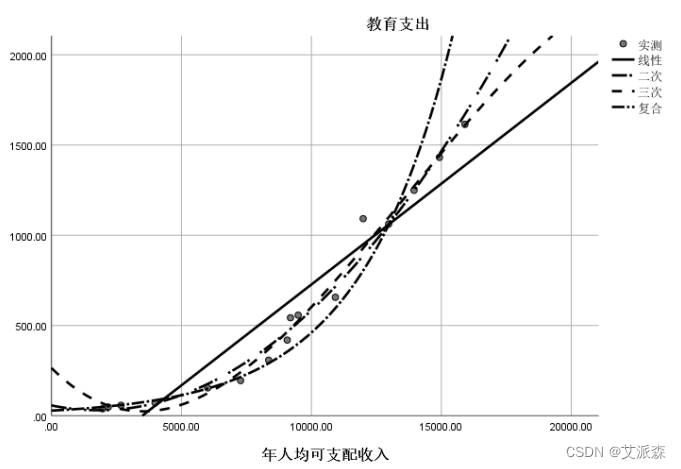
三次曲线回归方程,拟合优度判定系数为0.987(高于一元线性回归方程拟合度)。回归方程和各回归系数显著性小于0.05,表明三次曲线模型更为合理。

复合回归方程,拟合优度决定系数0.971(小于三次曲线回归方 程),各回归系数显著性小于0.05,表明模型显著。但拟合优度小于三次曲线回归方程。因此三次曲线更好反映随年人均可支配 收入增加,教育支出的变量情况。
二元logistic回归分析

在实际资料分析中,有一些因变量是分类变量,那么这样的资料就不能使用前面介绍的线性回归模型进行分析。遇到这种情况,我 们一般采取logistic回归模型对数据进行分析。
二元logistic回归是指因变量为二分类变量时的回归分析。如在采用了某种治疗方案后,病人的治疗结局是有效或无效、生存或死亡;人们对自己的生存质量是否满意;想探讨胃癌发生的危险因素,可以选择两组人群,一组是胃癌组,一组是非胃癌组,两组人群肯定有不同的体征和生活方式等。这里的因变量就是是否胃癌, 即“是”或“否”,为两分类变量。
【案例】: 为了评价某新疗法的疗效,某研究者随机抽查了40名某病患 者,治疗后一定时间内观察其康复状况。其中变量Y为康复状况 (Y=0表示未康复,Y=1表示康复),X1表示病情严重程度(1表示 严重,0表示不严重),X2表示疗法(0表示新疗法,1表示传统疗 法)。目的研究评价不同疗法对康复状况的作用有无差别?
操作步骤:
①导入数据
②【分析】-->【回归】-->【二元Logistic】
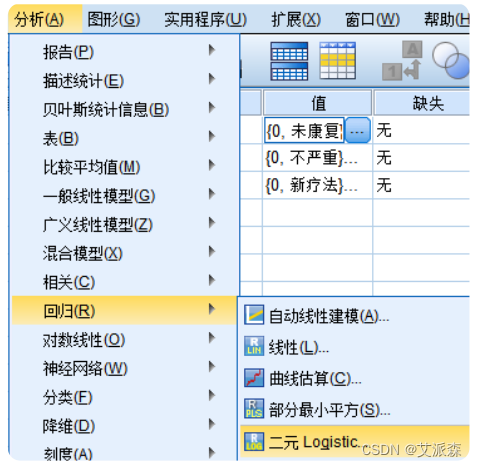
③选择因变量和协变量
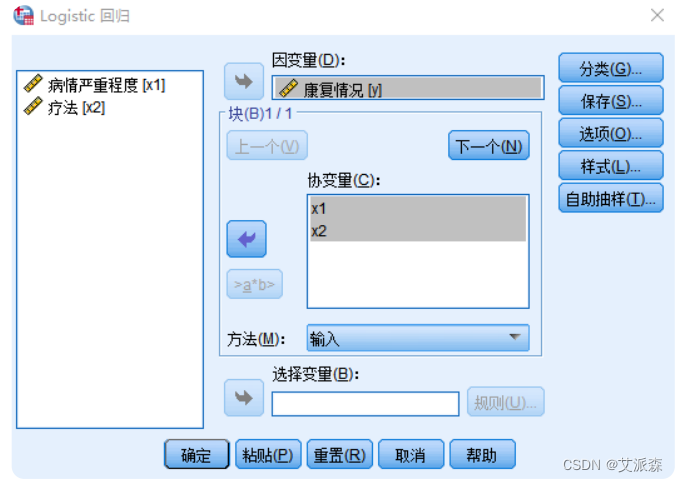
④点击“分类”按钮

当选择了分类协变量后,就可以选择参考类别,以及对比方式。
⑤点击“保存”按钮

如果勾选了“概率”和“组成员”后就会将这两个值保存到原始数据中。
⑥点击“选项”按钮
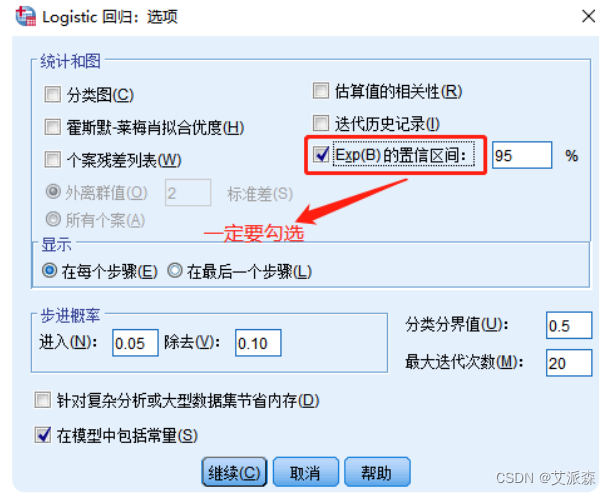
⑦点击“确定”,查看输出结果
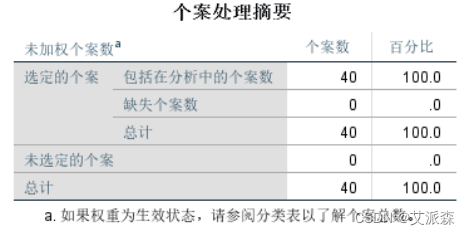
从个案处理摘要中可以看到,个案数选定40,总计也是40,未选定个案数0。

从因变量编码中可以看到,0表示未康复,1表示康复。
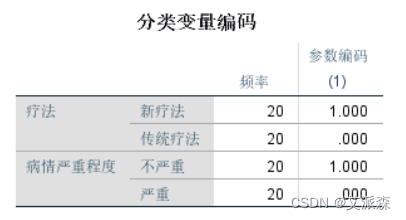
从分类变量编码中可以看到疗法有两类,新疗法和传统疗法。病情严重程度也是两类不严重和严重。
查看最终迭代分析结果:
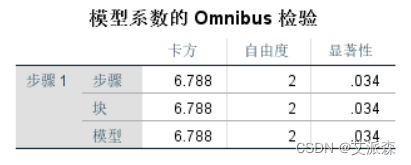
从模型系数检验中可以看到,显著性都小于0.05,表示模型总体有意义。

在模型系数检验中得到模型是有意义的,接下来看模型摘要,有两种R方决定因数,分别是0.156和0.210,R方值比较小,总体来说模型拟合优度比较小。
最终预测结果:
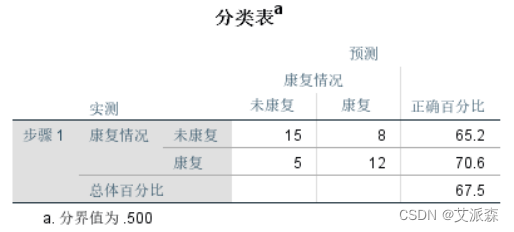
对未康复预测正确率达到65.2%,康复预测正确率达到70.6%。 总体预测正确率67.5%。

从最终模型中的变量可以看到:从常量显著性0.021小于0.05说 明常量对模型是有意义的,从病情严重程度显著性0.209大于 0.05。说明病情严重程度对模型是没有意义的,即病情严重程度 对康复和未康复没有影响。
治疗方法显著性0.022小于0.05,说明治疗方法对模型是有意义的。而且是和治疗方法值为1进行比较。治疗方法值为1表示传统疗法。得出结论,相对于传统疗法,新疗法更有易于病人康复, 换句话说,就是新疗法比传统疗法的疗效更好。
多元logistic回归分析

前面讲解的二元logistic回归分析仅适合因变量Y只有两种取值(二元logistic)的情况,如:有或无,是或否的情况。 当因变量Y具有两种以上的取值时,就要用多元logistic回归分析。
【案例】关于早餐喜好的民意调查,该调查记录了参与者的年龄、性别、婚姻状况以及生活方式是否积极,每个个案代表一个单独的响应者。调查机构想搞清楚是什么影响着受访人每天吃什么早餐。因变量“早餐选择”包括(1=早餐吧、2=燕麦类、3=谷物类),自变量暂定年龄、婚姻状况以及生活方式。
操作步骤:
①导入数据
②【分析】-->【回归】-->【多元Logistic】
③在打开的多元Logistic回归窗口,选择首选的早餐到“因变量” 中。点击“参考类别”,默认勾选的是最后一个类别,指以最后一 个类别为参照类别,用其他分类依次与之对比,考察不同水平间 的倾向。
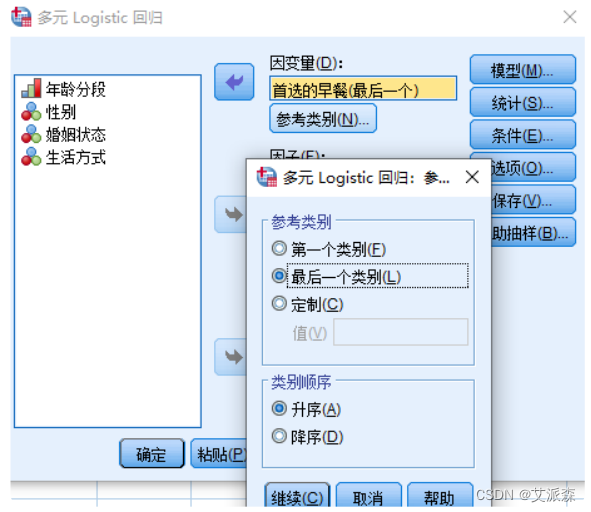
④选择年龄、婚姻状况以及生活方式选入“因子”
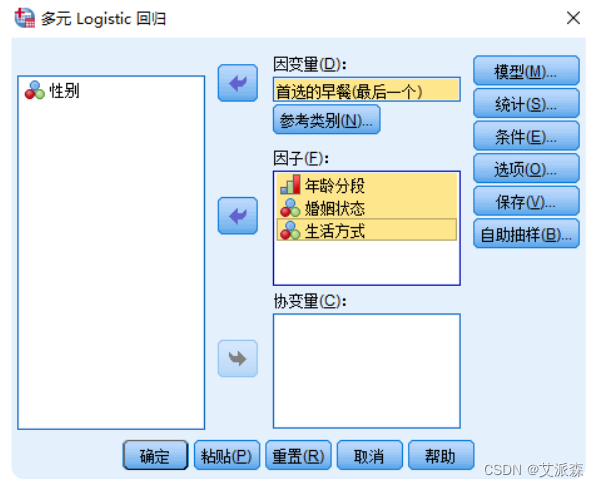
⑤主面板中,点击【模型】按钮,打开【多元logistic回归:模 型】对话框,勾选【主效应】,本例主要考察自变量年龄、生活方式、婚姻状况的主效应,暂不考察它们之间的交互作用,然后点击【继续】。
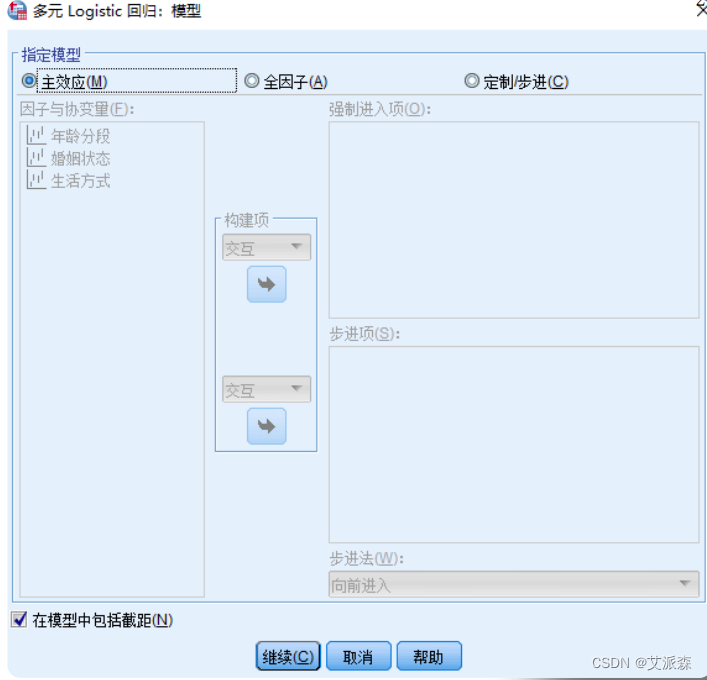
⑥ 主面板中,点击【统计】按钮,设置模型的统计量。主要【伪R方】【模型拟合信息】【分类表】【拟合优度】这几项必选,其他可以默认不勾选。这些参数主要用于说明建模的质量。
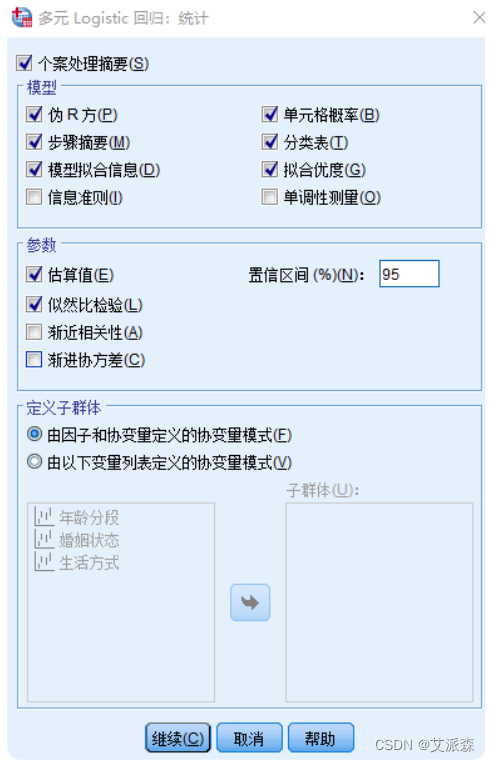
⑦主面板中,点击【统计】按钮
⑧ 点击“确定”查看输出结果:
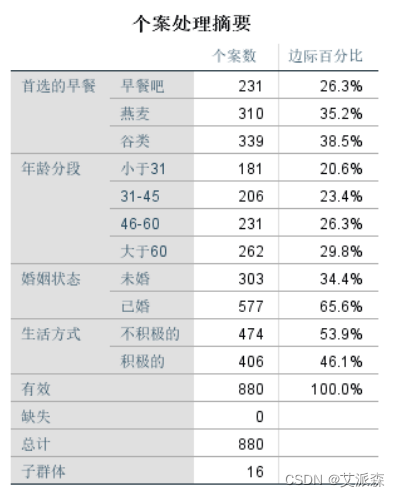
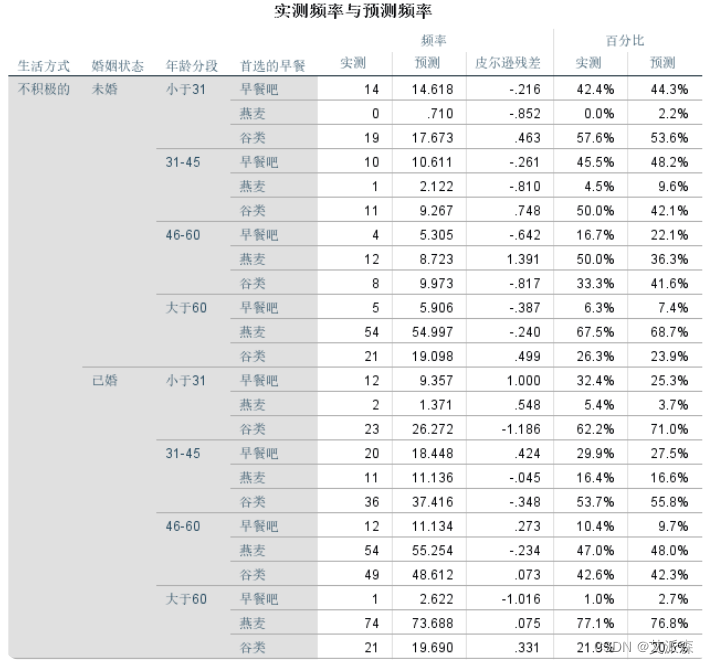
个案处理摘要表,列出因变量和自变量的分类水平及对应的个案百分比。建议在此表主要读取变量分类水平的顺序,比如自变量“年龄段”,第一个分类是“低于31岁”,第二个分类是“31- 45”,第三个分类是“45-60”,第四个分类是“60岁以上”,尤其是看清楚最后一个分类,因为我们前面参数设置时要求是以最后一 个分类为对比参照组的。

模型拟合信息表,读取最后一列,显著性值小于0.05,说明模型有统计意义,模型通过检验。
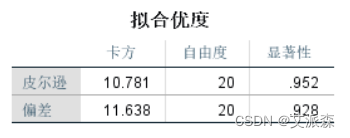
拟合优度表,原假设模型能很好地拟合原始数据,最后一列皮尔逊卡方显著性值0.952,概率较大,原假设成立,说明模型对原始数据的拟合通过检验。
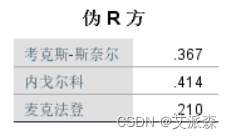
伪R方表,依次列出的3个伪R方值(类似于决定系数)均偏低, 最高0.4,说明模型对原始变量变异的解释程度一般,还有一部分信息无法解释,拟合程度并不是很优秀。
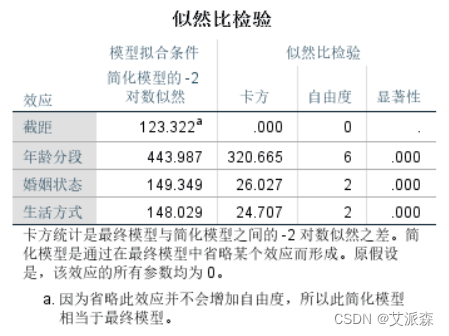
模型似然比检验表,我们能看到最终进入模型的效应包括截距、 年龄、婚姻状况、生活方式,而且最后一列显著性值表明,三个自变量(影响因素)对模型构成均有显著贡献,研究它们是有意 义的。
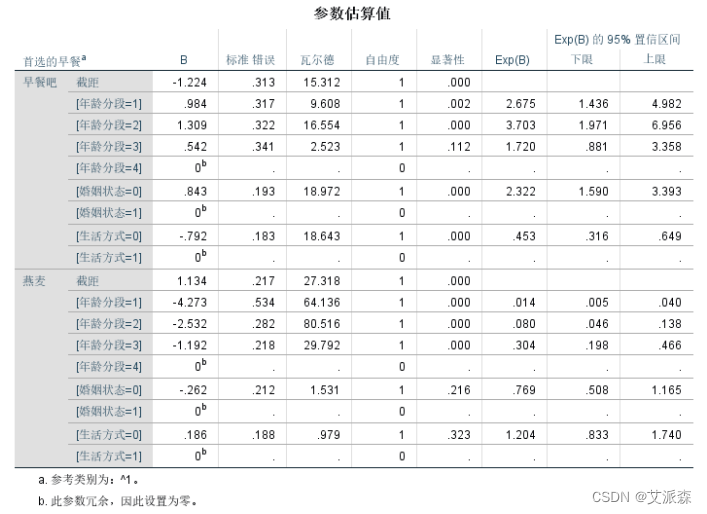
参数估计表,列出自变量不同分类水平对早餐选择的影响检验, 是多元logistic回归非常重要的结果。 第二列B值,即各自变量不同分类水平在模型中的系数,正负符号表明它们与早餐选择是正比还是反比关系。第六列是检验显著性值,此值小于0.05说明对应自变量的系数具有统计意义,对因 变量不同分类水平的变化有显著影响。

模型在预测燕麦类早餐选择倾向上准确率最高,达到77.1%,其他两个早餐选择的预测略低,模型总体预测准确率为57.4%,表现一般。前面伪R方数据显示,模型对总体变异的解释能力不足,这和总体预测准确率结论也一致。