线性回归案例分析

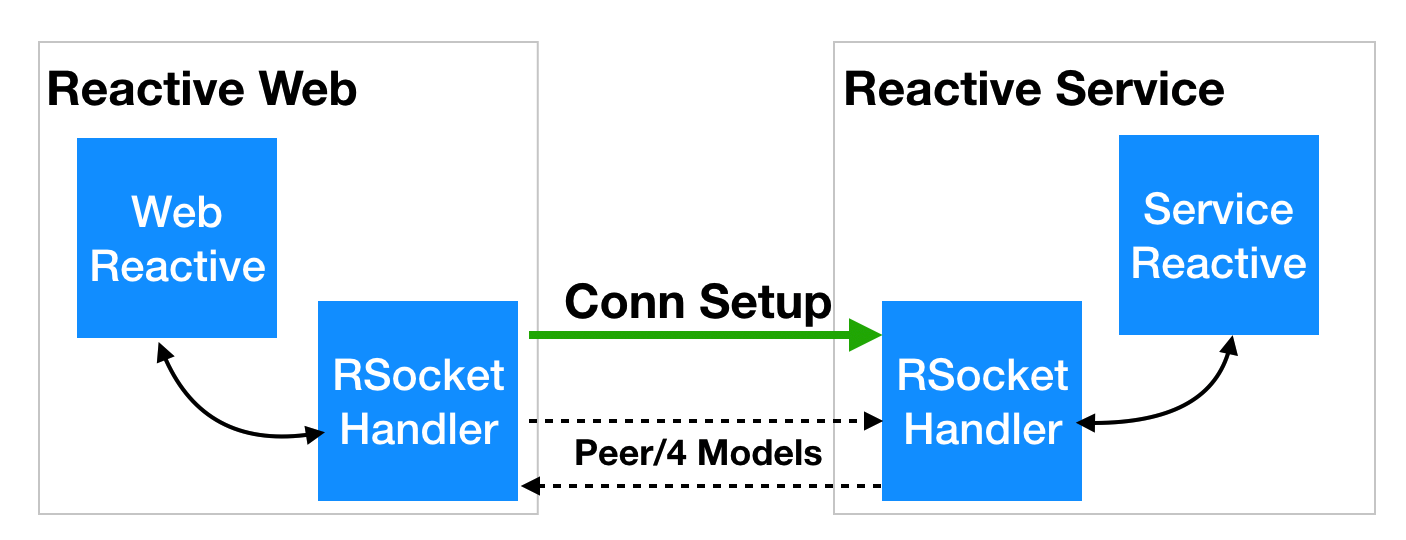
本案例是kaggle共享单车的比赛案例，先对数据集介绍

Instant 记录号

Dteday：日期

Season：季节 1=春天 2=夏天 3=秋天 4=冬天

yr：年份，(0: 2011, 1:2012)

mnth：月份( 1 to 12)

hr：小时 (0 to 23)

holiday：是否是节假日

weekday：星期中的哪天，取值为 0～6

workingday：是否工作日 1=工作日（非周末和节假日）0=周末

weathersit：天气 1：晴天，多云 2：雾天，阴天 3：小雪，小雨 4：大雨，大雪，大雾

temp：气温摄氏度

atemp：体感温度

hum：湿度

windspeed：风速

casual：非注册用户个数(非会员)

registered：注册用户个数(会员)

cnt：给定日期（天）时间（每小时）总租车人数，响应变量 y

关于线性回归知识请回顾往期两篇文章：

线性回归之原理介绍

线性回归建模思路与模型诊断(附代码)

下面直接上代码操作。

1.导入相关模块

import pandas as pd
import numpy as np
import seaborn as sns
from scipy import stats
import matplotlib.pyplot as pltfrom jupyterthemes import jtplot
jtplot.style(theme='onedork') #选择一个绘图主题
jtplot.style(ticks=True, grid=False, figsize=(6,4))plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False

2.加载数据并作描述性统计分析

data = pd.read_excel(r'D:\MLearn\共享单车\共享单车.xlsx')for i in ['season','yr','mnth','holiday','weekday','workingday','weathersit']:data[i] = data[i].astype(object) #声明离散型变量data.drop(['instant','dteday','casual','registered'],axis=1).describe(include='object')des = data.drop(['instant','casual','cnt','registered'],axis=1).describe().T
des['极差'] = des['max'] - des['min']
des['离散系数'] = des['std']/des['mean']
des.T.round(decimals=3)

观察结果：

离散型变量一共7个：季节、年份、月份、是否节假日、是否周末、是否工作日和天气

数据无缺失，都是731条数据记录。

连续型变量有4个，气温摄氏度（temp），体感温度（atemp），湿度（hum）和风速（windspeed）

从数据集中趋势看，中位数与均值基本持平，说明数据分布比较集中，

从数据离散程度看，湿度的变异程度最大，但离散系数最低，波动幅度最低；而风速的变异程度低，但波动幅度大。

3.对目标变量进行正态性检验

from scipy.stats import norm, skewa = data['cnt']sns.distplot(a, fit=norm)
(mu, sigma) = norm.fit(a)
print(mu, sigma)
print('Kurtosis: %f' % a.kurt())
print('Skewness: %f' % a.skew())fig = plt.figure()
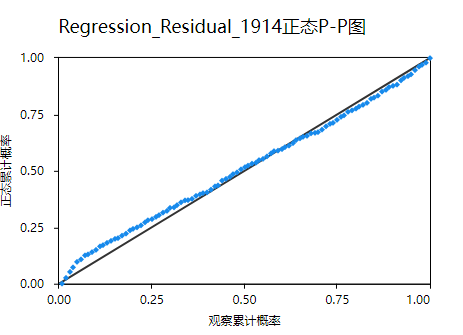
res = stats.probplot(a, plot=plt)
plt.show()

结果如下：

拟合的均值为4500，方差1935。蓝色线不完全分布在红色上，峰度值为-0.8，偏度-0.04，表明数据呈现轻微低峰态的左偏分布。

再研究一下目标变量：看看时间跟租赁量的走势图：

data['year_month'] = data.dteday.dt.strftime('%Y-%m') #年月日转换为年月# 做每天租赁散点图和每月均值
group_month = data.groupby('year_month')['cnt'].mean()
group_month.index = pd.to_datetime(group_month.index)
plt.figure(figsize=(16,5))
plt.plot(data.dteday, data.cnt, '-', color = 'b', label = '每天租赁数量', alpha=0.5)
plt.plot(group_month.index, group_month.values, '-o', color='orange', label = '每月租赁数量均值')
plt.legend()
plt.show()

1.共享单车的租赁情况2012年整体比2011年有所增长；

2.租赁数量随月份波动且每年波动幅度相似；

3.有很多局部波峰波谷值且2012年波动情况比2011年大

4.对影响租赁量因素做整体探索

sns.pairplot(data ,x_vars=['holiday','workingday','weathersit','season','weekday', 'temp','atemp','hum','windspeed'] ,y_vars=['casual','registered','cnt'] , plot_kws={'alpha': 0.5})plt.show()

结果如下，就是变量与目标的散点图分布：

1.会员在工作日出行量多，非工作日少，非会员则相反；

2.无论是会员还是非会员，节假日出行量多于非节假日；

3.租赁数量随天气等级上升而减少；

4.一季度出行量低于其他季度出行量

5.会员在星期一~星期五的出行量多于周六、周日，而非会员相反

6.租赁数量随风速增大而减少；

7.温度、湿度对非会员影响比较大，对会员影响较小

8.总体租赁量随着温度升高而升高

5.探索特征与目标之间的关系

对于离散变量，列举季节、月份对目标的影响，其余变量同理操作。

sns.violinplot(data=data[['season','cnt']],x="season",y="cnt")
plt.show()

能看出来每个季节骑行量的分布不同 barplot利用矩阵条的高度反映数值变量的集中趋势

fig,ax = plt.subplots()
sns.barplot(data=data[['mnth', 'cnt']], x="mnth",y="cnt")
ax.set(title="Monthly distribution of counts")
plt.show()

可以看出，一年12月份，单车投放量先上升后下降，峰值出现再6~8月份

对于连续变量，由于变量不多，直接给出相关关系图查看：

corrmatt = data[['temp','atemp','hum','windspeed','cnt']].corr()
plt.subplots(figsize=(6,4))
mask = np.array(corrmatt)
mask[np.tril_indices_from(mask)] = False
heatmap = sns.heatmap(corrmatt,annot=True,mask=mask,cmap="Blues")
plt.show()

1.气温摄氏度、体感温度与骑行量的相关性大于0.5，而湿度、风速与骑行量的相关性很低

2.气温摄氏度与体感温度的相关性高达0.99

再进一步挖掘，

#按温度取租赁额平均值
data['temp_group'] = pd.cut(data['temp'], bins=[0.05*i for i in range(21)],right=False)
temp_rentals = data.groupby(['temp_group'], as_index=True).agg({'casual':'mean', 'registered':'mean','cnt':'mean'})
temp_rentals .plot(title = 'The average number of rentals initiated per hour changes with the temperature')
# plt.xticks(rotation=45)
plt.show()

随着温度的上升，租赁量也增加，在0.7附近达到最高峰，之后随着温度升高，租赁量开始缓慢下降

6.假设检验

对于双样本，这里展示年份对目标影响的显著性检验，其余操作同理。

arg = []
li = [2011,2012]
for i in data['yr'].value_counts().index:arg.append(data[data['yr'] == i]['cnt'])sns.boxplot(data=arg,palette='deep') #箱线图,设置6种颜色；调色板
plt.show()# stats.f_oneway(*arg)
des = data['cnt'].groupby(data['yr']).describe()
des['cov'] = des['std']/des['mean']
des

箱线图如下图：

可见2011和2012骑行量均值有很大差别，下面进一步从统计学上验证该差异显著

#方差齐性检验 H0:两组数据方差相同
year2011 = data[data['yr'] == 0]['cnt']
year2012 = data[data['yr'] == 1]['cnt']
leveneTestRes = stats.levene(year2011, year2012, center='median')
print('w-value=%6.4f, p-value=%6.4f' %leveneTestRes)

检验结果：

p小于0.05，拒绝原假设，即两组数据方差不相同，有显著差异。因此不能采用t检验，要采取大样本u检验

from scipy.stats import normdes['S'] = des['std']**2  #总体方差的无偏估计,describe内置的std分母是n-1
des[['count','mean','S']]
u = (des['mean'][0]-des['mean'][1])/np.sqrt(np.sum(des['S']/des['count'])) #检验统计量
p = norm.cdf(u,0,1) #概率密度函数在 负无穷 到 u上的积分，也就是概率print('u-value=%6.4f, p-value=%6.4f' % (u,2*p)) #双侧检验，乘以2

检验结果p远小于0.05，因此可以认为均值有显著差异。

对于多样本检验，也就是要进行方差分析，这里以季节为例：

arg = []
li = []
for i in data['season'].value_counts().index:li.append(i)arg.append(data[data['season'] == i]['cnt'])sns.set_style('whitegrid') #箱线图，观察异常值
jtplot.style(theme='onedork') #选择一个绘图主题
jtplot.style(ticks=True, grid=False, figsize=(10, 8))
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=Falsesns.boxplot(data=arg,palette='deep') #箱线图,设置6种颜色；调色板
# plt.xticks(range(16),li,rotation=90)
plt.show()print('单因素方差分析：',stats.f_oneway(*arg))

箱线图与检验结果如下：

p值远小于0.05，因此，季节对均值有显著影响。

注：除了单因素方差分析，我们还有多因素方差分析，就是考虑两个变量交互作用的影响，以下代码实现了这个过程（本节的建模不考虑这种影响）

import statsmodels.formula.api as smf
import statsmodels.api as smli = ['season','mnth','weathersit']for n,i in enumerate(li):for j in li[n+1:]:# smf:最小二乘法,构建线性回归模型anal = smf.ols('cnt ~ C({}) + C({}) + C({})*C({})'.format(i,j,i,j), data=data).fit()# anova_lm:多因素方差分析re = sm.stats.anova_lm(anal)re = pd.DataFrame(re)if list(re['PR(>F)'])[2] > 0.01:print('{}和{}交互作用对单车投放量影响无显著差别，考虑无交互作用的情况'.format(i,j))#考虑无交互作用的方差分析anal = smf.ols('cnt ~ C({}) + C({})'.format(i,j), data=data).fit()# anova_lm:多因素方差分析re = sm.stats.anova_lm(anal)else:print('{}和{}交互作用对单车投放量影响有差别'.format(i,j))print(re)print('********************************************************')

7.特征工程

基于前面步骤的分析，我们可以筛选、构造一些特征。然后做一定的特征工程处理，离散变量需要连续化，一般采用one-hot编码（独热编码）

feature_col = ['season','mnth','weathersit','yr']
for feature in feature_col:data[feature] = data[feature].astype('object')season_di = {1:'spring',2:'summer',3:'autumn',4:'winter'}
month_di = {1:'Jan',2:'Feb',3:'Mar',4:'Apr',5:'May',6:'Jun',7:'Jul',8:'Aug',9:'Sep',10:'Oct',11:'Nov',12:'Dec'}
weather_di = {1:'sunny',2:'fog',3:'rain',4:'snow'}
year_di = {0:2011,1:2012}data_cat = data[feature_col]
data_cat['season'] = data_cat['season'].replace(season_di)
data_cat['mnth'] = data_cat['mnth'].replace(month_di)
data_cat['weathersit'] = data_cat['weathersit'].replace(weather_di)
data_cat['yr'] = data_cat['yr'].replace(year_di).astype(object)data_cat = pd.get_dummies(data_cat) #独热编码

如有需要，还要进行归一化处理，以后会专门出一起关于归一化的问题，利用下面代码可以进行归一化处理。本次建模做了均值标准差归一化处理。

from sklearn.preprocessing import MinMaxScaler #线性函数归一化
from sklearn.preprocessing import StandardScaler #均值与标准差归一化

8.模型建立与调参

采用L2正则进行建模，利用网格搜索寻找最优超参数，本次建模采取r2评价指标（也就是可决系数）

from sklearn.linear_model import RidgeCV
from sklearn.linear_model import LassoCV
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import train_test_split
from sklearn.metrics import make_scorer,log_loss,r2_score,mean_squared_error #评价指标，损失函数

切分训练测试集，这里二八分：

X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2,random_state=0)

首先，随机挑选几个超参数：

alphas= [0.1,1,5,10]model = RidgeCV(alphas=alphas,fit_intercept=True,scoring=None, cv=5)model.fit(X_train,y_train)y_pred = model.predict(X_test)
# print('train of mean_squared_error is:',mean_squared_error(y_train,model.predict(X_train)))
# print('test of mean_squared_error is:',mean_squared_error(y_test,y_pred))
print(model.alpha_)
print('train of R2 is:',r2_score(y_train,model.predict(X_train)))
print('test of R2 is:',r2_score(y_test,y_pred))

结果如下：

然后从1~10之间利用网格搜索逐步寻找最佳的超参数，笔者一共迭代了4次，最终找到了合适的超参数C=4.213

第一轮迭代：

alphas= np.linspace(1,10,21)
model = RidgeCV(alphas=alphas,fit_intercept=False,scoring=None, cv=5)
model.fit(X_train,y_train)
y_pred = model.predict(X_test)
print(model.alpha_)
print('train of R2 is:',r2_score(y_train,model.predict(X_train)))
print('test of R2 is:',r2_score(y_test,y_pred))

第二轮迭代：

alphas= np.linspace(3.7 ,4.6,21)
model = RidgeCV(alphas=alphas,fit_intercept=False,scoring=None, cv=5)
model.fit(X_train,y_train)
y_pred = model.predict(X_test)
print(model.alpha_)
print('train of R2 is:',r2_score(y_train,model.predict(X_train)))
print('test of R2 is:',r2_score(y_test,y_pred))

第三轮迭代：

alphas= np.linspace(4.15 ,4.24,21)
model = RidgeCV(alphas=alphas,fit_intercept=False,scoring=None, cv=5)
model.fit(X_train,y_train)
y_pred = model.predict(X_test)
print(model.alpha_)
print('train of R2 is:',r2_score(y_train,model.predict(X_train)))
print('test of R2 is:',r2_score(y_test,y_pred))

第四轮迭代：

alphas= np.linspace(4.2085 ,4.2175,21)
model = RidgeCV(alphas=alphas,fit_intercept=False,scoring=None, cv=5)
model.fit(X_train,y_train)
y_pred = model.predict(X_test)
print(model.alpha_)
print('train of R2 is:',r2_score(y_train,model.predict(X_train)))
print('test of R2 is:',r2_score(y_test,y_pred))

可见，第四轮后，训练集和测试集的R2没有变化了，且两者都是0.8369.说明超参数已经最优了。

9.诊断方差与偏差

绘制学习曲线和验证曲线去观察偏差与方差，先来看学习曲线：

from sklearn.linear_model import Ridge
from sklearn.model_selection import learning_curve #学习曲线,方差与偏高的诊断
from sklearn.model_selection import ShuffleSplitcv = ShuffleSplit(n_splits=10, test_size=0.3, random_state=0)li = np.linspace(0.1,1,10)
train_sizes, train_loss, test_loss = learning_curve(Ridge(alpha=4.213,fit_intercept=False,random_state=0),X, y, cv=cv, scoring ='r2',train_sizes=li)train_score = np.mean(train_loss,axis=1)
test_score = np.mean(test_loss,axis=1)
plt.figure()
plt.plot(li,train_score,'o-',color = 'b',label = 'Training')
plt.plot(li,test_score,'o-',color = 'r',label = 'Testing')
# plt.plot(li,[0.115 for i in range(len(li))],'--',color = 'g',label = 'Desired')
plt.legend(loc='best')
plt.title('learning curve')
plt.xlabel('traing set size')
plt.ylabel('R2')
plt.show()

注：这里做了10折交叉验证，利用ShuffleSplit模块实现的，举一个例子解释它的工作原理

假设参数输入如下：

ShuffleSplit(n_splits=5, test_size=0.2, random_state=0)

利用20%数据集作为验证集，80%作为训练集，对同一份数据集做重复5次这样的过程。然后训练时，5次采样都建模，最后用采样的5次验证集的平均结果作为最终的输出结果。

注意，这里与我们常说的交叉验证不太一样，因为每次的验证集样本可能有重复的，而我们的交叉验证的每次的测试集都是不一样的。源码也给出了解释。

严格的交叉验证是下面这样的（估计大家这张图不陌生，利用模块kflod可以实现）

好了，回到正题，我们解读我们模型的学习曲线：

解读学习曲线：一开始，训练集样本只有10%的时候，模型严重过拟合，训练集R2表现比测试集的好了很多，随着样本增加，观察到，训练集R2指标降低，测试集上升，模型过拟合效果逐渐被改善，当用完所有样本进行训练时，二者的R2已经非常接近了，模型拟合效果良好。

再来看验证曲线的表现，

from sklearn.model_selection import validation_curvecv = ShuffleSplit(n_splits=10, test_size=0.3, random_state=0)
li = np.linspace(0.1,10,21)train_loss, test_loss = validation_curve(Ridge(fit_intercept=False,random_state=0),X, y, cv=cv,scoring ='r2',param_name='alpha',param_range=li)train_score = np.mean(train_loss,axis=1)
test_score = np.mean(test_loss,axis=1)
plt.figure()
plt.plot(li,train_score,'o-',color = 'b',label = 'Training')
plt.plot(li,test_score,'o-',color = 'r',label = 'Testing')
plt.legend(loc='best')
plt.title('validation curve')
plt.xlabel('value of C')
plt.ylabel('R2')
plt.show()

刚开始看起来，好像训练集测试集的R2相差很大，但是我们注意到纵坐标的刻度，其实误差已经在0.01范围了。解读这个验证曲线：

一开始，对超参数惩罚很低时，模型过拟合，随着惩罚的增加，训练集效果一直下降，而测试集先上升后下降，说明模型过拟合效果减轻，当达到一定程度后，继续加大惩罚，训练集和测试集效果都下降。这就说明超参数的调节对于最优模型的选择是多么的重要了。

最后我们看看拟合出来特征系数：

# Plot important coefficients
coefs = pd.Series(model.coef_, index = X_train.columns)
print("Ridge picked " + str(sum(coefs != 0)) + " features")#系数值变量排序
imp_coefs = pd.concat([coefs.sort_values()])
imp_coefs.plot(kind = "barh")
plt.title("Coefficients in the OLS Model")
plt.show()