PID控制算法公式

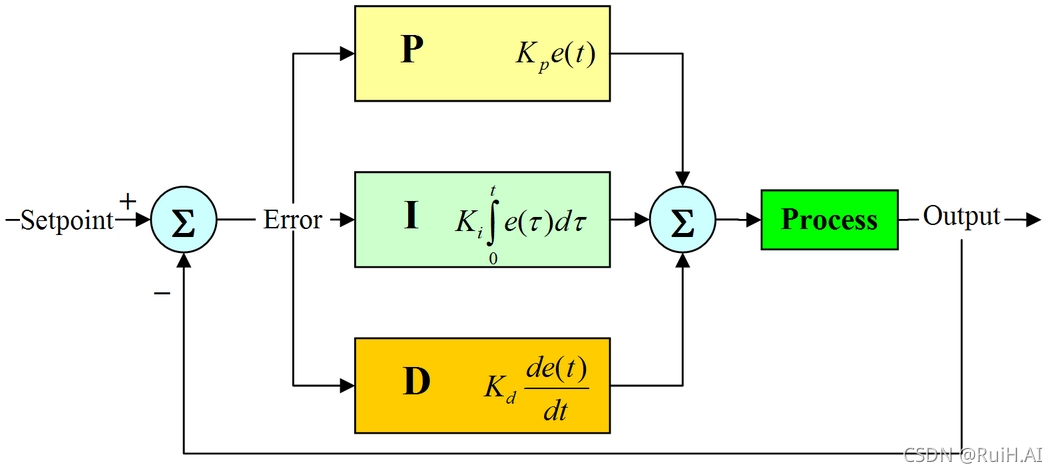
原理

PID控制是一种在工业生产中应用最广泛的控制方法，其最大优点是不需要了解被控对象精确的数学模型，只需要在线根据被控变量与给定值之间的偏差以及偏差的变化率等简单参数，通过工程方法对比例系数$K_P$，积分时间$K_I$，微分时间$K_D$三个参数进行调整，就可以得到满意的效果。

PID控制器的微分方程为：
$$u(t)=K_P[e(t)+\frac{1}{T_I}{\int }_0^{t}e(t)dt+T_D\frac{de(t)}{dt}]$$

• $e(t)$—给定值与被控变量的偏差
• $K_P$—比例系数
• $K_I$—积分时间常数
• $K_D$—微分时间常数
• $t$—从开始调节到输出当前控制量所经过的时间间隔

对上式左右两边分别进行拉氏变换，可得PID控制器的传递函数为：
$$G(s)=\frac{U(s)}{E(s)}=K_P(1+\frac{1}{T_{I}s}+T_{D}s)$$
注：此处的传递函数仅为PID控制器，是不含反馈环节的。

由于计算机只能处理数字信号，故将连续信号离散化，采样周期为T：
$$u(k)=K_P\{e(k)+\frac{T}{T_I}\sum _{i=0}^{k}e(i)+\frac{T_D}{T}[e(k)-e(k-1)]\}$$
继续化简，用$K_I$代替$\frac{K_{P}T}{T_I}$，用用$K_D$代替$\frac{K_P{T}_D}{T}$
$$⟹u(k)=K_{P}e(k)+K_I\sum _{i=0}^{k}e(i)+K_D[e(k)-e(k-1)]$$

• 比例系数$K_P$
• 积分系数$K_I$
• 微分系数$K_D$

参数作用

1. 比例系数

• 比例环节是PID控制器必不可少的环节，作用是放大误差信号，提高控制器对偏差信号的灵敏度
• 当比例系数过大时，会使系统的超调量增加，出现振荡。控制系统的灵敏性和稳定性是相互矛盾的，比例系数的选择只能在稳定性与灵敏性间折中
• 单纯的比例环节会引入稳态误差，由原理性稳态误差和结构性稳态误差构成

2. 积分系数

• 积分环节的主要作用是改善系统的稳态性能，消除系统的稳态误差
• 当积分时间常数$T_I$的减小可能导致系统超调量T增加，过小的$T_I$会造成系统的振荡甚至不稳定，因为积分环节总是滞后于偏差的变化，过强的积分作用还会造成积分饱和；$T_I$的增大可能使系统趋于稳态值的速度减慢

3. 微分系数

• 微分环节根据偏差的变化趋势输出控制量，在偏差值发生较大变化时输出校正信号
• 当微分时间常数$T_D$增大时，系统相应速度加快，调节时间减小，但过大时，会使响应过程提前制动，从而延长调节时间并出现余差

PID算法及改进

两个基本类型

位置型PID控制

位置型PID控制算法，适用于不带积分元件的执行器，比如舵机和温控系统，执行器的动作位置与其输入信号呈一一对应的关系。PID控制器根据第k次被控对象采样结果与设定值之间的偏差$e(k)$计算出第k次采样时所输出的控制量。位置型PID算法的数学表达式为(即上述推导)：
$$u(k)=K_{P}e(k)+K_I\sum _{i=0}^{k}e(i)+K_D[e(k)-e(k-1)]$$

• 之所以叫位置型PID控制，也是因为控制器的输出$u(k)$对应执行器的实际位置
• 由于误差积累项${\sum }_{i=0}^{k}e(i)$，当前的输出$u(k)$与过去所有状态有关
• 需要积分限幅和输出限幅

增量型PID控制

与位置型PID算法相对应的是增量型PID算法，增量型算法适用于自身带有积分记忆元件的执行器，比如步进电机，此类执行器的特点是：执行器的动作终点位置与之前每次输入信号的累加值有关，每次执行器输入的控制信号决定本次执行器动作终点位置相对于上一次动作终点位置的改变量。增量型PID算法的数学表达式为：
$$\Delta u(k)=u(k)-u(k-1)=K_P[e(k)-e(k-1)]+K_{I}e(k)+K_D[e(k)-2e(k-1)+e(k-2)]$$

• 增量型PID中不需要累加误差，控制量$u(k)$仅与最近3次采样值有关
• 无需积分限幅，只需输出限幅

积分环节改进的PID控制

积分分离的PID控制

积分分离的基本思想是，当被控量与预设量偏差较大时，取消积分量，以免积分量使系统稳定性降低，超调量增大；当被控值接近定值时，引入积分控制，以消除静差，算法原理如下：
计算$e(k)=R-c(k)$，设定阈值$\epsilon$，控制器输出量为
$$u(k)=K_{P}e(k)+\beta K_I\sum _{i=0}^{k}e(i)+K_D[e(k)-e(k-1)]$$
若$\left|e(k)\right|>\epsilon$，\beta = 0；若$\left|e(k)\right|\le \epsilon$，\beta = 1
注：在$\left|e(k)\right|>\epsilon$时，虽然控制器输出控制量中不含积分项，但控制器仍然将每次采样后所得的偏差值进行累加

变速积分的PID控制

变速积分的基本思想是改变积分项的累加速度，使其与偏差大小相对应，当偏差值较大时，积分速度减慢，当偏差值较小时，积分速度加快。这样就可以抑制积分环节产生超调，同时缩短调节时间，算法原理如下：
计算$e(k)=R-c(k)$，设定系数值$A$，控制器输出量为
$$u(k)=K_{P}e(k)+K_I\sum _{i=0}^k\alpha e(i)+K_D[e(k)-e(k-1)]$$
其中，$\alpha =\frac{A-|e(k)|}{A}$。为使$\alpha =\frac{A-|e(n)|}{A}\in [0,1]$区间之内，需使$A>{\left|e(k)\right|}_{max}$

抗积分饱和的PID控制

积分饱和现象：当控制系统输出的被控变量长时间未达到给定值时，这段时间内积分环节所产生的控制量将形成一个很大的积累值，PID控制器的输出控制量将由于积分环节的累加作用而不断增加。当控制量达到或超出执行机构的输入信号上下限时，此后执行器将进入饱和区，不再随着输入控制量的增加而进一步动作。当偏差值反向时，控制器的输出控制量需要很长时间才能退出饱和区，这段时间内执行器停留在极限位置而暂时失去控制。

所谓抗积分饱和法，就是在计算$u(k)$时，首先判断上一时刻的控制量$u(k-1)$是否已经超出了极限范围：若$u(k-1)>umax$，则只累加负偏差，如果$u(k-1)<umin$，则只累加正偏差。

微分环节改进的PID控制

不完全微分PID控制

不完全微分算法即在原微分环节上添加一个具有低通滤波作用的惯性环节，因此不完全微分环节的传递函数为：
$$G(S)=\frac{U_D(s)}{E(s)}=\frac{K_P{T}_{D}s}{1+T_{f}s}$$
经化简，
$$(1+T_{f}s)U_D(s)=K_P{T}_{D}sE(s)⟹U_D(s)+T_{f}s{U}_D(s)=K_P{T}_{D}sE(s)$$
经拉氏反变换，写成微分方程为
$$u_D(t)+T_f\frac{d{u}_D(t)}{dt}=K_P{T}_D\frac{de(t)}{dt}$$
取采样时间$T$，将上式离散化得
$$u_D(k)+T_f\frac{u_D(k)-u_D(k-1)}{T}=K_P{T}_D\frac{e(k)-e(k-1)}{T}$$
整理得
$$u_D(k)=\frac{T_f}{T+T_f}{u}_D(k-1)+\frac{K_P{T}_D}{T+T_f}[e(k)-e(k-1)]$$
令$\alpha =\frac{T_f}{T+T_f}$，则$1-\alpha$ = $\frac{T}{T+T_f}$，因此不完全微分算法公式为
$$u_D(k)=K_D(1-\alpha )[e(k)-e(k-1)]+\alpha u_D(k-1)$$

微分先行PID控制

微分先行算法适用于给定量频繁改变的控制系统，被控值与给定值的偏差若出现频繁的跳变，如果对偏差进行微分，会使微分结果产生剧烈的脉冲变化，不利于系统稳定，而控制系统的被控量输出一般不会产生突变，采用微分先行算法可改善系统的动态特性，有利于系统的稳定。

微分先行即将对偏差的微分改为对被控变量的微分，微分环节的输出为
$$u_D(k)=\frac{K_P{T}_D}{T}[c(k)-c(k-1)]$$