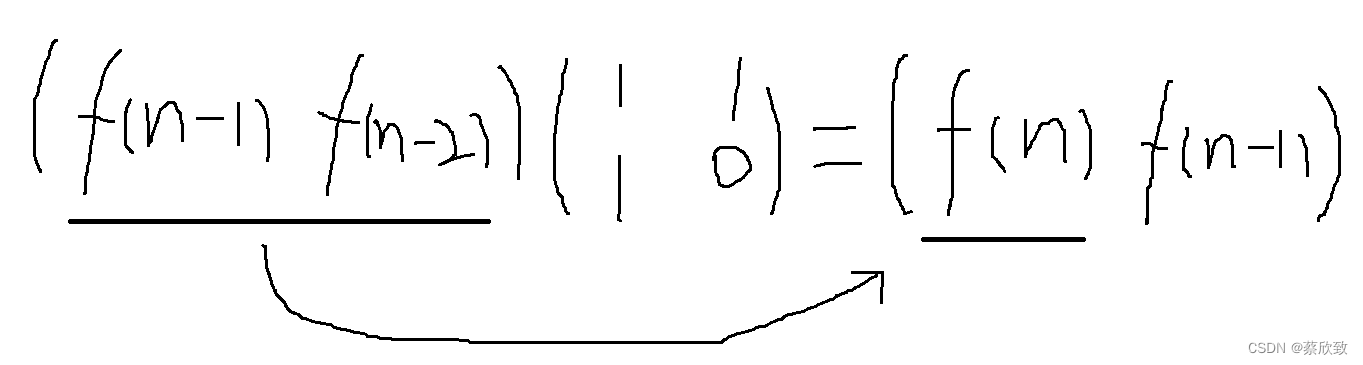什么是斐波那契数列,1,1,2,3,5,8,13...这样一个数列就是斐波那契数列,求第n项的值。
一、经典求法
观察数列可得,除了第一项和第二项,所有的数列的值都是前一项和前一项的前一项的加和,转换成函数也就是f(n) = f(n-1) + f(n-2)
public static int f1(int n) {if(n < 1) {return 0;}else if(n == 1 || n == 2) {return 1;}return f1(n-1) + f1(n-2);
}显然,递归n次,时间复杂度O(2^n),太恐怖,所以,必须优化。
二、顺序求法
因为斐波那契数列可以从左到右顺序的求出每一项的值,因此只需要顺序计算到n项即可,时间复杂度为O(n)的,我们可以把它看成在单链表的最后插入一个右最后一个和倒数第二个指针指向的值来决定的。
public static int f2(int n) {if(n < 1) {return 0;}else if(n == 1 || n == 2) {return 1;}int res = 1;int pre = 1;int temp = 0;for(int i = 3; i < n; i++) {temp = res;res = pre + res;pre = temp;}return res;}
三、状态矩阵相乘求法
这是一个时间复杂度为O(log n)的算法。因为斐波那契数列在n大于等于三的时候严格遵守递推数列f(n) = f(n-1) + f(n-2),而对于一个二阶的递推数列来说,我们可以用矩阵乘法来表示,且状态矩阵是2阶的方阵:

(F(N),F(N-1))= (F(N-1),F(N-2))*A
这个矩阵是怎么得到的呢,其实回顾一下我们所学的遇到一个递推公式,如何求通项公式的问题,是不是就是构造一个等比数列啊,然后换元累加求解,举个例子,温习一下:
---------------------------------------------------------------------------------------------------------------------
使用特征方程计算:
可以看到,这两种方法计算的结果相同,且都是正确的,但使用特征方程求解,十分方便.使用特征方程的一个问题是,如何计算得到递推公式的特征方程,
如上图,计算一个递推公式的通项公式,只要将c1和c2的值带入r^2 = c1 * r + c2即可,然后用上述的方法求解通项公式即可.注意,上述方法仅针对
这种形式的递推公式.
原理解决,下面继续看具体求法:
----------------------------------------------------------------------------------------------------------------------
把斐波那契数列的前四项F(1) = 1、F(2) = 1、F(3) = 2、F(4) = 3带进去可得状态矩阵的为:
当求出状态矩阵之后,当n >= 2时,原来的公式可简化为:
(F(3),F(2))= (F(2),F(1))*A = (1,1)*A
(F(4),F(3))= (F(3),F(2))*A = (1,1)*A^2
.....
(F(N),F(N-1))= (F(N-1),F(N-2))*A = (1,1) *A^(n-2)
所以其斐波那契数列n项和的问题就转化为如何用一个最快的方法求一个矩阵的N次方的问题,而求矩阵N方的问题显然能够在O(log n)时间内解决的问题,因为一个矩阵的实质其实就是一个值,假设这个数为a,如何快速的求a^75次幂的值,因为75次幂的二进制形式为1001011,那么a^75就可以写成a^64*a^8*a^2*a^1,在这过程中,我们先求出a的一次幂,再求2次幂,在根据2次幂去求4次幂以此类推,最后根据32次幂求出64次幂,即75的二进制形式共有多少位我们就使用了几次乘法,而且只乘相位上为1的位置即可。
代码实现:
//特征矩阵法//求矩阵m的p次幂的值public static int[][] matrixPower(int[][] m, int p){int [][] res = new int[m.length][m[0].length];//先把res设为单位矩阵,相当于整数中的1for (int i = 0; i < res.length; i++) {res[i][i] = 1;}//临时矩阵int [][] tmp = m;for (; p != 0; p >>= 1) {if ((p & 1) != 0) {//按位与操作,其实也就是位置为1的乘把这个矩阵乘一下res = muliMatrix(res, tmp);}//等于0 的时候我临时矩阵自己乘一下tmp = muliMatrix(tmp, tmp);}return res;}//两矩阵相乘public static int[][] muliMatrix(int[][] m1, int[][] m2) {//构造出一个m1行和m2列的矩阵(矩阵相乘规则)int [][] res = new int[m1.length][m2[0].length];//给我们要得到的矩阵的每一个元素的值进行赋值操作for(int i = 0; i < m1.length; i++) {for(int j = 0; j < m2[0].length; j++) {for(int k = 0; k < m2.length; k++) {//i,j位置元素的值就是i行元素和j行元素乘积的加和res[i][j] += m1[i][k] * m2[k][j];}}}return res;}//利用矩阵乘法求解斐波那契数列第n项的值public int f3(int n){if(n < 1) {return 0;}else if(n == 1 || n == 2) {return 1;}//状态矩阵int[][] base = {{1,1},{1,0}};//最后的结果需要求矩阵的n-2次int [][] res = matrixPower(base, n-2);return res[0][0] + res[1][0];}