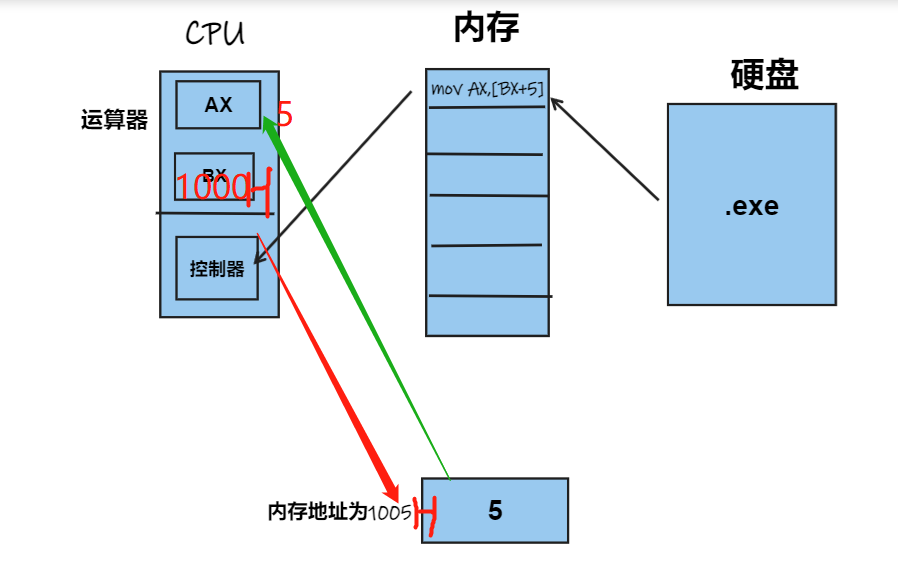
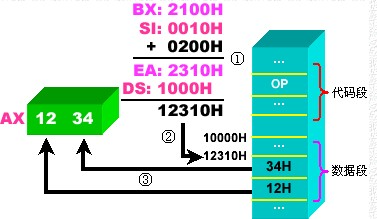
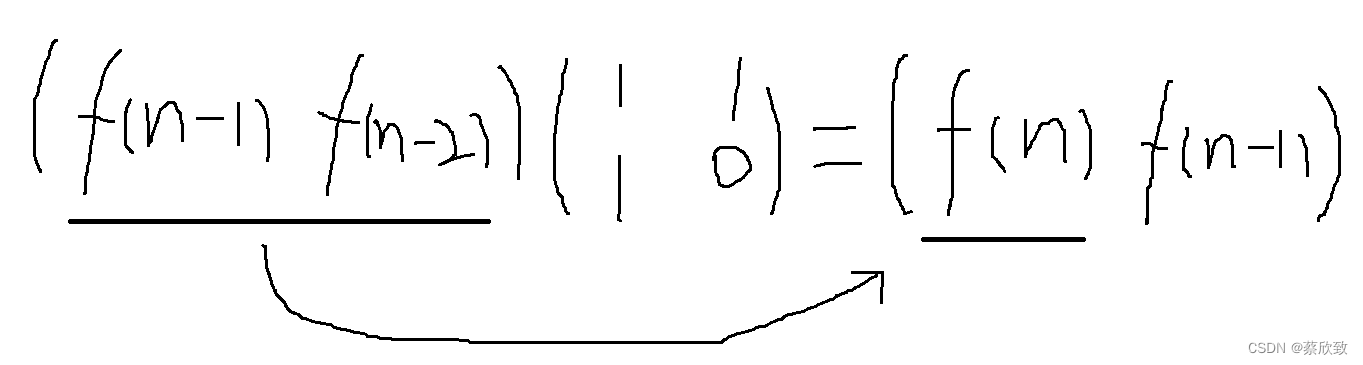斐波那切数列我们并不陌生。在百度百科中我们可以找到有关它的定义：斐波纳契数列（Fibonacci Sequence），又称黄金分割数列，指的是这样一个数列：1、1、2、3、5、8、13、21、……在数学上，斐波纳契数列以如下被以递归的方法定义：F0=0，F1=1，Fn=F(n-1)+F(n-2)（n>=2，n∈N*）。

斐波那切数列的通项公式为：

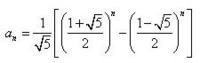
我们甚至可以找到它的几个应用：

1.有一段楼梯有10级台阶，规定每一步只能跨一级或两级，要登上第10级台阶有几种不同的走法?
解决：登上第一级台阶有一种登法；登上两级台阶，有两种登法；登上三级台阶，有三种登法；登上四级台阶，有五种登法……
1，2，3，5，8，13……所以，登上十级，有89种走法。

2.一枚均匀的硬币掷10次，问不连续出现正面的可能情形有多少种？

解决：掷一次有2种情况，掷二次有3种情况，掷三次有5种情况...掷10次有144种情况。

3.当n趋于无穷大时，F(n)/F(n+1）的极限是多少？　　

解决：这个可由它的通项公式直接得到，极限是（-1+√5)/2，这个就是黄金分割的数值，也是代表大自然的和谐的一个数字。

接下来我们来探讨一下斐波那切数列的一些解决算法：

1.递归算法（是最普遍的解决算法）

int fib(int n)
{if(n<=1){return n;}else{return fib(n-1) + fib(n-2);}}

这种算法的时间复杂度很高。因为在计算fib(n-1)的时候，把fib(n-2)也给计算了一遍。这样资源得不到重复利用。时间复杂度是指数级的。

2.非递归算法（迭代法）

int fib(int n)
{int a=0;int b=1;int c;for(int i=2;i<=n;i++){c = a + b;a = b;b = c;}return c;}

这个算法实际上是根据概念走的。比较简单。另外如果想要提高效率，其实可以将三个变量变为两个变量来做：

int fib(int n)
{int a=0;int b=1;for(int i=2;i<=n;i++){b = a + b;a = b-a;}return b;}

3.矩阵运算：

矩阵运算是能使算法的时间复杂度达到O(logn)的算法，其主要的思路如下：

现在我们主要要知道如何求：。我们可以采用分治法，具体来讲是二分法来解决这个问题：

这样我们容易写出代码：

//定义2×2矩阵；
struct Matrix2by2
{//数据成员int m00;int m01;int m10;int m11;//构造函数Matrix2by2(int m_00,int m_01,int m_10,int  m_11){m00 = m_00;m01 = m_01;m10 = m_10;m11 = m_11;}};//定义2×2矩阵的乘法运算
Matrix2by2 MatrixMultiply(const Matrix2by2& matrix1,const Matrix2by2& matrix2)
{Matrix2by2 matrix12(1,1,1,0);matrix12.m00 = matrix1.m00 * matrix2.m00 + matrix1.m01 * matrix2.m10;matrix12.m01 = matrix1.m00 * matrix2.m01 + matrix1.m01 * matrix2.m11;matrix12.m10 = matrix1.m10 * matrix2.m00 + matrix1.m11 * matrix2.m10;matrix12.m11 = matrix1.m10 * matrix2.m01 + matrix1.m11 * matrix2.m11;return matrix12;}//定义2×2矩阵的幂运算
Matrix2by2 MatrixPower(unsigned int n)
{Matrix2by2 matrix(1,1,1,0);if (n == 1){matrix = Matrix2by2(1,1,1,0);}else if (n % 2 == 0){matrix = MatrixPower(n / 2);matrix = MatrixMultiply(matrix, matrix);}else if (n % 2 == 1){matrix = MatrixPower((n-1) / 2);matrix = MatrixMultiply(matrix, matrix);matrix = MatrixMultiply(matrix, Matrix2by2(1,1,1,0));}return matrix;
}
//计算Fibnacci的第n项
int fib(unsigned int n)
{if (n == 0)return 0;if (n == 1)return 1;Matrix2by2 fibMatrix = MatrixPower(n-1);return fibMatrix.m00;}

4.公式法：

根据这个公式就可以求出第N项，具体代码就不给出了。

5.表驱动的递归法：

这个方法其实是利用递归法的缺点加以改进，在已经计算过的f(n)，就不必重复计算了。

#define MAX_LOG 20
int Logs[MAX_LOG] = {0};
int fib(int n)
{if (n <= 1) {return n;} else if (n < MAX_LOG && Logs[n] != 0) {return Logs[n];} else {Logs[n] = fib(n - 1) + fib(n - 2);return Logs[n];}
}

但是在N很大的情况下，不太适用。

6.变形的递归程序。。其实就是迭代法的变形，只不过将while循环或者是for循环的部分变成了递归而已。

int fib_2(int n ,int a ,int b,int count)
{if(count == n) return b;return fib(n,b,a+b,++count);
}
int fib(int n)
{return fib_2(n,0,1,1);
}