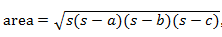三角形面积的两种求法

1、已知三顶点坐标求三角形面积

对于两个列向量(x1， y1)和(x2， y2)，我们将上述两个向量合并形成一个2*2的矩阵，当前矩阵的行列式就等于这两台向量所围成的平行四边形的面积，三角形的面积就是当前平行四边形面积的一半。

| x1 x2|
| y1 y2|

假如两个向量分别为(0, 1) (2, 1), 那么这两个向量形成的矩阵的行列式为2*1-1*0 , 结果等于2，也就是当前平行四边形的面积，因此三角形的面积就是1。
当我们知道三角形的三个点之后，我们就可以将其中的两条边的向量求出来，然后根据这两条向量直接求出三角形的面积。化简后公式如下：

三角形顶点:（x1, y1), (x2, y2), (x3, y3）
面积公式：S=(1/2)*(x1y2+x2y3+x3y1-x1y3-x2y1-x3y2)

代码如下：

#include <iostream>
#include <cmath>using namespace std;//S=(1/2)*(x1y2+x2y3+x3y1-x1y3-x2y1-x3y2)int main(){float num[6];for(int i = 0; i < 6; i++)cin >> num[i];float sum = 0.0;sum = 0.5*(num[0]*num[3]+num[2]*num[5]+num[4]*num[1]-num[0]*num[5]-num[2]*num[1]-num[4]*num[3]);cout << "三角形的面积为: ";sum == 0 ? cout << "Imposiible" : cout <<sum;return 0;
}

2、已知三边长求三角形面积

以下是百度百科关于海伦公式的介绍图片：

百度百科关于海伦公式的图片
代码如下：

#include <iostream>
#include <cmath>using namespace std;int main(){double a, b, c, p, sum;cin >> a>> b>> c;p=(a+b+c)/2;sum=sqrt(p*(p-a)*(p-b)*(p-c));cout << "三角形的面积为: ";sum == 0 ? cout << "Imposiible" : cout << sum;return 0;
}