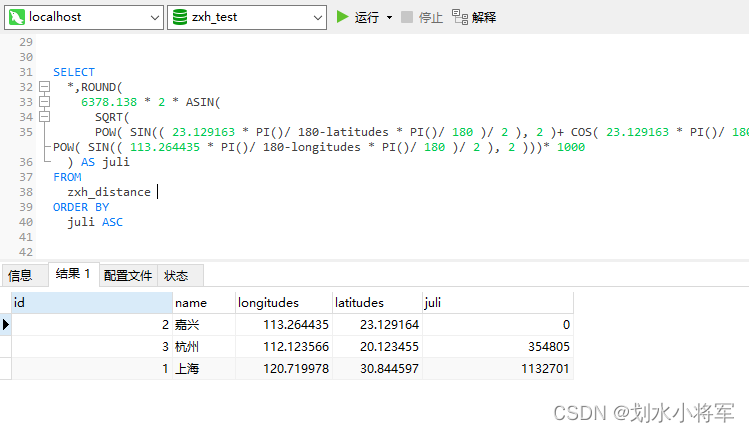
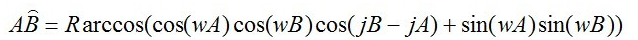根据两个经纬度点计算距离

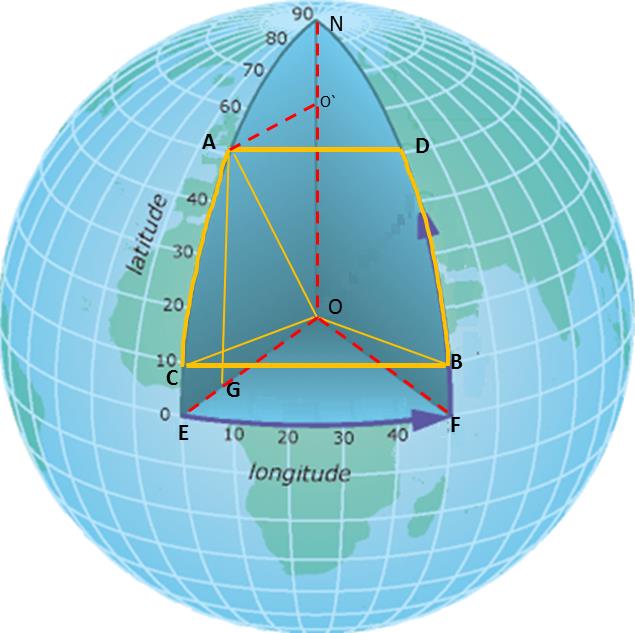
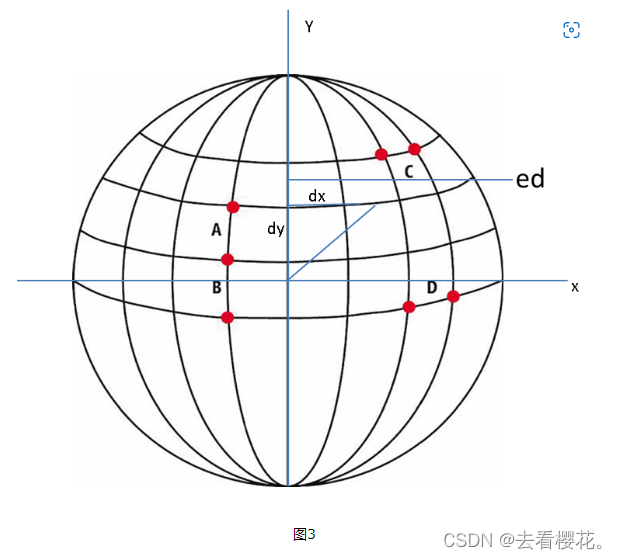
假设要算的距离为A、B两点之间的距离，A、B两点的经线相交于南北极，纬线平行，找出C点和B点同一条纬线和A点同一条经线，同理找出D点。这时如果想要知道A和B距离只要知道角AOB的角度再根据求弧长的公式即可得出。现在问题简化为求角AOB，O为地球球心到表面四个点的长度都是地球半径。所以我们求出AB的直线距离就可以求出角AOB的度数。这时我们可以把它简化为平面等腰梯形求对边的长度了。

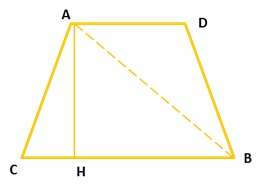
推导过程：

维度（0-90）：lat1,lat2
经度（0-180）：lon1,lon2
维度差：dlat = lat1 -lat 2;
精度差: dlon = lon1 - lon2;
地球半径：r
角AOC的值为维度差
角AOD和角COB的值为经度差 
AC = 2*r*sin(dlat/2);
AO'= COS(lat1)*r;
AD = 2*AO'*sin(dlon/2) = 2*COS(lat1)*r*sin(dlon/2);
CB = 2*COS(lat2)*r*sin(dlon/2);
CH = (CB - AD)/2;
AH^2 = AC^2 - CH^2
HB = CB - CH;
AB = AH^2 + HB^2;
化简可得
AB^2 = AC^2 + CB*AD=4*r*r*sin(dlat/2)^2 + 2*COS(lat2)*r*sin(dlon/2)*2*COS(lat1)*r*sin(dlon/2);
AB = 2*r*sqrt(sin(dlat/2)^2 + COS(lat2)*COS(lat1)*sin(dlon/2)^2);
h = r*sqrt(sin(dlat/2)^2 + COS(lat2)*COS(lat1)*sin(dlon/2)^2); // 弦AB的一半
sin（AOB/2） = h/r = sqrt(sin(dlat/2)^2 + COS(lat2)*COS(lat1)*sin(dlon/2)^2) //	角AOB一半的正弦值
d_rad = 2 * asin(h/r) = asin(sqrt(sin(dlat/2)^2 + COS(lat2)*COS(lat1)*sin(dlon/2)^2)); //角AOB之间的角度
d = d_rad * r;

程序

#include <stdio.h>
#include <math.h>/********弧度计算公式*********/
double earth_rad (double w_rad)
{const double pi = 3.1415926535898;return (pi*w_rad)/180;
}/********经纬度距离计算公式*********/
//lon:经度
//lat:维度
//返回值单位为 m
double get_distance (double lon1, double lat1, double lon2, double lat2)
{const double radius = 6378.137;double dlat = earth_rad(lat2) - earth_rad(lat1);          //维度差double dlon = earth_rad(lon1) - earth_rad(lon2);          //经度差double r_lat1 = earth_rad(lat1);double r_lat2 = earth_rad(lat2);double sindlat = sin(dlat/2)*sin(dlat/2);double sindlon = sin(dlon/2)*sin(dlon/2);double harve = 2 * asin(sqrt(sindlat + cos(r_lat1)*cos(r_lat2)*sindlon));return harve * radius * 1000;
}