---

前言

Traffic morphing是一种流量混淆方法，原作者采用凸优化技术将源流量侧信道的特征更改为另一种目标流量的侧信道特征来阻止流量分析攻击。

---

1 变形

变形的目的是为加密用户提供一种有效的方法来防止信息泄露，该方法比传统的填充法开销要小得多。要求是模仿目标流量、尽量降低开销、并且保证实时性。

1.1 符号表示及算法讲解

1.1.1 符号

源流量：$X=[x_1,x_2,...,x_n{]}^T$, $X_i$是源流量中第i大数据包长度的概率。
目标流量：$Y=[y_1,y_2,...,y_n{]}^T$，$Y_i$是目标流量中第i大数据包长度的概率。
变形矩阵：$A=[a(ij)]$，其中a(ij)表示将源流量只不过第j大的数据包长度$S_j$变为目标流量中第i大的数据包长度$d_i$的概率。变形矩阵A采用凸优化技术求出。当变形算法接收到大小为Sj的数据包时，算法会根据变形矩阵A中的概率分布采样，改变数据包大小以匹配$d_i$。
采样：将概率求和获得$S_j$转换为$d_1,d_2,...,d_n$的概率分布函数，算法先进行伪随机数r∈[0,1]采样，并以累积概率中第一个≥r的$d_i$为目标。步骤如下：

• 先求得$F=P(s_j\le d_i)，i\in [1,n]$
• 按随机分布生成随机数$r\in [0,1]$
• 选择$P(s_j\le d_k)\ge r，且P(s_j<=d_k-1)$
• 若通过以上采样得到的$d_k\ge s_j$，则填充源数据至$d_k$
• 若通过以上采样得到的$d_k＜s_j$，则将源数据包分片

1.1.2 凸优化求解

变形公式为Y=AX，展开后如下:

从上可得：$y_i=a_{i1}{x}_1+a_{i2}{x}_2+...+a_{in}{x}_n$
其中$a_{i1}+a_{2j}+...+a_{nj}=1$时等式才有意义，因为$a_{1j}$表示的是$x_j$有$a_{1j}$的概率转换为$y_1$，$a_{2j}$表示的是$x_j$有$a_{2j}$的概率转换为$y_2$，以此类推。
又因为变形会带来开销，变形技术的目标之一是尽量降低开销，所以定义成本函数如下：
$f_0(A)={\sum }_{i,j\in [1,n]}{x}_j{a}_{ij}(|di-sj|)]={\sum }_j^n{\sum }_i^n{x}_j{a}_{ij}(|d_i-s_j|)$
其中，$d_i$为目标数据包长度，$s_j$为源目标数据包长度

综上，该优化问题可写为：
$minimize{f}_0(A)$

约束：
${\sum }_{j=1}^n{a}_{ij}{x}_j=y_i,i\in [1,n]$
${\sum }_{i=1}^n{a}_{ij}=1,i\in [1,n]$
$a_{ij}\ge 0,i\in [1,n]j\in [1,n]$

1.1.3 降低开销

为了减少分片，降低开销，可以将$d_i<s_j$的所有变形概率都指定为0，但是直接指定为0可能会导致变形效果不佳，因此开销和变形效果需要进行折衷。该论文提出了一个多级规划的方法来解决以上问题，思想是找一个满足所有约束的矩阵$A^{\prime }$，使得$Z=A^{\prime }X$，其中Z是非常接近于原目标分布Y的，但由X变为Z满足去掉所有可能产生分片的情况。

由此可以进一步得到一个新的凸优化问题求解如下：
$minimize{f}_d(Y,Z)$

约束：
$Z=A^{\prime }X$
${\sum }_{i=1}^n{a}_{ij}^{\prime }=1,j\in [1,n]$
$a_{ij}^{\prime }>0,i、j\in [1,n]$
$a_{ij}^{\prime }=0,d_i<s_j$

此外，原有的凸优化问题也需要继续求解：
$minimize{f}_0(A)$

约束：
${\sum }_{j=1}^n{a}_{ij}{x}_j=z_i,i\in [1,n]$
${\sum }_{i=1}^n{a}_{ij}=1,j\in [1,n]$
$a_{ij}\ge 0,i、j\in [1,n]$
$a_{ij}=0,d_i＜s_j$

1.1.4大样本空间分治

如果变形矩阵大小为1460x1460（1460是最大报文长度），则会产生非常多的约束，在求解变形矩阵的时候产生巨大的开销。具体产生的开销有多大可以看下原文，原文进行了详细的描述。

因此为了解决大样本空间开销大的问题，论文作者将n各大空间划分为m个小分区，每个分区大小为$n/m$，然后到处m个输入分区到m各输出分区的粗变形矩阵。

分治的好处就在于将一个难以求解的大问题转化为了一个个易于求解的小问题，在该论文里面具体来说就是将$n\ast n$的X变形为Y的问题，转化为$m\ast m$的X’变形为Y’的问题。

$X^{\prime }=[X_1^{\prime },X_2^{\prime },...,X_m^{\prime }]$，$Y^{\prime }=[Y_1^{\prime },Y_2^{\prime },...,Y_m^{\prime }]$，其中$X_1^{\prime }$是原来X向量中的$[X_1,X_2,...,X_{n/m}]$的中位数或平均数或其他能代表该区间的数，总之$X_i^{\prime }$代表的是一个区间，同理$X_i^{\prime }$也是。

然后可以继续将$X_i^{\prime }$与$Y_i^{\prime }$继续往下分区，直到一个区间的数量小到便于求解为止。

1.1.5实验中的注意事项

短会话

该论文提出的方法适用于大量数据包生成的场景，大部分视频、音频类的流量包还是比较多的，但有些服务产生的流量包较少。解决方法是让整个变形效果与原目标流量相似度达到一定程度后终止变形，然后直接从目标流量中采样产生数据包，直到相似度达到一个阈值。

源分布变化多样

如果源分布具有明显的差异性，则变形方法性能会有所下降，解决方法是采用粗粒度的变形矩阵，同上述1.1.4中所说的分治产生的粗粒度变形矩阵类似，但是不会继续往下产生更细致的确定的变形子矩阵。也就是说，将源流量和目标流量包大小按分区划分，计算源流量包大小，各分区到目标流量包大小各分区的粗变形矩阵。每次仅限变形时，先计算源流量所属的分区A，然后根据粗变形矩阵进行采样，得到目标流量分区B，再在分区B中直接按目标流量包大小分布进行采样得到最终要变形的目标包大小$d_i$，最后再将$s_j$变形为$d_i$，由此完成变形。

数据包分片

如果目标流量大小$d_i$＜源包大小$s_j$，源包就需要进行分片，处理流程是将$s_j$大小的包分为$d_i$和$s_j-d_i$大小的两个包，$s_j-d_i$不再计算其变形矩阵，因为$s_j-d_i$的先验概率难以获取。所以直接对目标分布采样得到$s_j-d_i$的应变形的包长。需要注意的是，有可能一次分片不能解决问题，这样就需要多次分片，直到所有数据发送完成。

2 实验评估

为了验证方法的有效性，该论文设计了两个实验。

2.1 加密IP语音识别

实验将CSLU的"22 Language"电话音频作为分类数据集，采用Language Identification of Encrypted VoIP Traffic: Alejandra y Roberto or Alice and Bob?论文中提出的分类方法对该数据集进行分类，变形的目的就是降低该分类器的效果，变形方法有两类，其一是白盒变形，其二是黑盒变形。

白盒变形

在编码解码器中修改语音比特率以修改数据包大小

黑盒变形

对编码解码器一无所知，直接对流量包进行变形，但不允许进行分片

2.1.1 与原始分类器对抗

在Language Identification of Encrypted VoIP Traffic: Alejandra y Roberto or Alice and Bob?一文中有两种分类器，分别是二元分类器和三元分类器（这里因为没有看该论文，所以我也不是很了解这两种分类器，只从Traffic morphing中知道三元分类器效果要比二元分类器效果好）

二元分类器

原性能：平均准确率为71%
黑盒变形后：平均准确率45%
白盒变形后：平均准确率30%

三元分类器

原性能：平均准确率76%
黑盒变形后：平均准确率45%
白盒变形后：平均准确率38%

2.1.2 不可区分性评估

该实验的目的是查看已变形流量和目标流量是否具有不可区分性。
猜想：若变形完美，则分类器无法区分上述两类流量，分类器的平均准确率应为50%
结果：如下图所示，对于二元分类器无法区分变形流量与正常流量；对于三元分类器不可区分性比二元分类器差一些。

2.2 网页识别

Inferring the Source of Encrypted HTTP Connections一文中提出的网页分类器仅使用包大小和传播方向即可识别加密下载的网页。

2.2.1 与原始分类器的对抗

原始分类器：平均准确率98.4%
变形后：平均准确率为4.5%
效果如下图所示

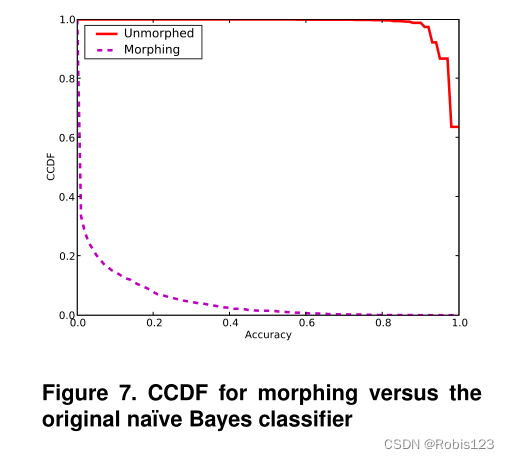
2.2.2 不可区分性评估

变形方法获得的不可区分性：以38.9%的开销实现了63.4%的准确度
填充方法获得的不可区分性：以4.5%的开销实现了86.2%的准确度

2.3 讨论

根据上述两个实验可知，Traffic morphing提出的变形方法比确定性填充减少了开销，同时增强了用户隐私性。

---

总结

总的来说，作者针对之前流量混淆方法（主要是填充法）的不足——开销大且易于识别，提出了一种新的流量变形技术，该方法将源流量侧信道特征变形为目标流量侧信道特征，以避免基于侧信道信息的流量分析攻击。
这个方法虽然是比较09年提出了，但到现在仍然还有很多文章引用他，我认为原因主要有两个，其一是这个方法是流量模仿的第一篇，其二是这篇论文之后没有更好的流量模仿的论文了。