倾斜补偿的电子罗盘(3):椭球拟合,磁传感器软磁干扰和硬磁干扰的9参数校准
背景
之前提到磁传感器的误差来源,并介绍了消除硬磁干扰的3参数校准。倾斜补偿的电子罗盘(2):磁传感器的误差来源、硬磁干扰的校准(3个参数)、实验验证
硬磁干扰的影响相当于零偏,导致数据点所在的球面发生平移。而软磁干扰会导致球面变为椭球,如下图,同时存在硬磁和软磁干扰的情况:
Layout Recommendations for PCBs Using a Magnetometer Sensor (nxp.com.cn)
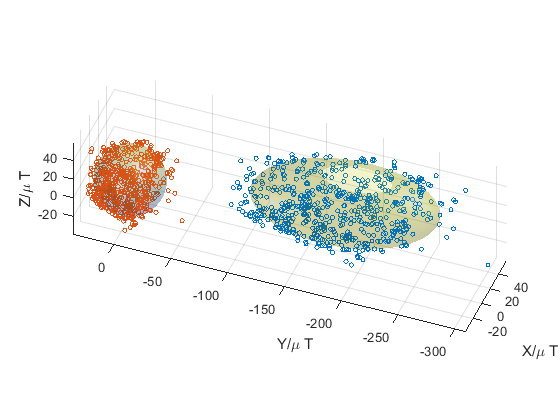
同样,获得磁传感器读数后,需要通过校准消除软磁和硬磁干扰的影响,校准后的数据然后再用于后续处理实现电子罗盘功能,见 倾斜补偿的电子罗盘(1):地磁场,磁传感器,倾斜补偿
电子罗盘使用中的校准流程:
- 进行一次任意旋转,尽量包含多个方向,使得拟合更准确(比如手机的指南针应用,启动后有时需要把手机旋转几次才能继续使用,可能就是这个原因?)
- 用获得的数据进行拟合,根据拟合结果计算 W − 1 \mathbf{W}^{-1} W−1和 V \mathbf{V} V
- 对于新获得的读数 h \mathbf{h} h,用 h 0 = W − 1 ( h − V ) \mathbf{h_0} = \mathbf{W^{-1}}(\mathbf{h}-\mathbf{V}) h0=W−1(h−V)进行校准,然后基于 h 0 \mathbf{h_0} h0可以使用倾斜补偿来获得方位
本文介绍计算 W − 1 \mathbf{W}^{-1} W−1和 V \mathbf{V} V的过程,并用样机做了校准+倾斜补偿的测试。
这里只是跟着参考资料操作了拟合的每个步骤,但是对于椭球拟合部分具体的原理其实不太理解(好久没接触线代了),不过看起来效果还不错。
椭球拟合
椭球的表达式
首先,椭球面表达式:
h 0 T h 0 = [ W − 1 ( h − V ) ] T W − 1 ( h − V ) = B 2 \mathbf{h_0^T}\mathbf{h_0} = [\mathbf{W}^{-1}(\mathbf{h}-\mathbf{V})]^T\mathbf{W}^{-1}(\mathbf{h}-\mathbf{V})=B^2 h0Th0=[W−1(h−V)]TW−1(h−V)=B2
其中, W − 1 \mathbf{W}^{-1} W−1是对称矩阵。
展开后:
h T ( W − 1 ) T W − 1 h − 2 h T ( W − 1 ) T W − 1 V + V T ( W − 1 ) T W − 1 V − B 2 = 0 → h T M h + 2 h T n + d = 0 \mathbf{h}^T(\mathbf{W}^{-1})^{T}\mathbf{W}^{-1}\mathbf{h}-2\mathbf{h}^T(\mathbf{W}^{-1})^{T}\mathbf{W}^{-1}\mathbf{V} +\mathbf{V}^T(\mathbf{W}^{-1})^{T}\mathbf{W}^{-1}\mathbf{V}-B^2=0 \\ \rightarrow \mathbf{h}^T\mathbf{M}\mathbf{h}+2\mathbf{h}^T\mathbf{n}+d=0 hT(W−1)TW−1h−2hT(W−1)TW−1V+VT(W−1)TW−1V−B2=0→hTMh+2hTn+d=0
其中,
M = ( W − 1 ) T W − 1 = ( W − 1 ) 2 n = − M V d = V T M V − B 2 \mathbf{M} = (\mathbf{W}^{-1})^{T}\mathbf{W}^{-1} = (\mathbf{W}^{-1})^2 \\ \mathbf{n} = -\mathbf{M} \mathbf{V} \\ d = \mathbf{V}^T\mathbf{M}\mathbf{V}-B^2 M=(W−1)TW−1=(W−1)2n=−MVd=VTMV−B2
同时,用xyz表示:
a x 2 + b y 2 + c z 2 + 2 f y z + 2 g x z + 2 h x y + 2 p x + 2 q y + 2 r z + d = v T x = 0 , v = [ a b c f g h p q r d ] T x = [ x 2 y 2 z 2 2 y z 2 x z 2 x y 2 x 2 y 2 z 1 ] T ax^2+by^2+cz^2+2fyz+2gxz+2hxy+2px+2qy+2rz+d=\mathbf{v}^T\mathbf{x}=0, \\ \mathbf{v} = \left[ \begin{matrix} a &b &c &f &g &h &p &q &r &d \end{matrix} \right]^T \\ \mathbf{x} = \left[ \begin{matrix} x^2 &y^2 &z^2 &2yz &2xz &2xy &2x &2y &2z &1 \end{matrix} \right]^T ax2+by2+cz2+2fyz+2gxz+2hxy+2px+2qy+2rz+d=vTx=0,v=[abcfghpqrd]Tx=[x2y2z22yz2xz2xy2x2y2z1]T
则系数的对应关系为:
M = [ a h g h b f g f c ] , n = [ p q r ] \mathbf{M} = \left[ \begin{matrix} a &h &g\\ h &b &f\\ g &f &c \end{matrix} \right], \mathbf{n} = \left[ \begin{matrix} p \\ q \\ r \end{matrix} \right] M= ahghbfgfc ,n= pqr
椭球拟合实际上就是要获得 v \mathbf{v} v的10个系数。
简单验证系数的对应关系:
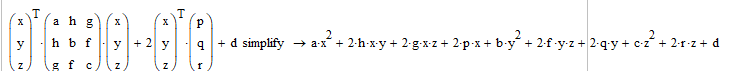
拟合过程
此处只介绍计算过程,也是基于最小二乘法,详见参考资料。
-
使用m组测量数据构建10*m矩阵 D = [ x 1 , x 2 , . . . , x m ] \mathbf{D}=[\mathbf{x_1},\mathbf{x_2},...,\mathbf{x_m}] D=[x1,x2,...,xm]。根据我们选用的模型,
a x 2 + b y 2 + c z 2 + 2 f y z + 2 g x z + 2 h x y + 2 p x + 2 q y + 2 r z + d = v T x = 0 ax^2+by^2+cz^2+2fyz+2gxz+2hxy+2px+2qy+2rz+d=\mathbf{v}^T\mathbf{x}=0 ax2+by2+cz2+2fyz+2gxz+2hxy+2px+2qy+2rz+d=vTx=0
需要获得一组 v \mathbf{v} v,实现 m i n ( ∣ ∣ D v ∣ ∣ 2 ) min(||\mathbf{D}\mathbf{v}||^2) min(∣∣Dv∣∣2)。后续的算法是把这个优化问题转化后再进行求解。(不太理解具体是怎么转化的。。) -
计算 S = D D T \mathbf{S}=\mathbf{D}\mathbf{D}^T S=DDT
-
对 S \mathbf{S} S和 v \mathbf{v} v进行分块:
S = D D T = [ ( S 11 ) 6 × 6 ( S 12 ) 6 × 4 ( S 12 ) 4 × 6 T ( S 22 ) 4 × 4 ] , v = [ ( v 1 ) 6 × 1 ( v 2 ) 4 × 1 ] \mathbf{S}=\mathbf{D}\mathbf{D}^T=\left[ \begin{matrix} (S_{11})_{6\times6} & (S_{12})_{6\times4}\\ (S_{12})^T_{4\times6} & (S_{22})_{4\times4}\\ \end{matrix} \right], \mathbf{v} = \left[ \begin{matrix} (\mathbf{v}_1)_{6\times1} \\ (\mathbf{v}_2)_{4\times1} \end{matrix} \right] S=DDT=[(S11)6×6(S12)4×6T(S12)6×4(S22)4×4],v=[(v1)6×1(v2)4×1]
-
直接计算 v 1 , v 2 \mathbf{v}_1,\mathbf{v}_2 v1,v2,优化问题被转化为:
( S 11 − λ C 1 ) v 1 + S 12 v 2 = 0 ( 1 ) S 12 T v 1 + S 22 v 2 = 0 ( 2 ) (S_{11}-\lambda C_1)\mathbf{v}_1 + S_{12}\mathbf{v}_2 = 0 \quad (1)\\ S_{12}^T\mathbf{v}_1 + S_{22}\mathbf{v}_2 = 0 \quad (2) (S11−λC1)v1+S12v2=0(1)S12Tv1+S22v2=0(2)
其中,
C 1 = [ − 1 1 − 1 0 0 0 1 − 1 1 0 0 0 1 1 − 1 0 0 0 0 0 0 − 4 0 0 0 0 0 0 − 4 0 0 0 0 0 0 − 4 ] C_1 = \left[ \begin{matrix} -1 & 1 & -1 & 0 & 0 & 0 \\ 1 & -1 & 1 & 0 & 0 & 0 \\ 1 & 1 & -1 & 0 & 0 & 0 \\ 0 & 0 & 0 & -4 & 0 & 0 \\ 0 & 0 & 0 & 0 & -4 & 0 \\ 0 & 0 & 0 & 0 & 0 & -4 \\ \end{matrix} \right] C1= −1110001−11000−11−1000000−4000000−4000000−4
根据(2), v 2 = − S 22 − 1 S 12 T v 1 \mathbf{v}_2=-S_{22}^{-1}S_{12}^T\mathbf{v}_1 v2=−S22−1S12Tv1,代入(1):
C 1 − 1 ( S 11 − S 12 S 22 − 1 S 12 T ) v 1 = λ v 1 C_1^{-1} (S_{11}-S_{12}S_{22}^{-1}S_{12}^T)\mathbf{v}_1 = \lambda \mathbf{v}_1 C1−1(S11−S12S22−1S12T)v1=λv1
从这个公式可以看出 v 1 \mathbf{v}_1 v1是矩阵 C 1 − 1 ( S 11 − S 12 S 22 − 1 S 12 T ) C_1^{-1} (S_{11}-S_{12}S_{22}^{-1}S_{12}^T) C1−1(S11−S12S22−1S12T)的特征向量。因此,求矩阵 C 1 − 1 ( S 11 − S 12 S 22 − 1 S 12 T ) C_1^{-1} (S_{11}-S_{12}S_{22}^{-1}S_{12}^T) C1−1(S11−S12S22−1S12T)的所有特征向量,选择最大特征值对应的特征向量,就得到了 v 1 \mathbf{v}_1 v1。(不太理解为什么是最大特征值对应的特征向量。。)
-
使用 v 1 \mathbf{v}_1 v1计算 v 2 \mathbf{v}_2 v2, v 2 = − S 22 − 1 S 12 T v 1 \mathbf{v}_2=-S_{22}^{-1}S_{12}^T\mathbf{v}_1 v2=−S22−1S12Tv1
-
获得 v = [ ( v 1 ) 6 × 1 ( v 2 ) 4 × 1 ] \mathbf{v} = \left[ \begin{matrix} (\mathbf{v}_1)_{6\times1} \\ (\mathbf{v}_2)_{4\times1} \end{matrix} \right] v=[(v1)6×1(v2)4×1]。
使用拟合数据进行校准
整理下之前的结果.
已获得 v \mathbf{v} v:
v = [ a b c f g h p q r d ] T \mathbf{v} = \left[ \begin{matrix} a &b &c &f &g &h &p &q &r &d \end{matrix} \right]^T v=[abcfghpqrd]T
原始数据满足: h 0 T h 0 = [ W − 1 ( h − V ) ] T W − 1 ( h − V ) = B 2 \mathbf{h_0^T}\mathbf{h_0} = [\mathbf{W}^{-1}(\mathbf{h}-\mathbf{V})]^T\mathbf{W}^{-1}(\mathbf{h}-\mathbf{V})=B^2 h0Th0=[W−1(h−V)]TW−1(h−V)=B2,展开化简后是 h T M h + 2 h T n + d = 0 \mathbf{h}^T\mathbf{M}\mathbf{h}+2\mathbf{h}^T\mathbf{n}+d=0 hTMh+2hTn+d=0。
其中,
M = ( W − 1 ) T W − 1 = ( W − 1 ) 2 n = − M V d = V T M V − B 2 \mathbf{M} = (\mathbf{W}^{-1})^{T}\mathbf{W}^{-1} = (\mathbf{W}^{-1})^2 \\ \mathbf{n} = -\mathbf{M} \mathbf{V} \\ d = \mathbf{V}^T\mathbf{M}\mathbf{V}-B^2 M=(W−1)TW−1=(W−1)2n=−MVd=VTMV−B2
M , n \mathbf{M},\mathbf{n} M,n和 V \mathbf{V} V的关系为:
M = [ a h g h b f g f c ] , n = [ p q r ] \mathbf{M} = \left[ \begin{matrix} a &h &g\\ h &b &f\\ g &f &c \end{matrix} \right], \mathbf{n} = \left[ \begin{matrix} p \\ q \\ r \end{matrix} \right] M= ahghbfgfc ,n= pqr
因此,把 M , n \mathbf{M},\mathbf{n} M,n转换为最终需要的 W − 1 , V , B \mathbf{W}^{-1},\mathbf{V},B W−1,V,B:
W − 1 = M 1 2 V = − M − 1 n B = V T M V − d \mathbf{W}^{-1} = \mathbf{M}^{\frac{1}{2}} \\ \mathbf{V} = -\mathbf{M}^{-1} \mathbf{n} \\ B = \sqrt{\mathbf{V}^T\mathbf{M}\mathbf{V}-d} W−1=M21V=−M−1nB=VTMV−d
实验验证
拟合结果
之前3参数校准时,YZ画图如下,Z轴方向上,有不少点在拟合的球之外。
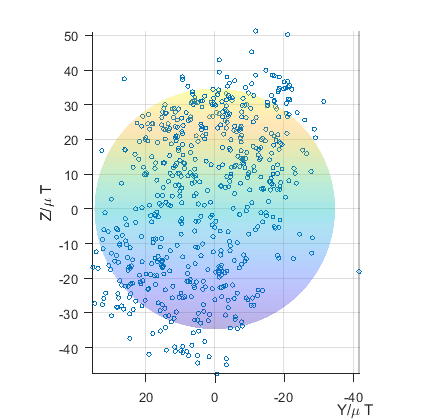
对同一组数据进行9参数校准,YZ画图,校准前后结果如下,用椭球拟合看起来效果更好一些。
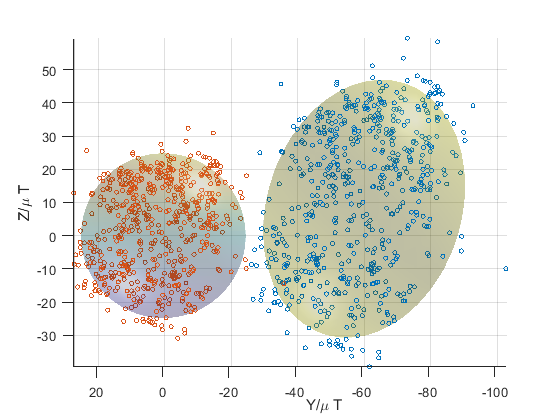
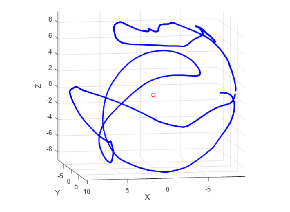
把Y轴原始数据乘以2,看下椭球拟合的效果。
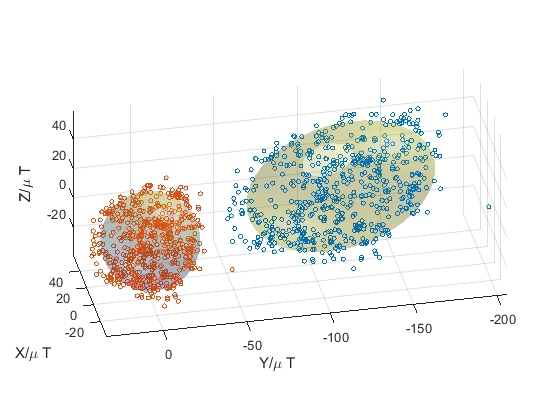
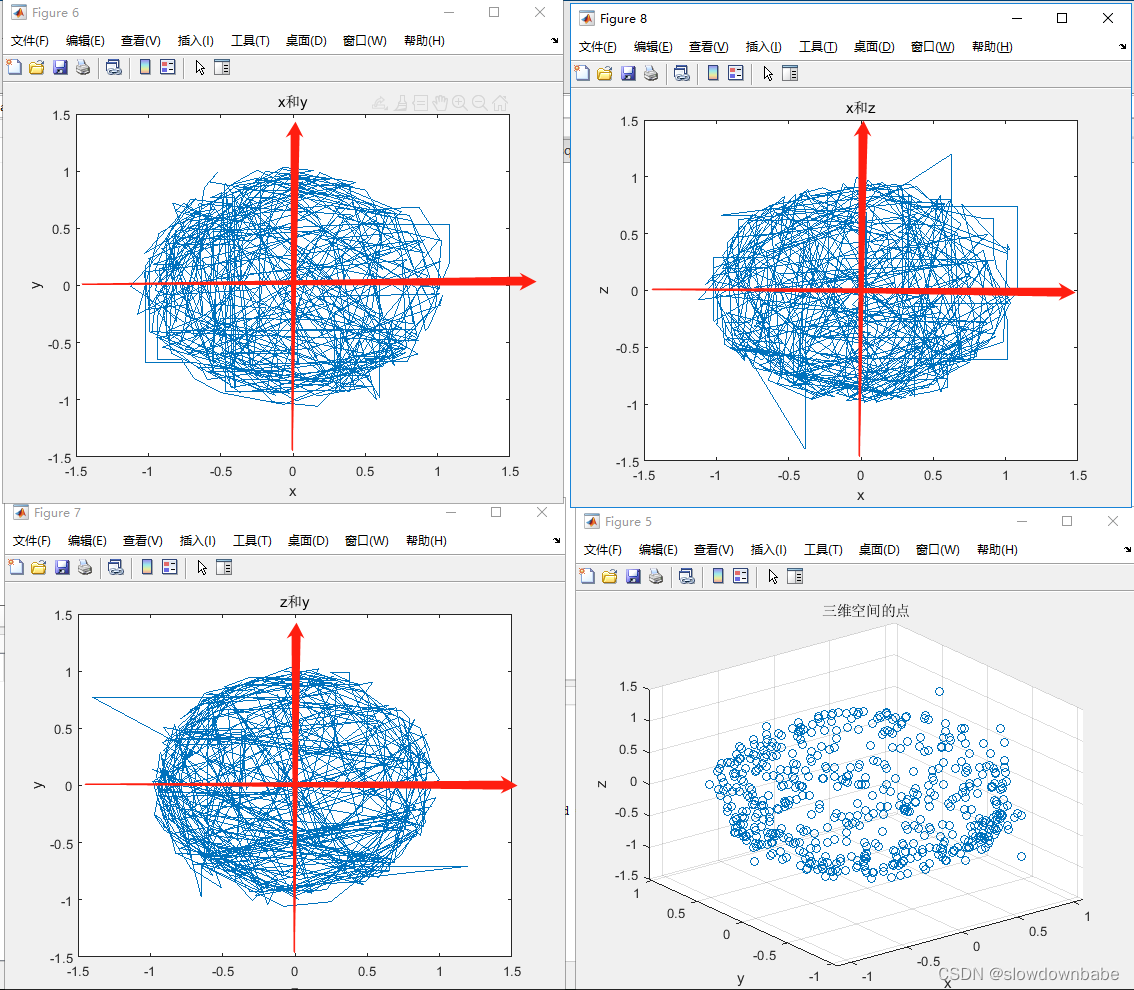
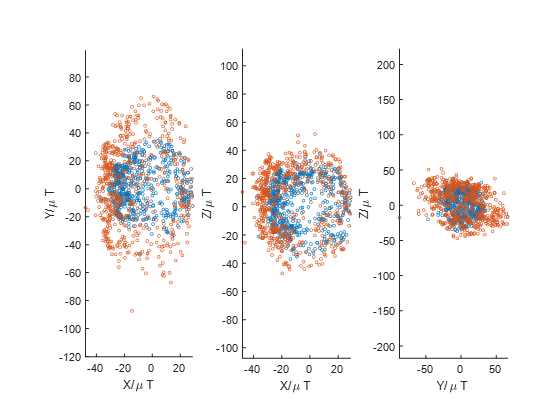
看下XY,XZ,YZ的数据:红色为校准前,蓝色为校准后,可见效果还不错。
校准实测
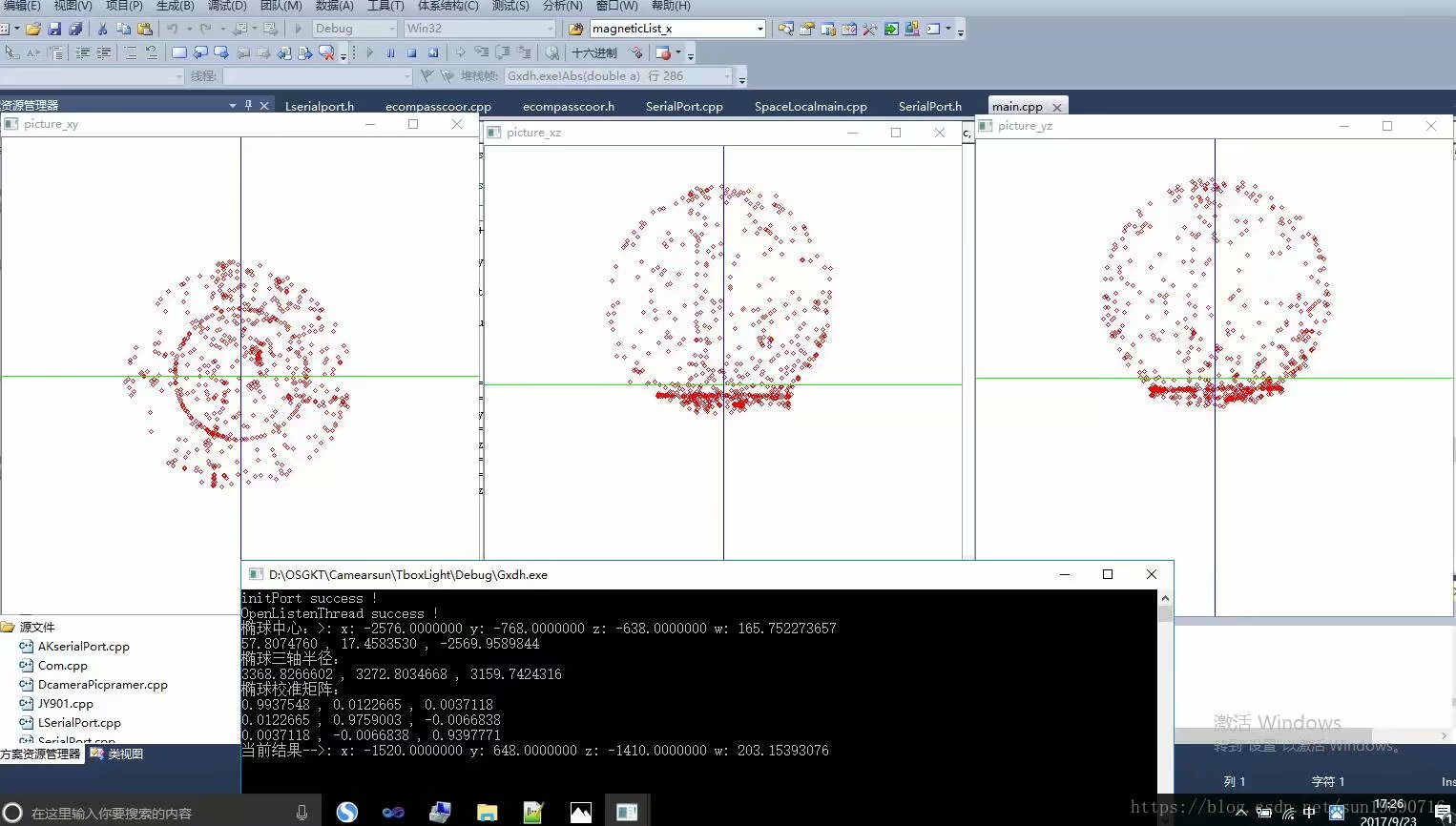
获得的 W − 1 , V \mathbf{W}^{-1},\mathbf{V} W−1,V数据:
W_inv = [ 0.7329 0.0389 -0.0044;0.0389 0.8484 -0.0151;-0.0044 -0.0151 0.6555];
V = [27.5424; -60.3430;9.6232];
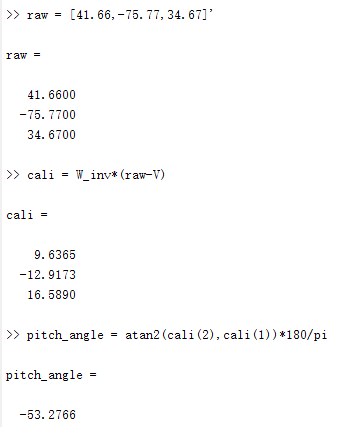
对于一组新的测量值raw = [41.66,-75.77,34.67]',计算如下:
- 先计算
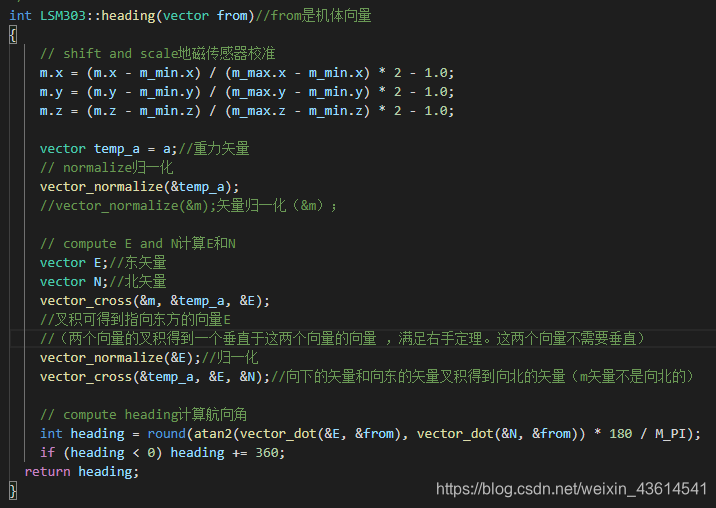
cali - 然后
atan2计算方位角为-53° - 按之前的定义(俯视,以磁北为基准,顺时针旋转为正,逆时针旋转为负),磁传感器的x轴与磁北的夹角为-53°,说明此时x轴是朝向北偏西53°。
参考资料
资料
软磁和硬磁干扰:Layout Recommendations for PCBs Using a Magnetometer Sensor (nxp.com.cn)
用了这篇文章的拟合方法:Least squares ellipsoid specific fitting | IEEE Conference Publication | IEEE Xplore
椭球拟合对应的matlab代码:Ellipsoid Fitting - File Exchange - MATLAB Central (Mathworks.cn)
椭球拟合+校准对应的python代码:Teslabs Engineering - A way to calibrate a magnetometer
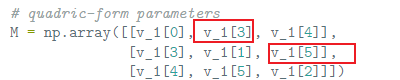
注意python代码中一个小错误:这个程序是完全按照文章中的方法计算的,在v和M的转换中,v_1[3]对应f,v_1[5]对应h,所以1,2和2,3这两项应该对调(同理,对称矩阵的另外两项2,1和3,2也要对调)。
代码
测量数据和完整代码在:电子罗盘磁传感器校准MATLAB代码(9参数椭球拟合)
以下是9参数拟合具体实现方法,是基于文献和参考链接的python修改而来的MATLAB代码:
D = [mag_x.^2, mag_y.^2, mag_z.^2, 2*mag_y.*mag_z, 2*mag_x.*mag_z, 2*mag_x.*mag_y, ...2*mag_x, 2*mag_y, 2*mag_z, ones(length(mag_x),1) ];
S = D' * D;
% 根据文章做分块
S11 = S(1:6, 1:6);
S12 = S(1:6, 7:10);
S21 = S(7:10, 1:6);
S22 = S(7:10, 7:10);% k=4
C = [-1, 1, 1, 0, 0, 0; 1, -1, 1, 0, 0, 0;1, 1, -1, 0, 0, 0;0, 0, 0, -4, 0, 0;0, 0, 0, 0, -4, 0;0, 0, 0, 0, 0, -4];M0 = inv(C) * (S11 - S12 * inv(S22) * S12');
[gevec, geval]=eig(M0); % M0 * gevec = gevec * geval%%% 以下是找唯一 正的特征值,对应的特征向量v1。
% geval是一个对角矩阵,diag(geval)返回的是主对角线的元素
% 找主对角线元素的最大值,和所在位置
[max_val, max_index] = max(diag(geval));
% 选择最大的特征值对应的特征向量
v1 = gevec(:,max_index);
if v1(1)<0 v1 = -v1;
end
% 这里有点看不懂了,v1为什么要取反?
% 但是如果不取反,M开根号后全是虚数了
v2 = - pinv(S22) * S12' * v1;% 还原M矩阵
M = [v1(1), v1(6), v1(5),;v1(6), v1(2), v1(4);v1(5), v1(4), v1(3)];
n = v2(1:3);
d = v2(4);% 获得最终需要的W^(-1)和V
V = - inv(M) * n;
W_inv = sqrtm(M);
B_est2 = sqrt(V'*M*V-d);data_raw = [mag_x, mag_y, mag_z]';
data_cali9 = zeros(size(data_raw));
% 对原始的每一组数据分别进行9参数校准
for i = 1:length(mag_x)h = data_raw(:,i);data_cali9(:,i) = W_inv * (h - V);
end