单因素方差分析的MATLAB实现


单因素均衡数据的实现





单因素非均衡数据方差分析
p192 8.22

X=[85,80,90,88,87,94,56,62,55,48,92,99,95,91,75,72,81];group=[ones(1,3),2*ones(1,4),3*ones(1,2),4*ones(1,2),5*ones(1,4),6*ones(1,3)];anova1(X,group);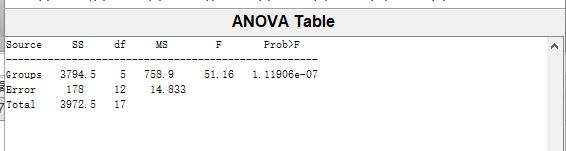
 从箱线图可以看到第2个第五个离盒子中心线较远,效果较为突出
从箱线图可以看到第2个第五个离盒子中心线较远,效果较为突出
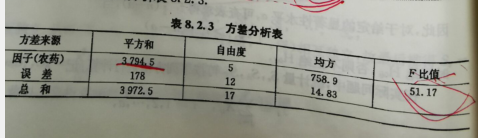
按计算公式计算得

close all;clear all;clc x1=[87,85,80];x2=[90,88,87,94];x3=[56,62];x4=[55,48];x5=[92,99,95,91];x6=[75,72,81];X=[x1,x2,x3,x4,x5,x6];ni=[length(x1),length(x2),length(x3),length(x4),length(x5),length(x6)];
% length(X)ti=[sum(x1),sum(x2),sum(x3),sum(x4),sum(x5),sum(x6)]; q1=sum(ti);a=6;n=length(X);q2=sum(X.^2);st=q2-q1^2/n;sa=sum(ti.^2./ni)-q1^2/n;se=st-sa;



p214 8
close all;clear all;clc x=[21.8,21.9,21.7,21.6,21.7,21.7,21.4,21.5,21.4,22.9,22.8,22.8,22.6,22.5,21.9,21.7,21.8,21.4];group=[ones(1,5),2*ones(1,4),3*ones(1,5),4*ones(1,4)];[p,table,stats]=anova1(x,group)p =5.4118e-08table =4×6 cell 数组'Source' 'SS' 'df' 'MS' 'F' 'Prob>F' 'Groups' [4.2450] [ 3] [1.4150] [55.0278] [5.4118e-08]'Error' [0.3600] [14] [0.0257] [] []'Total' [4.6050] [17] [] [] []stats = 包含以下字段的 struct:gnames: {4×1 cell}n: [5 4 5 4]source: 'anova1'means: [21.7400 21.5000 22.7200 21.7000]df: 14s: 0.1604


d=multcompare(stats)d =组序号' '组序号' '置信下限' '置信上限' '组均值差' '置信上限' 1.0000 2.0000 -0.0727 0.2400 0.5527 0.16261.0000 3.0000 -1.2748 -0.9800 -0.6852 0.00001.0000 4.0000 -0.2727 0.0400 0.3527 0.98172.0000 3.0000 -1.5327 -1.2200 -0.9073 0.00002.0000 4.0000 -0.5296 -0.2000 0.1296 0.33003.0000 4.0000 0.7073 1.0200 1.3327 0.0000可以看出第三组和第四组 【0.7073,1.0200】区间不包括0,说明在显著性水平0.05下,两组间均值的差异是显著的
这篇文章也介绍的很详细https://blog.csdn.net/matlab_matlab/article/details/57076854




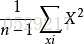







![[Data structure]队列环形队列 | 一文带你彻底搞懂队列和环形队列(内附详细图解和代码实现)](https://img-blog.csdnimg.cn/ad5f6b44b497461a8ad9fbb0f5b828b5.png)