文章目录
- 创建IP/CIDR不覆盖的VPC
- 创建VPC
- 创建子网
- 创建密钥对
- 创建EC2
- 创建Peering
- 接受Peering邀请
- 修改各个VPC的路由表
- 修改美东us-east-1 pulic subnet的路由
- 修改悉尼ap-southeast-2路由
- 测试
- 知识点
我们回顾下《AWS攻略——VPC初识》中的知识:
- 一个VPC只能设置在一个Region下。
- 一个Region可以配置多个VPC。
- 一个Region有多个Available Zone。
- 一个Subnet只能设置在一个Available Zone中。
- 一个Available Zone可以有多个Subnet。
在全球化部署的场景下,往往会出现不同Region要相互通信,这就意味着不同VPC之间要相互通信。在不增加任何措施的情况下,VPC只能通过暴露在互联网上的地址通信,但是互联网存在带宽限制、安全性和稳定性等问题。为了解决这些问题,AWS提供了Peering(对等连接)设施。Peering走的是AWS自己搭建的网络,不走因特网,于是在安全性和稳定性这块得到保证,而其带宽号称无限制(我们实测可以达到几十兆每秒)。
创建IP/CIDR不覆盖的VPC
在《AWS攻略——创建VPC》中我们创建的IP/CIDR是100.0.0.0/24,其地址区间是100.0.0.0~100.0.0.255。我们只要创建的VPC不和这个区间有重合就好。
为了体现Peering的能力,我们将在亚太地区 (悉尼)ap-southeast-2创建新的VPC,并让它和之前在美国东部 (弗吉尼亚北部)us-east-1的VPC连接。
创建VPC
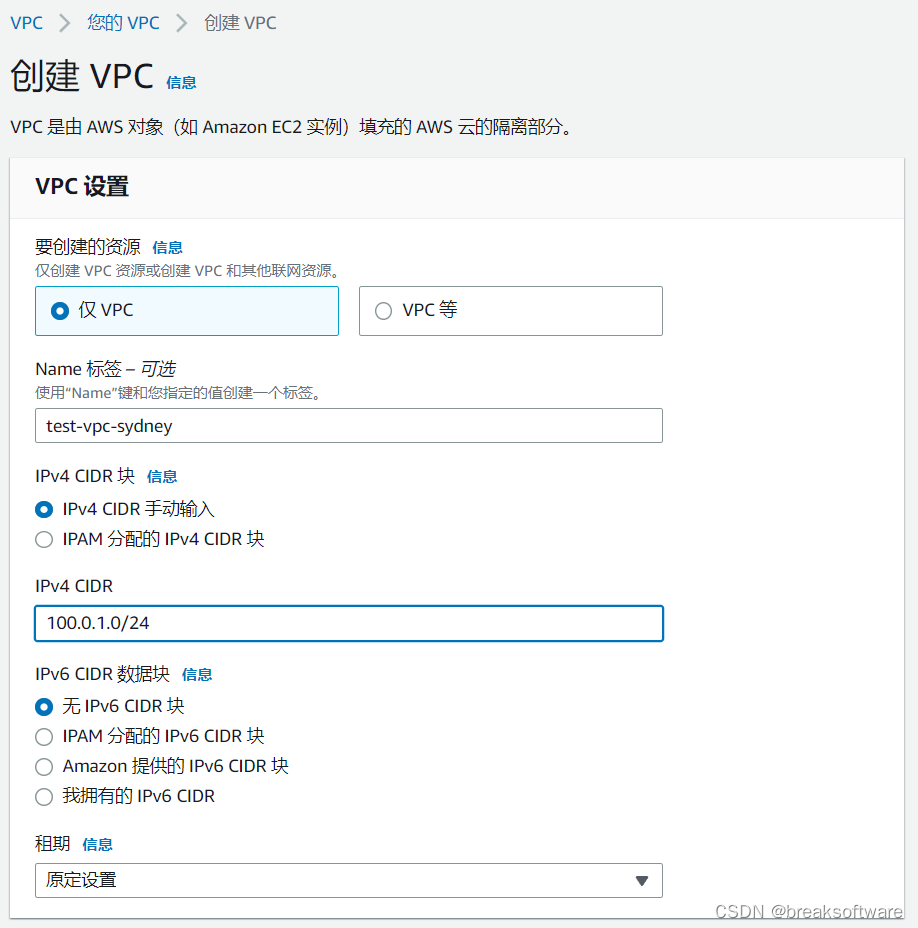
作为测试,我们将在该VPC创建一个Private Subnet,并在其中部署一台EC2。这样就可以确保我们无法通过互联网访问到这个实例。
创建子网
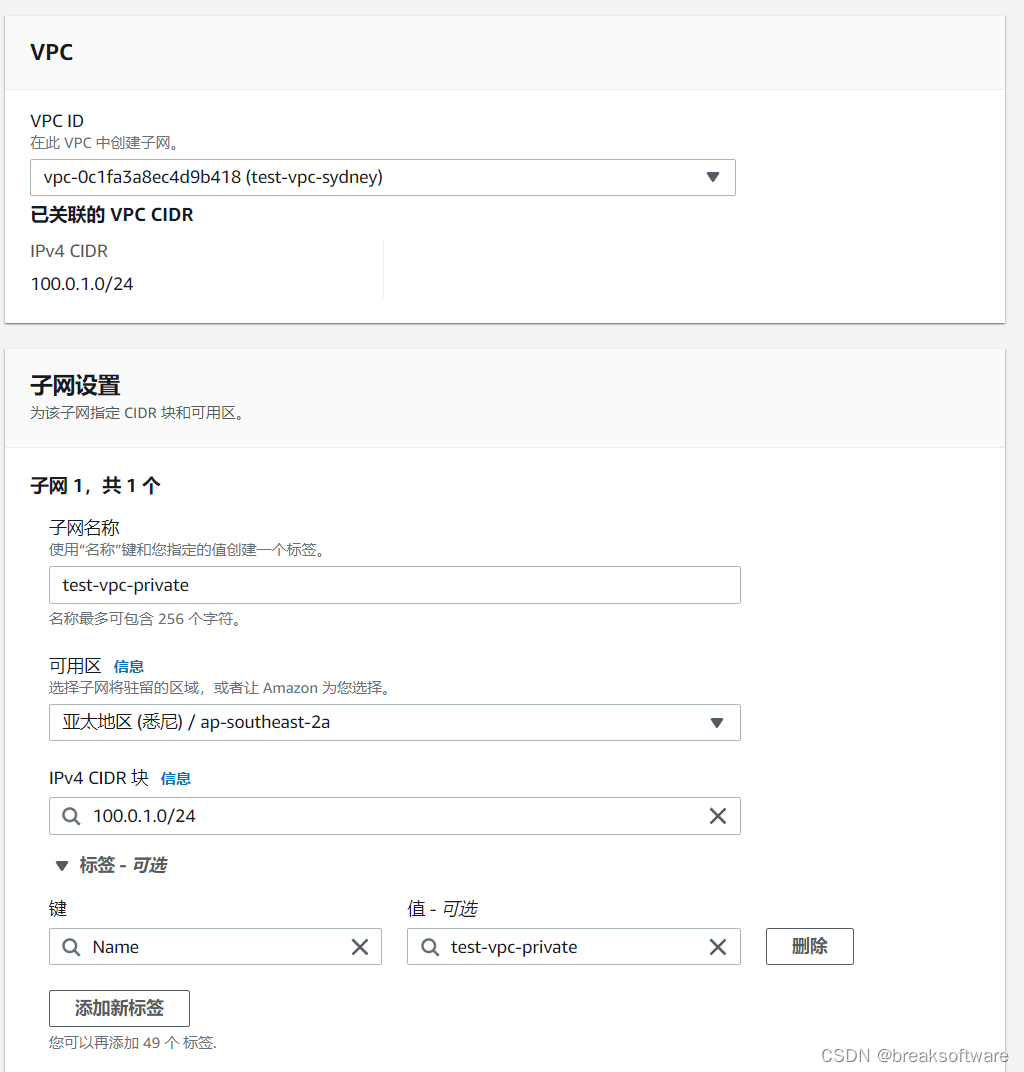
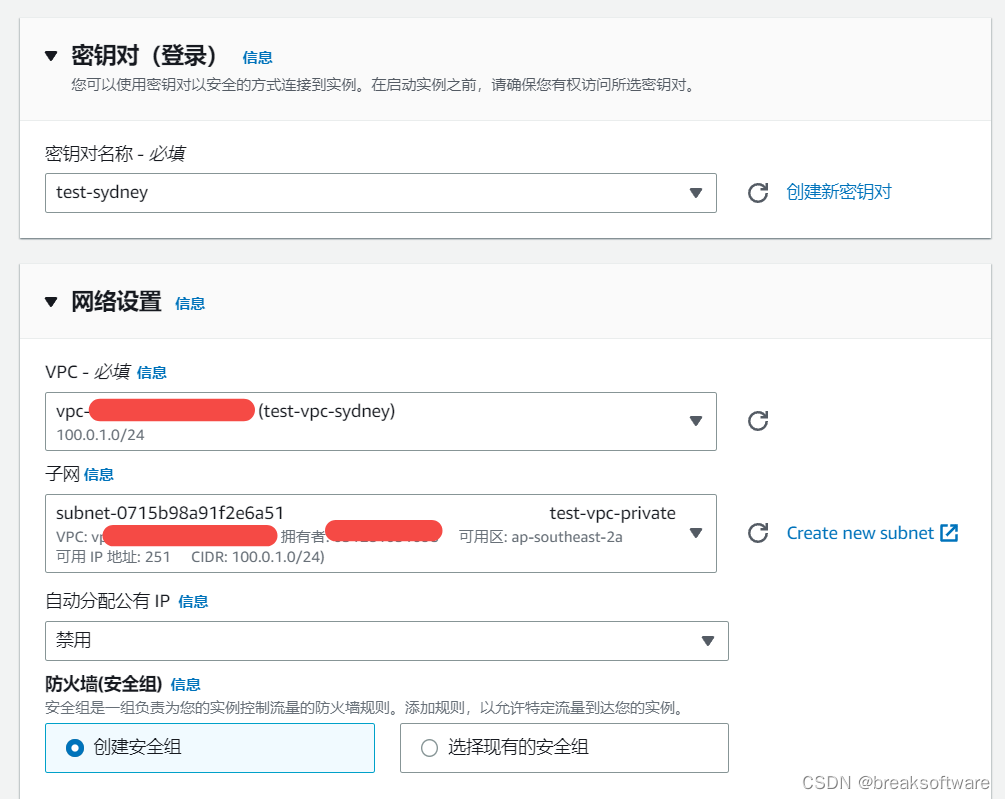
创建密钥对
记得保存这步生成的pem文件,后续要用到。
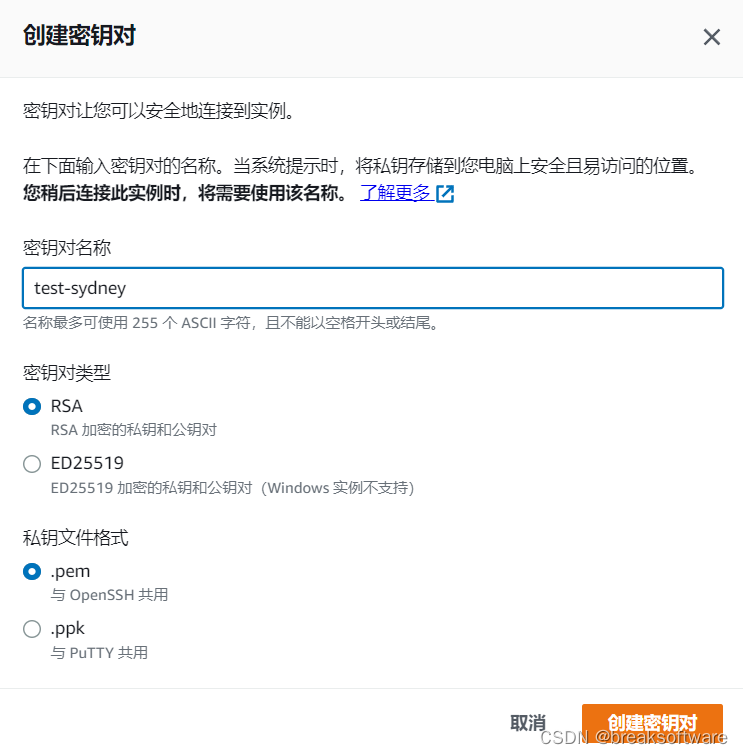
创建EC2
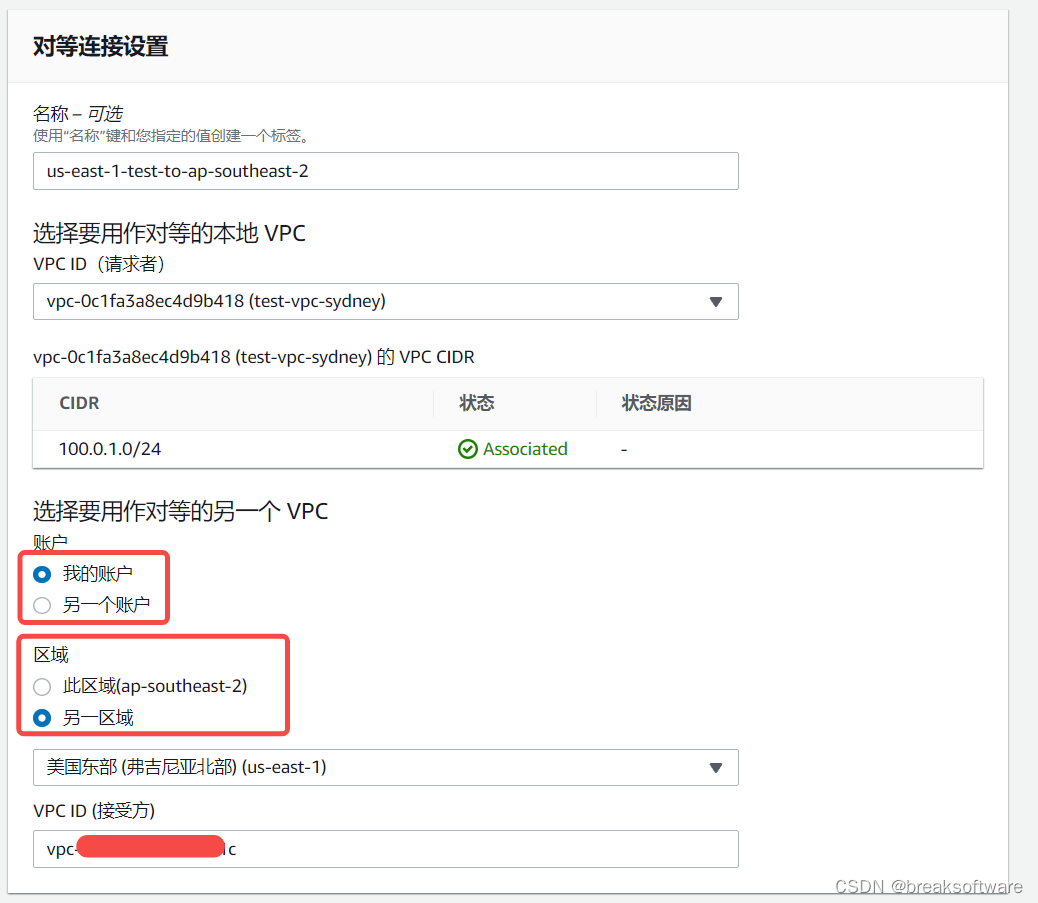
创建Peering
在创建页面中,我们选择我们账号另外一个区域(美东us-east-1)下的VPC。这儿需要将该ID复制过来。
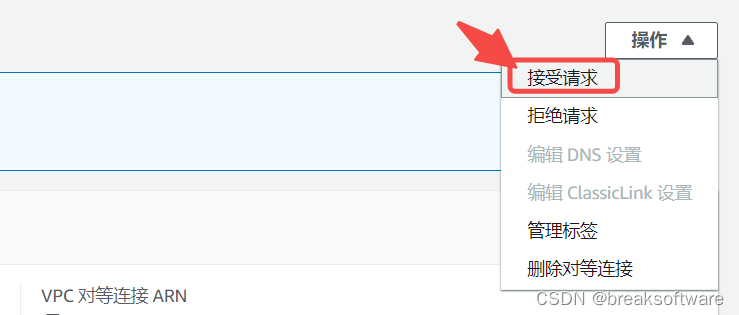
接受Peering邀请
在Peering页面,切换到弗吉尼亚区域。可以看到

点击进入后,接受该邀请。
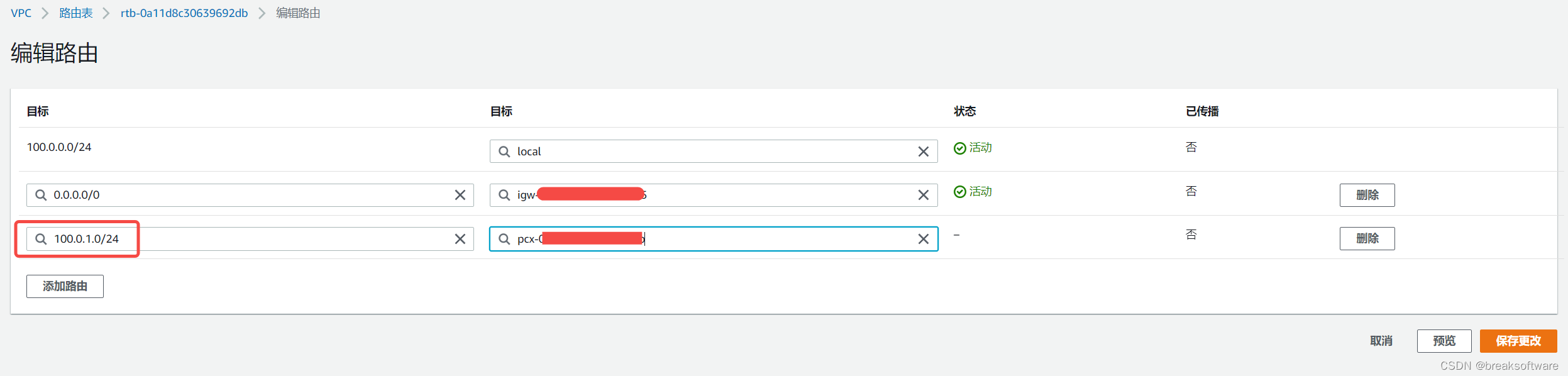
修改各个VPC的路由表
修改美东us-east-1 pulic subnet的路由
新增悉尼VPC的IP/CIDR到对等连接的路由项。
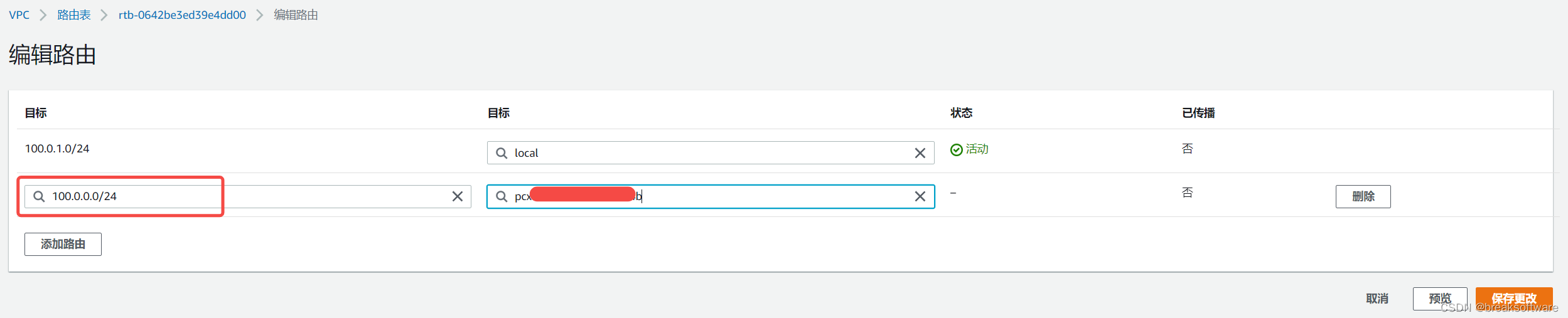
修改悉尼ap-southeast-2路由
新增弗吉尼亚VPC的IP/CIDR到对等连接的路由项。
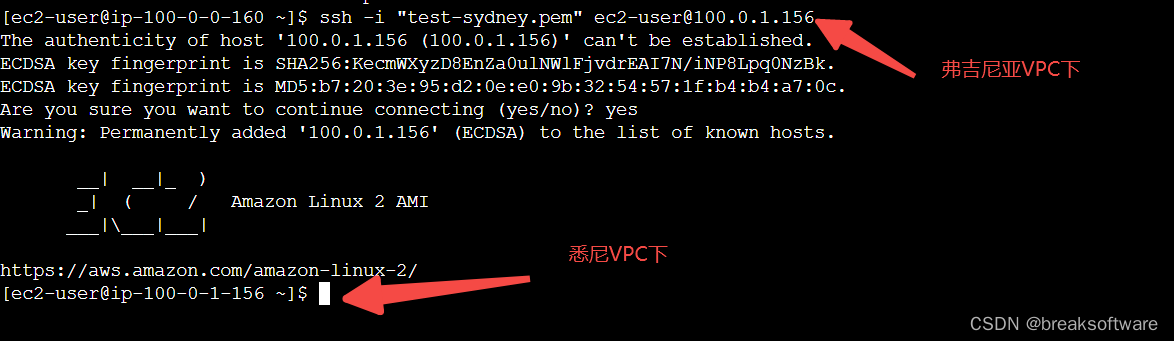
测试
知识点
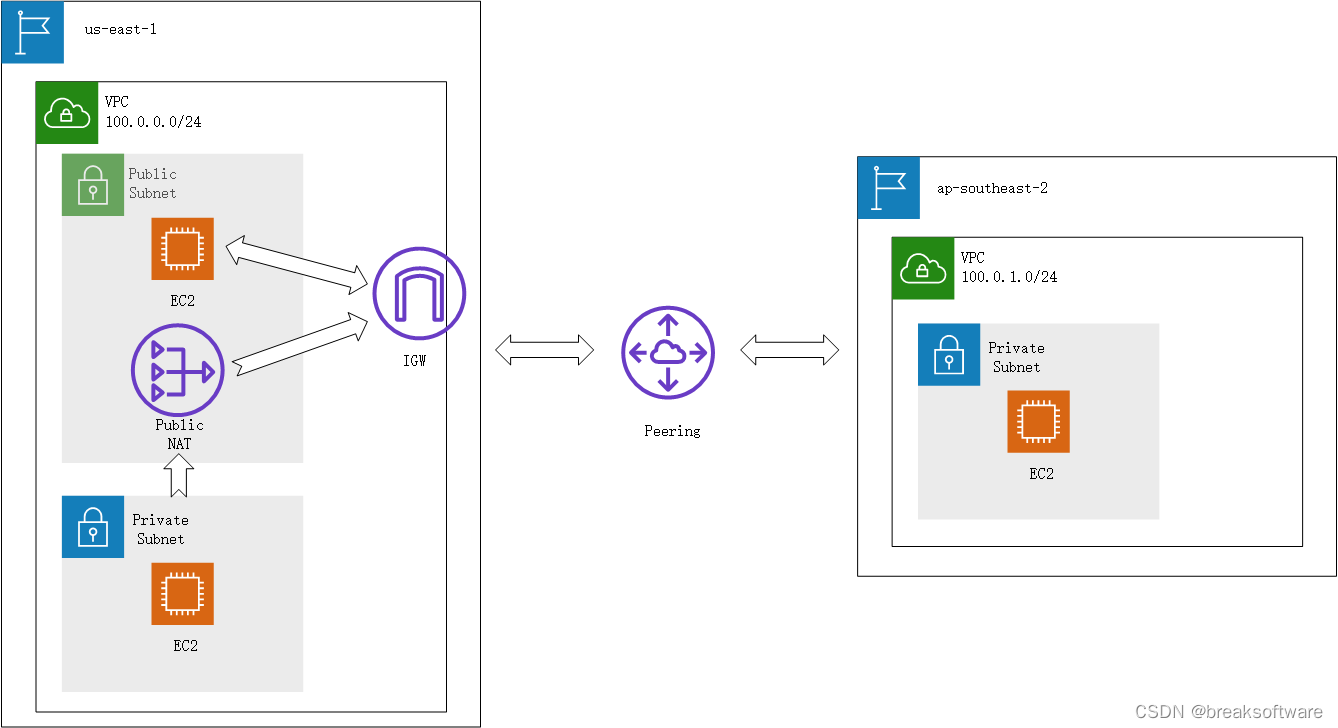
- VPC 对等连接(Peering)是两个 VPC 之间的网络连接,通过此连接,您可以使用私有 IPv4 地址或 IPv6 地址在两个 VPC 之间路由流量。这两个 VPC 中的实例可以彼此通信,就像它们在同一网络中一样。
- VPC 对等连接(Peering)可以连接:
- 相同账号的不同区域(Region)下的VPC
- 相同账号的相同区域(Region)下不同的VPC
- 不同账号的不同区域(Region)下的VPC
- 不同账号的相同区域(Region)下不同的VPC