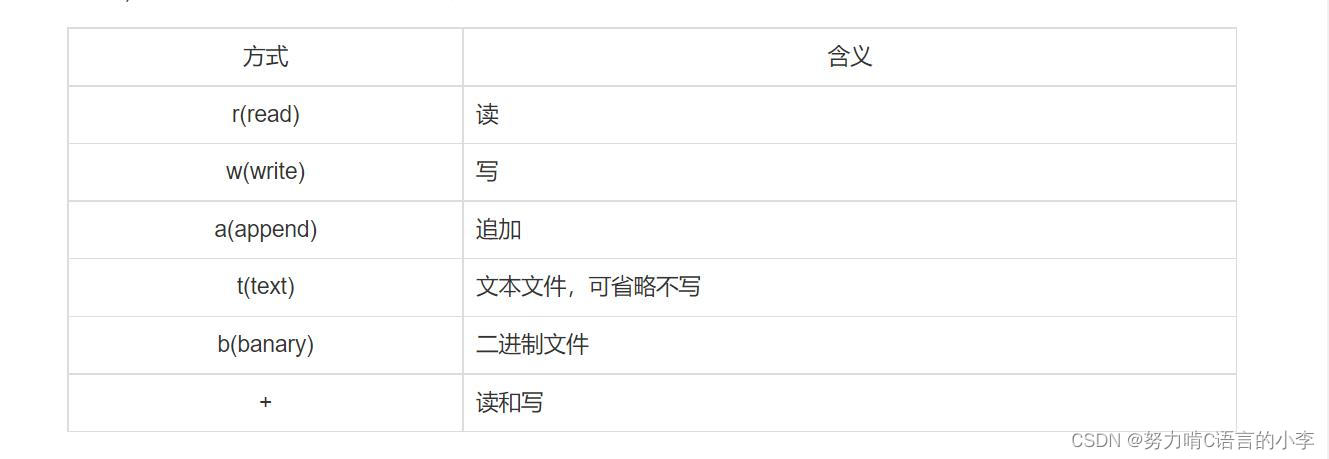
一、蒙特卡洛法介绍
蒙特·卡罗方法(Monte Carlo method),也称统计模拟方法,是一种以概率统计理论为基础的数值计算方法,常用于特定条件下的概率计算问题。蒙特卡罗是摩纳哥的著名赌城,该法为表明其随机抽样的本质而命名。
算法思路简单也好理解:比如抛一枚硬币,假设我们开始不知道正面朝上的概率是多少,却有大量的时间来将硬币抛一万次,那么在一万次试验后,会发现正面朝上的次数接近一半,当然,抛的次数越多,概率越接近50%,蒙特卡洛方法是大数定律在实际应用问题上的体现。其优点十分明显,基本可以绕开问题本身的“黑盒”,不必考虑问题内部的结构而只关注问题的输入与输出,利用输出的结果来分析问题,适用于对离散系统进行计算仿真试验。
例如上例中,我们不用考虑硬币在空中停留多长时间,不用考虑抛出力度、硬币大小、空气阻力、风速等乱七八糟的问题,在大量的试验后只关注最后硬币哪面朝上,就能正确估算出硬币正面朝上的概率。同样的,例如我们不知道走到某个路口需要等红绿灯的概率,不知道某个产品线的合格率,蒙特卡洛法告诉你:模拟一万次试验后你就知道了O(∩_∩)O~
二、利用蒙特卡洛方法计算圆周率π
采用蒙特卡洛思想,首先在一个正方形区域内随机生成若干个均匀分布的点,随后判断哪些点在正方形的内切圆范围内。如果点的数量足够多,那么圆内点的数量与点的总数量的比值,就是圆的面积与正方形面积之比。利用点数量的比值与正方形面积就可以推出圆的面积,进而得出圆周率π。
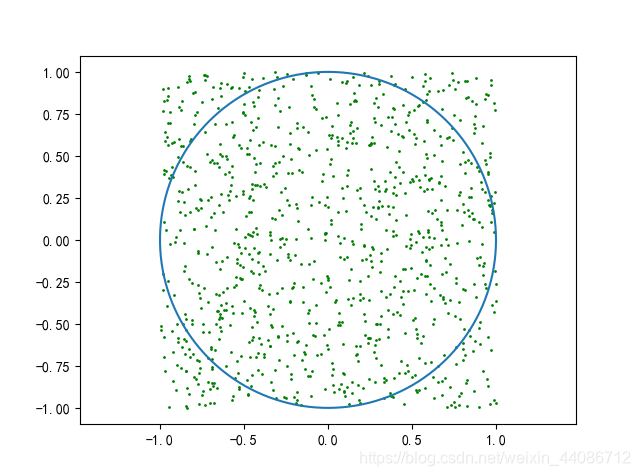
上代码:
import numpy as np
import matplotlib.pyplot as plt
import math
from tqdm import tqdm
from numpy import meancenter_x = 0.0 #圆心横坐标
center_y = 0.0 #圆心纵坐标
r = 1.0 #半径class Caculate_Pi:def __init__(self,dot_num):self.dot_num = dot_num #初始化点的数量self.count = 0 #圆内点的计数器self.x = np.random.uniform(center_x - r,center_x + r,self.dot_num) #点均匀分布的横轴范围self.y = np.random.uniform(center_y - r,center_y + r,self.dot_num) #点均匀分布的纵轴范围def Judge(self,x,y,r): #判断点是否在圆内return np.sqrt(x ** 2 + y ** 2) <= rdef Count(self): #计算圆内点的个数result = [self.Judge(self.x[i], self.y[i], r) for i in range(self.dot_num)]for i in result:if i:self.count += 1dot_num = []
Pi = []
for i in tqdm(range(1,1000)): #考虑从100到1000000个点模拟的π值如何变化dot_num.append(100 * i)demo = Caculate_Pi(100 *i)demo.Count()pi = demo.count * 4 /(100 * i)Pi.append(pi)
#可视化随着点数量增多模拟π的变化
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.xlabel('模拟次数')
plt.ylabel('模拟的Pi值')
plt.axhline(y = math.pi,c = "red")
plt.annotate('y=π',xy=(0,3.1415926),xytext=(-8000,3.14))
plt.plot(dot_num,Pi)
print('模拟得到的π均值:',mean(Pi[100:]))
运行结果:

可以看出模拟次数越多(从100到100000),模拟的π值越来越趋近于真实的π(3.141592654)。本次计算最终模拟的平均值为
模拟得到的π均值:3.1414679762608873
已经比较接近了,以上就是利用蒙特卡洛法计算圆周率的小练习。
当然,计算的方法还包括经典的精确算法——割圆法、无穷级数法,其同样可以用代码实现,下次无聊的时候再写吧。