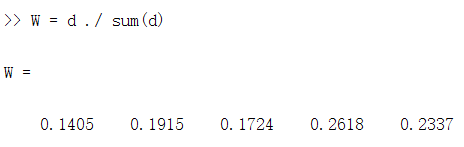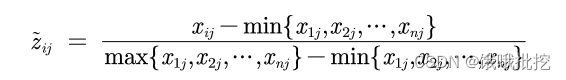解决问题

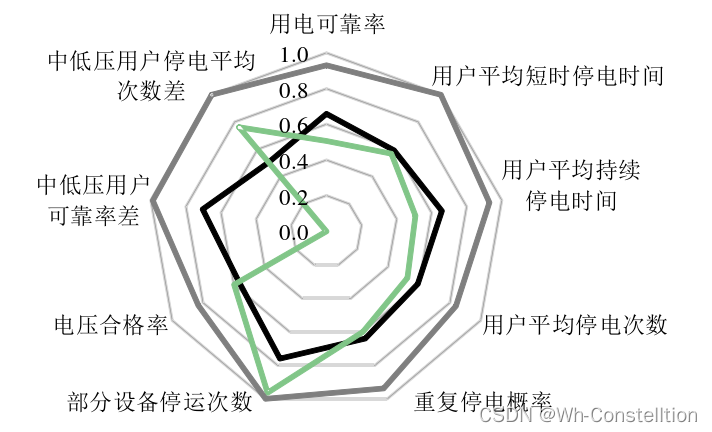
建模比赛中最基础的模型之一，其主要用于解决评价类问题（例如：选择哪种方案最好、哪位运动员或者员工表现的更优秀），用于确定每个指标所占权重，权重用于计算最终得分。

优点

层次分析法最大的缺点在于判断矩阵的确定依赖于专家，如果专家的判断存在主观性的话，会对结果产生很大的影响。

熵权法是一种客观赋权方法，它依据的原理是：指标的变异程度越小，所反映的信息量也越少，其对应的权值也应该越低（客观= 数据本身就可以告诉我们权重）。

缺点

因为概率p是位于0‐1之间，因此需要对原始数据进行标准化，我们应该选择哪种方式进行标准化呢？查看知网的文献会发现，并没有约定俗成的标准，每个人的选取可能都不一样。但是不同方式标准化得到的结果可能有很大差异，所以说熵权法也存在着一定的问题。

一般步骤

1. 判断输入的矩阵中是否存在负数，如果有则要重新标准化到非负区间（后面计算概率时需要保证每一个元素为非负数）

在这里插入图片描述
数据正向化过程请参考文章:
数学建模常用算法—优劣解距离法(TOPSIS)
https://blog.csdn.net/cyj972628089/article/details/107541291

2. 计算第j项指标下第i个样本所占的比重，并将其看作相对熵计算中用到的概率

在这里插入图片描述

3. 计算每个指标的信息熵，并计算信息效用值，并归一化得到每个指标的熵权

在这里插入图片描述

代码

	Z = [];	 % n*m的矩阵（要经过正向化和标准化处理，且元素中不存在负数）[n,m] = size(Z);D = zeros(1,m);  % 初始化保存信息效用值的行向量for i = 1:mx = Z(:,i);  % 取出第i列的指标p = x / sum(x);% 注意，p有可能为0，此时计算ln(p)*p时，Matlab会返回NaN，所以这里我们自己定义一个函数e = -sum(p .* mylog(p)) / log(n); % 计算信息熵D(i) = 1- e; % 计算信息效用值endW = D ./ sum(D);  % 将信息效用值归一化，得到权重    
end

function [lnp] =  mylog(p)
n = length(p);   % 向量的长度
lnp = zeros(n,1);   % 初始化最后的结果for i = 1:n   % 开始循环if p(i) == 0   % 如果第i个元素为0lnp(i) = 0;  % 那么返回的第i个结果也为0elselnp(i) = log(p(i));  endend
end