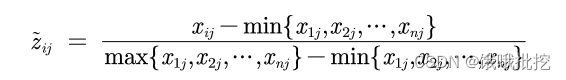数学建模系列---熵权法

article/2025/11/10 12:10:22

一.简介

二.说明

1.正向指标：

2.信息量

3.信息熵

三.具体计算步骤

1.标准化矩阵

1.1该步骤的意义

1.2标准化的2种方法

2.计算各元素概率

3.计算各指标的权重

3.1计算每个指标的信息熵

3.2计算信息效用值

3.3归一化信息效用值

四.总结

一.简介

熵权法是对指标体系客观（利用已知数据）赋权的方法。

原理如下：

指标的变异程度（方差）越小，所反映的信息量也越少（同时信息熵越大），其对应的权值也应该越低。

直白一点来说：越可能发生的事信息熵越大，信息量越少，权值也越低

通过一个例子理解熵权法原理

NBA要对5名球星：科比、詹姆斯、哈登、巴特勒、杜兰特进行综合实力评估。评估的指标体系是：三分命中率罚球命中率场均助攻数场均失误数场均得分数。即用这5个指标来综合评估球员实力，虚拟数据如下：

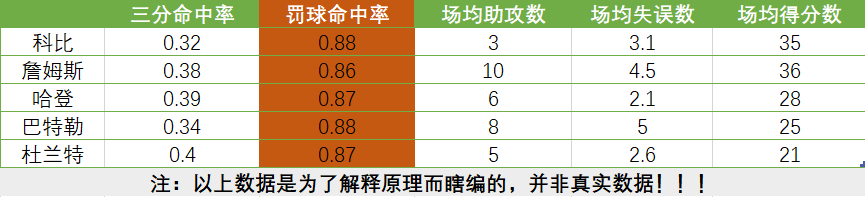
根据已知数据对球员打分，关键问题在于如何对5个指标赋权，从上表数据可知：球员们的罚球命中率旗鼓相当，即我们可以认为这个事实<罚球命中率在0.88左右>发生的可能性很大，根据这个指标的数据我们可以得到的信息很少，但是通过场均助攻数该指标数据，我们可以得到的信息就相对很多了，引入原理：罚球命中率该指标的变异程度较小，所反映的信息很少、信息熵很大，那么相应的权重就应越低。

二.说明

在本文的第三部分计算权值时会用到以下几个知识点，大家可以先学习一下。

1.正向指标：

指标值越大，则评价就越好。与此相对的是负向指标。

举例：场均得分----越大越好----正向指标，场均失误----越小越好----负向指标。

2.信息量

计算公式：I（x）=-ln(p(x))

公式推导：

利用我们之前提到的<越有可能发生的事情包含的信息量越小>这一原理

将信息量用字母I表示，概率用p表示，那么我们可以将它们建立一个函数关系：

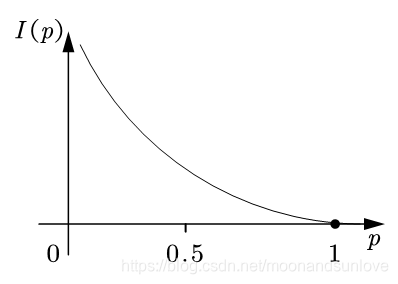
假设 x 表示事件 X 可能发生的某种情况，p(x)表示该事件发生的概率，那么 $I(p)=-ln(p(x))$ ，因为 $0\leqslant p(x)\leqslant 1$ ，所以 $I(x)\geqslant 0$ 。

说明：此处的 $I(p)=-ln(p(x))$ ,其中的对数是以e为下标的，也可将2作为下标，对此，目前没有统一要求。

对信息量的推导感兴趣的朋友可以看这边文章：什么是信息量？如何计算信息量？ - 知乎 (zhihu.com)

3.信息熵

概念：信息量度量的是一个具体事件发生了所带来的信息，而熵则是在结果出来之前对可能产生的信息量的期望—考虑该随机变量的所有可能取值，即所有可能发生事件所带来的信息量的期望。 -----知乎用户：忆臻

事件X的信息熵H(X)如下:

$H(X)=\sum_{i=1}^{n}\left[p\left(x_{i}\right) I\left(x_{i}\right)\right]=-\sum_{i=1}^{n}\left[p\left(x_{i}\right) \ln \left(p\left(x_{i}\right)\right)\right]$

从公式也可以看出，信息熵本质上就是对信息量的期望，且式中唯一的未知数是事件x的概率。

三.具体计算步骤

1.标准化矩阵

1.1该步骤的意义

对已知数据进行去量纲化，使得各指标在同一量纲。ps:标准化处理方法是去量纲化的其中一种方法。避免负值数据，为下一步<计算各元素的概率>做准备，因为概率是恒大于0的。

1.2标准化的2种方法

假设有n个要评价的对象，m个评价指标（已经正向化了）构成的矩阵如下：X经过标准化处理后的矩阵为Z。

$X=\left[\begin{array}{cccc} x_{11} & x_{12} & \cdots & x_{1 m} \\ x_{21} & x_{22} & \cdots & x_{2 m} \\ \vdots & \vdots & \ddots & \vdots \\ x_{n 1} & x_{n 2} & \cdots & x_{n m} \end{array}\right]$

法1：当矩阵X中不存在负值时才可以使用，例如前面的球员数据表就无负值数据。

$z_{i j}=x_{i j} / \sqrt{\sum_{i=1}^{n} x_{i j}^{2}}$

法2：当矩阵X中存在负值时使用

${z}_{i j}=\frac{x_{i j}-\min \left\{x_{1 j}, x_{2 j}, \cdots, x_{n j}\right\}}{\max \left\{x_{1 j}, x_{2 j}, \cdots, x_{n j}\right\}-\min \left\{x_{1 j}, x_{2 j}, \cdots, x_{n j}\right\}}$

2.计算各元素概率

通过上一步的处理，我们得到了矩阵Z

$Z=\left[\begin{array}{cccc} z_{11} & z_{12} & \cdots & z_{1 m} \\ z_{21} & z_{22} & \cdots & z_{2 m} \\ \vdots & \vdots & \ddots & \vdots \\ z_{n 1} & z_{n 2} & \cdots & z_{n m} \end{array}\right]$

现在计算第j项指标下第i个样本所占的比重，并将其看作熵计算中用到的概率。可以得到一个概率矩阵P，P中每一个元素 $p_{i j}$ 的计算公式如下：

$p_{i j}=\frac{{z}_{i j}}{\sum_{i=1}^{n} {z}_{i j}}$

计算原理很简单：该元素/该列元素之和，以球员数据表为例：

$p_{11}=\frac{0.32}{0.32+0.38+0.39+0.34+0.4}=0.175$

3.计算各指标的权重

流程图如下：

3.1计算每个指标的信息熵

对于第j个指标而言，其信息熵的计算公式为

$e_{j}=-\frac{1}{\ln n} \sum_{i=1}^{n} p_{i j} \ln \left(p_{i j}\right)(j=1,2, \cdots, m)$

说明：

1>为什么要除 $\ln n$ ?

因为当 $p\left(x_{1}\right)=p\left(x_{2}\right)=\cdots=p\left(x_{n}\right)=\frac{1}{n} \text,$ 时，H(X)有最大值 $\ln n$ ,那么除以 $\ln n$ 就可以使信息熵的值始终落在[0,1]区间上。

2> $e_{j}$ 越大，第j个指标的信息就越少。