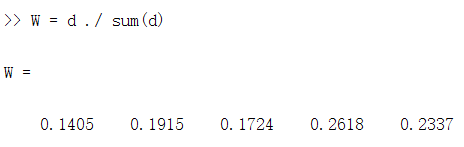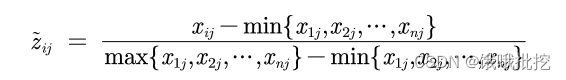Topsis法（Technique for Order Preference by Similarity to Ideal Solution）可翻译为逼近理想解排序法，国内常简称为优劣解距离法。

Topsis法是一种常用的综合评价方法，其能充分利用原始数据的信息，其结果能精确地反映各评价方案之间的差距。

在之前，我们学习过层次分析法（AHP）。其中，层次分析法模型的局限性是需要我们构造判断矩阵，这具有很强的主观性，并且决策因子数量最好不超过10个。那么有没有一种客观的方法去判断各因子之间的权重呢？基于熵权法的Topsis模型可以解决这个问题。

本文借鉴了数学建模清风老师的课件与思路，如果大家发现文章中有不正确的地方，欢迎大家在评论区留言，也可以点击查看右侧链接查看清风老师视频讲解：【强烈推荐】清风：数学建模算法、编程和写作培训的视频课程以及Matlab等软件教学_哔哩哔哩_bilibili

一个小例子引出Topsis模型

这样评分有不合理之处，若小王得分为10分，那么他的总评分还是为0.1分，这显然是不合理的。因此我们需要修改评价模型。

比较好的想法：

方法1

卷面最高成绩max：100

卷面最低成绩min：0

计算评分的公式： $\frac{x-0}{100-0}$

方法2

最高成绩max：99

最低成绩min：60

计算评分的公式： $\frac{x-min}{max-min}$

对于这个问题，可能大家会选方法1去进行评分，但大多是实际情况下，是没有最大值这个项的，如：国家年GDP增速等数据。并且比较的指标往往不只是单方面的，如成绩、竞赛成绩等。因此方法2更适合我们去进行评分。

拓展：增加指标个数

新增加了一个指标，现在要综合评价四位同学，并为他们进行评分

成绩是越高越好，这样的指标称为极大型指标（效益型指标）。

与他人争吵的次数是越少越好，这样的指标称为极小型指标（成本型指标）。

第一步：指标正向化

统一指标类型

将所有的指标转化为极大型称为指标正向化

极小型➡极大型

**极小型指标转换为极大型指标的公式：**max-x（此公式不唯一，若数据都为正数，那么也可以使用 $\frac{1}{x}$ ，此公式合理即可）

中间型➡极大型

中间型指标：指标值既不要太大也不要太小，取某特定值最好（如水质量评估 PH 值）。是一组中间型指标序列，且最佳的数据为，那么正向化的公式如下：

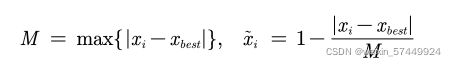
因此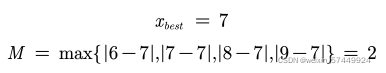

区间型➡极大型

区间型指标：指标值落在某个区间内最好，例如人的体温在36°～37°这个区间比较好。

第一步代码展示

[n,m] = size(X);
disp(['共有' num2str(n) '个评价对象, ' num2str(m) '个评价指标']) 
Judge = input(['这' num2str(m) '个指标是否需要经过正向化处理，需要请输入1 ，不需要输入0：  ']);if Judge == 1Position = input('请输入需要正向化处理的指标所在的列，例如第2、3、6三列需要处理，那么你需要输入[2,3,6]： '); disp('请输入需要处理的这些列的指标类型（1：极小型， 2：中间型， 3：区间型） ')Type = input('例如：第2列是极小型，第3列是区间型，第6列是中间型，就输入[1,3,2]：  '); for i = 1 : size(Position,2) X(:,Position(i)) = Positivization(X(:,Position(i)),Type(i),Position(i));enddisp('正向化后的矩阵 X =  ')disp(X)
end

第二步：正向化矩阵标准化

标准化的目的就是消除不同量纲的影响。

假设有n个要评价的对象，m个评价指标（已经正向化了）构成的正向化矩阵如下：

那么对其标准化后的矩阵记为Z，Z的每一个元素：

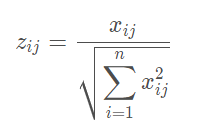
即得到标准化矩阵Z（每一个元素/根号下所在列元素的平方和）:

注意：标准化的方法不唯一，但目的都是为了去量纲。

那么对题目中的矩阵进行处理：

第二步代码展示

Z = X ./ repmat(sum(X.*X) .^ 0.5, n, 1);
disp('标准化矩阵 Z = ')
disp(Z)

第三步：计算得分并归一化

定义最大值：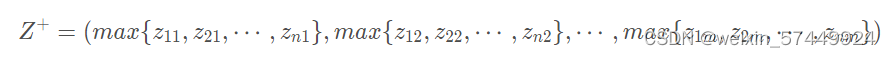

定义最小值：

定义第i（i = 1,2,…,n）个评价对象与最大值的距离：

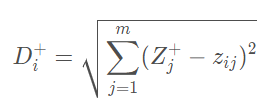
定义第i（i = 1,2,…,n）个评价对象与最小值的距离：

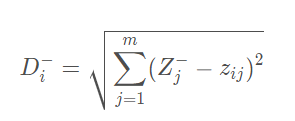
那么，我们可以计算得出第 i( i = 1,2,…,n) 个评价对象未归一化的得分:

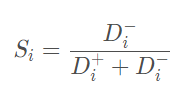
很明显 0≤Si≤1，且 Si 越大 Di+ 越小，即越接近最大值。

得分结果如下

第三问代码展示

D_P = sum([(Z - repmat(max(Z),n,1)) .^ 2 ],2) .^ 0.5;
D_N = sum([(Z - repmat(min(Z),n,1)) .^ 2 ],2) .^ 0.5; 
S = D_N ./ (D_P+D_N);   
disp('最后的得分为：')
stand_S = S / sum(S)
[sorted_S,index] = sort(stand_S ,'descend')

模型拓展

熵权法

信息量

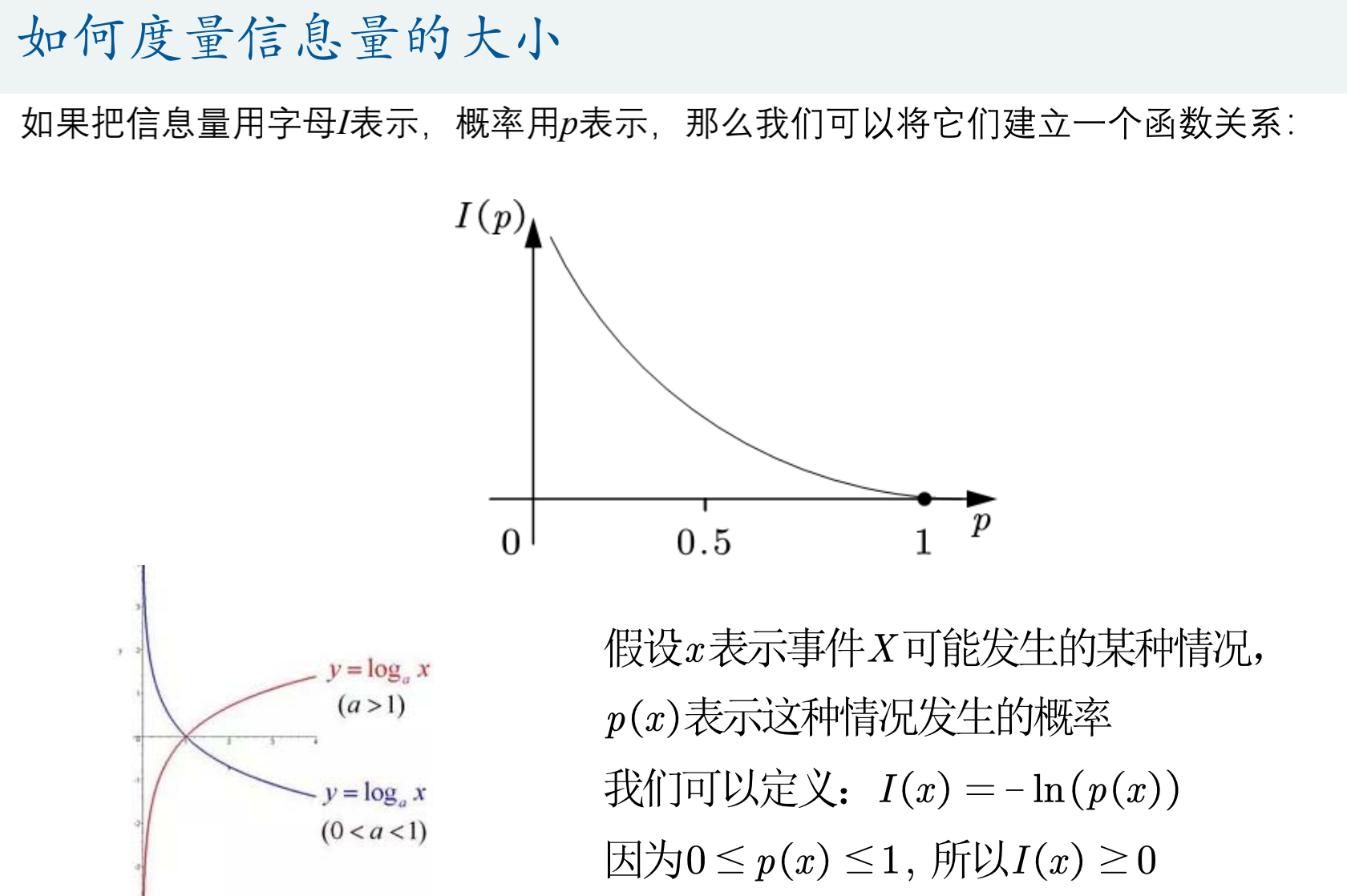
信息熵

事件所有发生情况的概率相等时，信息熵取最大值（只需要知道，不需要证明）

熵越大信息量越大还是越小？

对于熵权法而言，因为我们关注的是已有的信息，所以答案是越小（后面大家看到计
算步骤就会明白）

计算步骤

对正向化的矩阵进行标准化，

如果有非负数，则采用标准化方式：（xij-该列最小值）/（该列最大值-该列最小值）

计算每一列（每一个指标）中每个元素所占比重，看作计算相对熵时要用到的概率

标准化后的矩阵

pij= zij/所在列的和

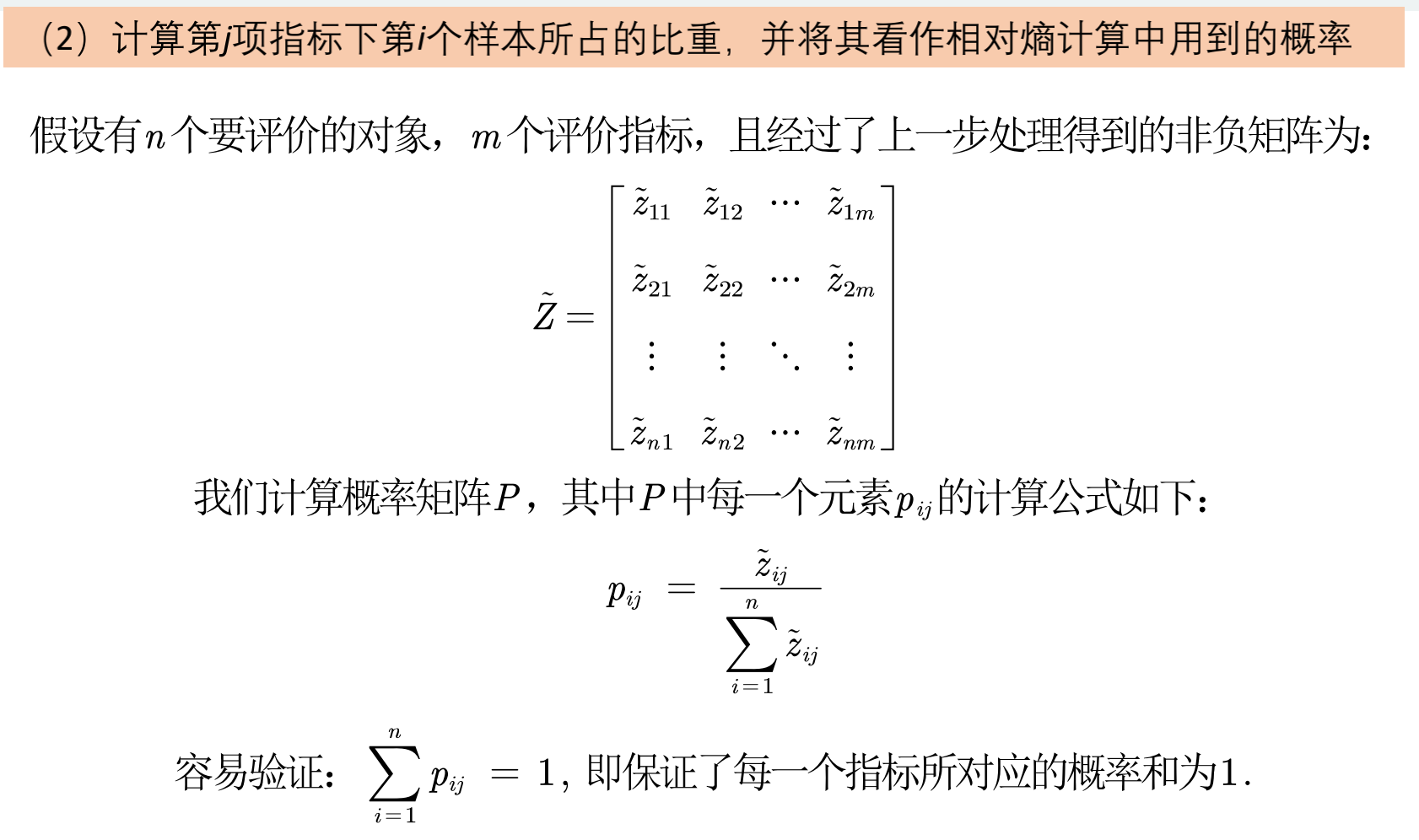
（这种求法有待商榷，但是大家都这么用）

计算每个指标信息熵

两个小问题的说明

除lnn，使信息熵ej落在[0,1]之间。因为信息熵越大，所含信息越小。
所以用1-ej来表示信息效用值，效用值越大，所含信息越多

将信息效用进行归一化

背后原理

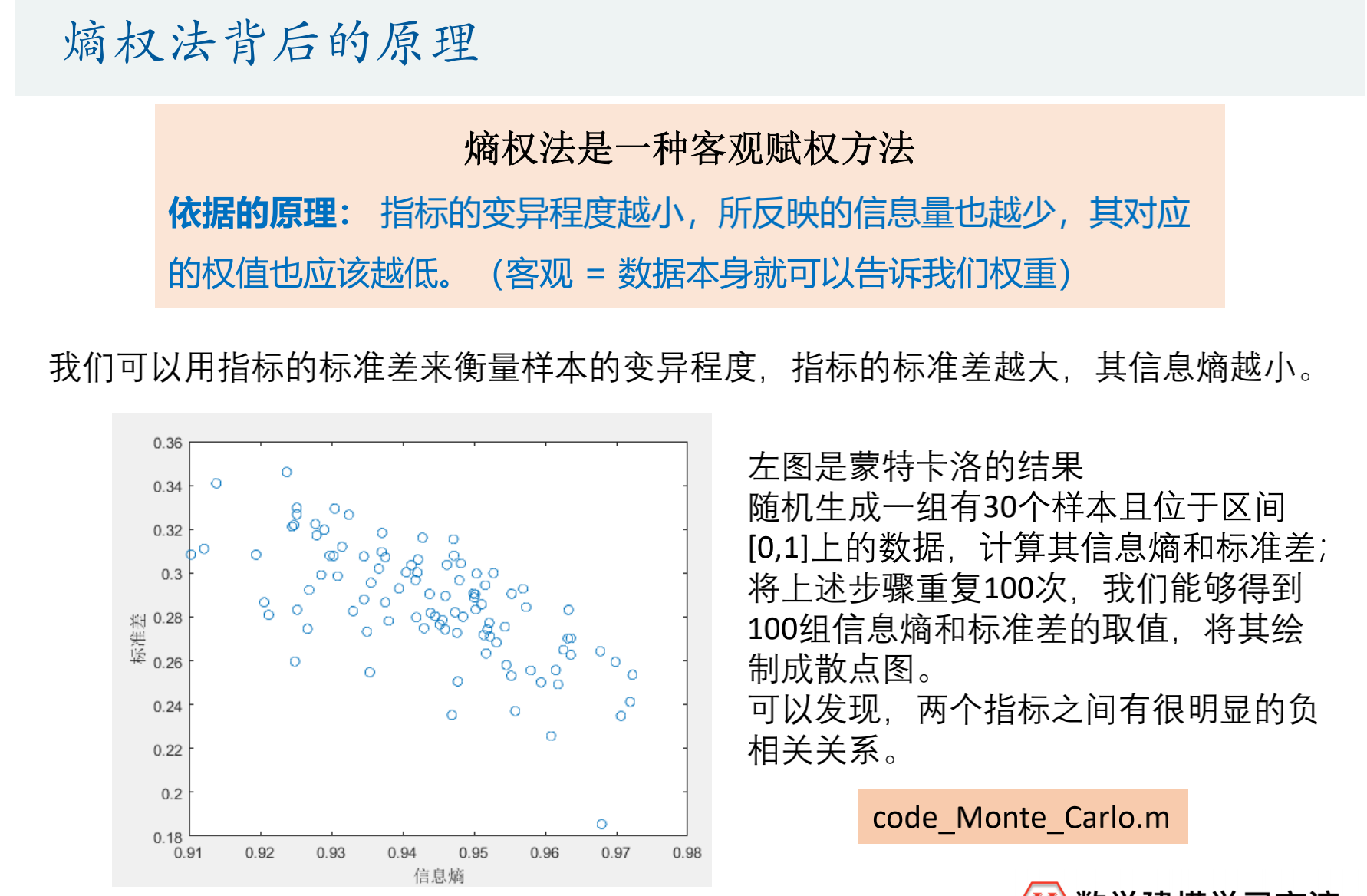
问题

基于熵权法的Topsis模型：

我们在上面讨论时，有一个问题没有考虑，就是两个指标之间的权重关系，因为层次分析法是一个比较主观的计算权重方法，在这里会介绍一个客观的求权重方法：熵权法

熵权法的原理是指标的变异程度越小，所反映的信息量也越少，其对应的权值也应该越低。因此数据本身就告诉了我们权重。所以说熵权法是一种客观的方法。但就如评价三好学生的例子，只有学习成绩与违纪次数去评价一个学生，使用了熵权法之后，反而违纪次数的权重近于0，显然不符合常理。因此使用此方法后我们需要人工干预，判断一下权重是否合理（如2021年国赛C283论文）。若不合理，可通过层次分析法去修正权重大小。

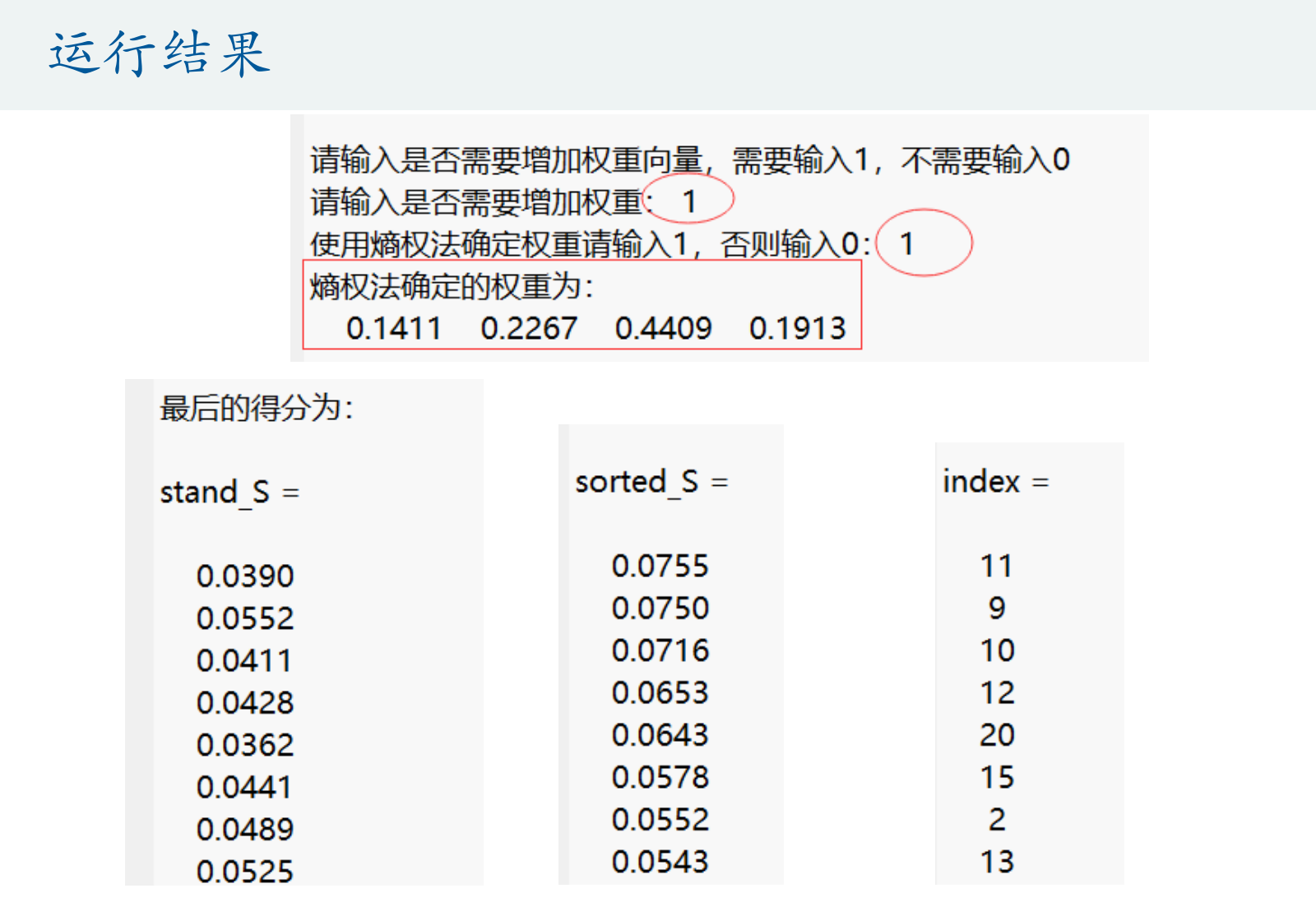
熵权法代码展示

disp("请输入是否需要增加权重向量，需要输入1，不需要输入0")
Judge = input('请输入是否需要增加权重： ');
if Judge == 1Judge = input('使用熵权法确定权重请输入1，否则输入0： ');if Judge == 1if sum(sum(Z<0)) >0   % 如果之前标准化后的Z矩阵中存在负数，则重新对X进行标准化disp('原来标准化得到的Z矩阵中存在负数，所以需要对X重新标准化')for i = 1:nfor j = 1:mZ(i,j) = [X(i,j) - min(X(:,j))] / [max(X(:,j)) - min(X(:,j))];endenddisp('X重新进行标准化得到的标准化矩阵Z为:  ')disp(Z)endweight = Entropy_Method(Z);disp('熵权法确定的权重为：')disp(weight)elsedisp(['如果你有3个指标，你就需要输入3个权重，例如它们分别为0.25,0.25,0.5, 则你需要输入[0.25,0.25,0.5]']);weight = input(['你需要输入' num2str(m) '个权数。' '请以行向量的形式输入这' num2str(m) '个权重: ']);OK = 0;  % 用来判断用户的输入格式是否正确while OK == 0 if abs(sum(weight) -1)<0.000001 && size(weight,1) == 1 && size(weight,2) == m  % 注意，Matlab中浮点数的比较要小心OK =1;elseweight = input('你输入的有误，请重新输入权重行向量: ');endendend
elseweight = ones(1,m) ./ m ; %如果不需要加权重就默认权重都相同，即都为1/m
end

模型总结

Topsis优劣解距离法模型是一种常用的综合评价方法，能充分利用原始数据的信息，其结果能精确地反映各评价方案之间的差距。相对于层次分析法而言，Topsis法是解决决策层中数据已知的评价类模型。它可以解决多数据量的题目，数据计算简单易行。但对于各数据量之间的关系，我们需要使用熵权法或层次分析法来建立权重。

熵权法的原理是指标的变异程度越小，所反映的信息量也越少，其对应的权值也应该越低。因此数据本身就告诉了我们权重。所以说熵权法是一种客观的方法。但就如评价三好学生的例子，只有学习成绩与违纪次数去评价一个学生，使用了熵权法之后，反而违纪次数的权重近于0，显然不符合常理。因此使用此方法后我们需要人工干预，判断一下权重是否合理（如2021年国赛C283论文）。综合来说，在比赛中，对于决策层中数据已知的问题，使用Topsis模型十分合适。

解题步骤：1.熵权法确定权重

1.1数据标准化

1.2求出各指标的信息熵

1.3计算各指标的差异系数

1.4确定各指标的权重

1.5分别用权重乘以归一化后的数据

2.将原始矩阵正向化（变为极大型指标）

3.正向化矩阵标准化

4.确定最优方案和最劣方案

5.计算各评价对象与最优方案、最劣方案的接近程度

6.计算各评价对象与最优方案的贴近程度

7.根据贴近程度大小进行排序，给出评价结果